assignment1SVM的一些经验

def svm_loss_vectorized(W, X, y, reg):
  """
  Structured SVM loss function, vectorized implementation.

  Inputs and outputs are the same as svm_loss_naive.
  """
  loss = 0.0e0
  dW = np.zeros(W.shape,dtype='float64') # initialize the gradient as zero

  #############################################################################
  # TODO:                                                                     #
  # Implement a vectorized version of the structured SVM loss, storing the    #
  # result in loss.                                                           #
  #############################################################################
  pass
  #############################################################################
  #                             END OF YOUR CODE                              #
  #############################################################################
  num_train = X.shape[0]
  score = np.dot(X, W)
  loss_matrix = np.maximum(0, score - score[np.arange(num_train), np.array(y)].reshape(-1, 1) + 1)
  loss_matrix[np.arange(num_train), np.array(y)] = 0
  loss = np.sum(loss_matrix)
  loss /= num_train
  loss += 0.5 * reg * np.sum(W * W)
  
  

  #############################################################################
  # TODO:                                                                     #
  # Implement a vectorized version of the gradient for the structured SVM     #
  # loss, storing the result in dW.                                           #
  #                                                                           #
  # Hint: Instead of computing the gradient from scratch, it may be easier    #
  # to reuse some of the intermediate values that you used to compute the     #
  # loss.                                                                     #
  #############################################################################
  num_classes = W.shape[1]
  coeff_mat = np.zeros((num_train, num_classes))
  coeff_mat[loss_matrix > 0] = 1
  coeff_mat[range(num_train), list(y)] = 0
  coeff_mat[range(num_train), list(y)] = -np.sum(coeff_mat, axis=1)

  dW = (X.T).dot(coeff_mat)
  dW /= num_train 
  dW += reg * W
  #############################################################################
  #                             END OF YOUR CODE                              #
  #############################################################################

  return loss, dW

这里面，有一句很难理解：

  loss_matrix = np.maximum(0, score - score[np.arange(num_train), np.array(y)].reshape(-1, 1) + 1)
当时看了很久，后来想通了，我们拆开来看，就不会很难了。

score[np.arange(num_train), np.array(y)]是从分数中，把正确的分数提取出来。下图中，那个小红框，就表示当前正确的分类对应的分数。提取出来之后，就是N*1维的矩阵

score - score[np.arange(num_train), np.array(y)].reshape(-1, 1)这个减法虽然维度不匹配，但是有boardcasting技术，后面的矩阵会自动列复制到维度N*C

 

 

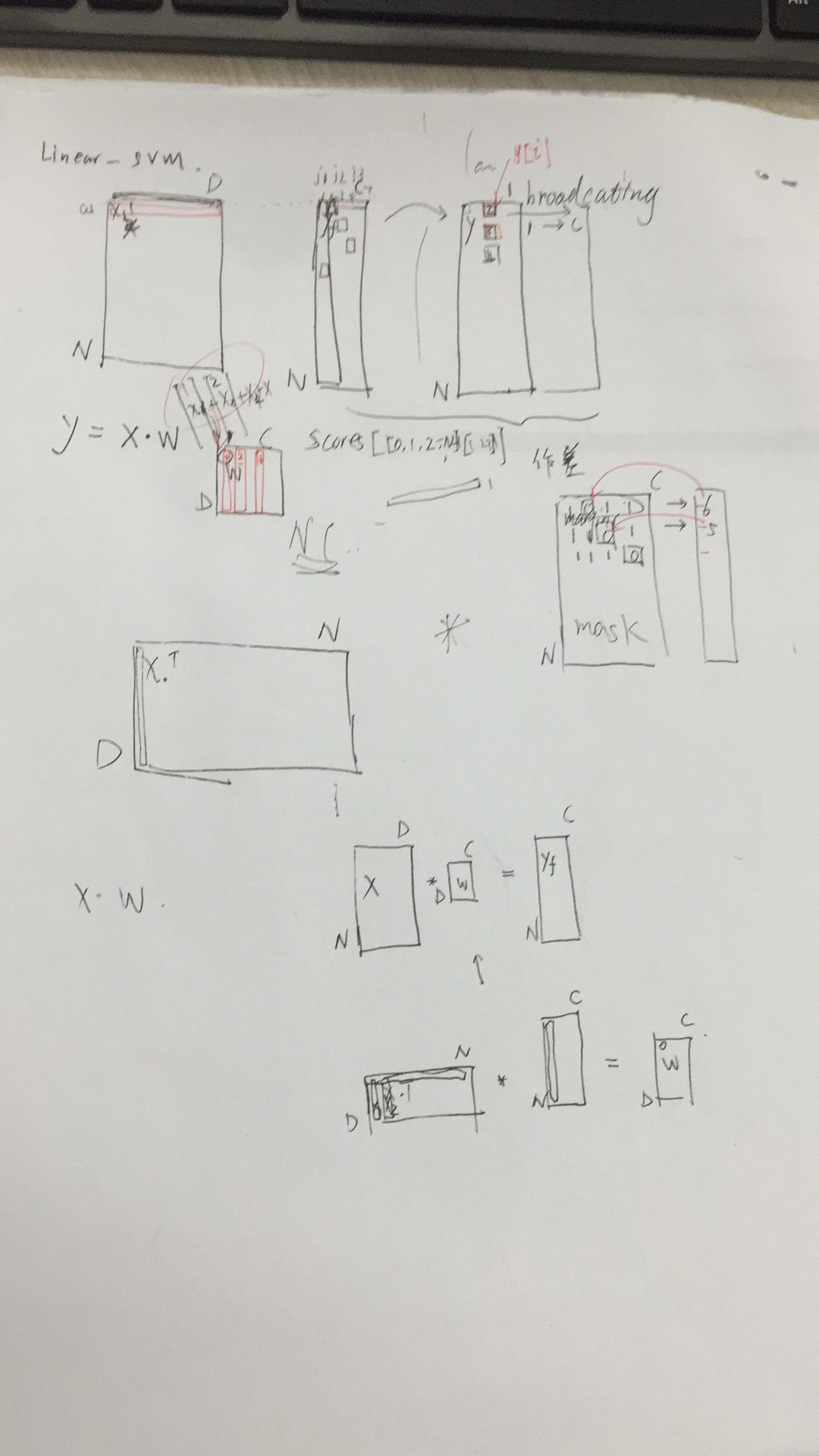
  num_classes = W.shape[1]
  coeff_mat = np.zeros((num_train, num_classes))
  coeff_mat[loss_matrix > 0] = 1
  coeff_mat[range(num_train), list(y)] = 0
  coeff_mat[range(num_train), list(y)] = -np.sum(coeff_mat, axis=1)

  dW = (X.T).dot(coeff_mat)
  dW /= num_train 
  dW += reg * W

 

  dW = (X.T).dot(coeff_mat) 这里dW 的计算，使用向量计算。用一个取值的coeff_mat矩阵来确定取哪些x加入。看懂循环是如何操作的，就明白了这个这里取巧的从X.T来实现循环，时间倍数16倍。

 

中间有几次，发现loss老是益处报错，后来才发现应该是learning rate 太大了，把-5改成-6，就可以了。原因是这里没有学习速率衰减优化策略