图
图简介:图是一种与树有些相像的数据结构,实际上,从数学意义上讲,树是图的一种。之前的数据结构都有一个框架,这个框架是由相应的算法规定的。例如,二叉树是那样一个形状,就是因为那样的形状使它容易搜索数据和插入新数据。树的边表示了从一个节点到另一个节点的快捷方式。另一方面,图通常有一个固定的形状,这是由物理或抽象的问题所决定的。
邻接:如果两个顶点被同一条边连接,就称这两个顶点是邻接的。
路径:路径是边的序列。例如从顶点B到顶点J,经过顶点A和顶点E,路径就为BAEJ。有可能路径不止一条。
连通图:如果至少有一条路径可以连接起所有的顶点,那么这个图被称作连通的。
有权图:在某些图中,边被赋予一个权值,权值是一个数字,它能代表两个顶点间的物理距离,或者从一个顶点到另一个顶点的时间,或者是两点间的花费,这样的图叫做带权图。
顶点:在大多数情况下,顶点表示某个真实世界的对象,这个对象必须用数据项来描述。示例:
public class Vertax {
private char label;
private boolean wasVisited;
Vertax(char label){
this.label = label;
this.wasVisited = false;
}
public char getLabel() {
return label;
}
public void setLabel(char label) {
this.label = label;
}
public boolean isWasVisited() {
return wasVisited;
}
public void setWasVisited(boolean wasVisited) {
this.wasVisited = wasVisited;
}
}
边:一般用两个方法表示图:邻接矩阵和邻接表。(如果一条边连接两个顶点,这两个顶点就是邻接的)。
邻接矩阵:是一个二维数组,数据项表示两点间是否存在边。如果图有N个顶点,邻接矩阵就是N*N的数组。
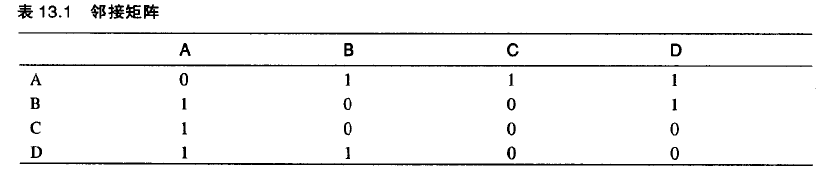
需要注意的是,矩阵的上三角是下三角的镜像:两个三角包含了相同的信息。这个冗余看似低效,但在大多数计算机语言中,创造一个三角形数组比较困难,所以只好求其次接受这个冗余。这也要求当增加一条边时,必须更新邻接矩阵的两部分,而不是一部分。
邻接表:是一种链表数组(或者是链表的链表)。
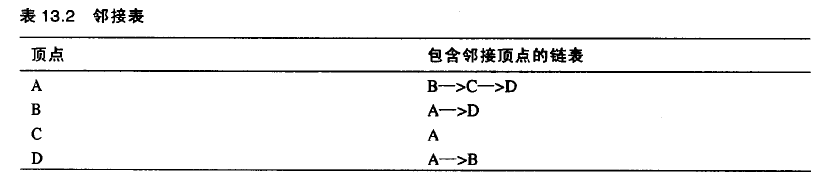
下面介绍图的遍历。有两种方式,深度优先遍历和广度优先遍历。深度优先搜索通过栈来实现,而广度优先搜索通过队列实现。
深度优先搜索:先找一个起始点,首先访问该顶点,然后把该点放入栈中,以便记住它,最后标记该点。
规则1:如果可能,访问一个邻接的未访问顶点,标记它,并把它放入栈中。
规则2:当不能执行规则1时,如果栈不空,就从栈中弹出一个顶点。
规则3:如果不能执行规则1和规则2,就完成了整个搜索过程。
深度优先搜索算法要得到距离起始点最远的顶点,然后在不能继续前进的时候返回。“深度”这个术语表示与起始点的距离。
模拟问题:深度优先搜索通常用在游戏仿真中(还有走迷宫问题)。在一般的游戏中,可以在几个可能的动作中选择一个,每个选择导致更进一步的选择,这些选择又产生了更多的选择,这样就形成了一个代表可能性的不断伸展的树形图。一个选择点代表一个顶点,采取的特定选择代表边,由它可以到达下一个选择顶点。
广度优先搜索:跟深度优先搜索相反,算法好像要尽可能地靠近起始点,它首先访问起始顶点的所有邻接点,然后再访问较远的区域。这种搜索不能用栈,而要用队列来实现。
规则1:访问下一个未来访问的邻接点(如果存在),这个顶点必须是当前顶点的邻接点,标记它,并把它插入到队列中。
规则2:如果因为已经没有未访问顶点而不能执行规则1,那么从队列头取一个顶点(如果存在),并使其成为当前节点。
规则2:如果因为队列为空而不能执行规则2,则搜索结束。
广度优先搜索有一个有趣的属性:它首先找到与起始点相距一条边的所有顶点,然后是与起始点相距两条边的顶点,依此类推。如果要寻找起始顶点到指定顶点的最短距离,那么这个属性非常有用。首先执行BFS,当找到指定顶点时,就可以说这条路径是到这个顶点的最短路径。
package graph;
import stack.Queue;
import stack.Stack;
//图
public class Graph {
private final static int MAX_LENGTH = 20;//顶点最大数,容量
private Vertax[] vertaxList;//顶点数组
private int[][] adjacentMatrix;//邻接矩阵
private int currentLength;//当前顶点数
Graph(){
vertaxList = new Vertax[MAX_LENGTH];
currentLength = 0;
adjacentMatrix = new int[MAX_LENGTH][MAX_LENGTH];
for(int i = 0;i < MAX_LENGTH;i++)
for(int j = 0;j < MAX_LENGTH;j++)
adjacentMatrix[i][j] = 0;
}
//添加顶点
public void addVertax(char ch){
vertaxList[currentLength++] = new Vertax(ch);
}
//添加节点后修改邻接矩阵
public void addEdge(int start,int end){
adjacentMatrix[start][end] = 1;
adjacentMatrix[end][start] = 1;
}
//展示顶点
public void displayVertax(int index){
System.out.println(vertaxList[index].getLabel());
}
//深度优先搜索
public void depthFirstSearch(){
vertaxList[0].setWasVisited(true);//标记成已访问状态
displayVertax(0);
Stack stack = new Stack();
stack.push(0);
int currentIndex;
while(!stack.isEmpty()){
currentIndex = (Integer)stack.peek();
currentIndex = getAdjacentVertax(currentIndex);
if(currentIndex != -1){
vertaxList[currentIndex].setWasVisited(true);
displayVertax(currentIndex);
stack.push(currentIndex);
}else{
stack.pop();
}
}
//重置成未访问状态
for(int i = 0;i < currentLength;i++){
vertaxList[i].setWasVisited(false);
}
}
//广度优先搜索
public void breadthFirstSearch(){
Queue queue = new Queue();
vertaxList[0].setWasVisited(true);//标记成已访问状态
displayVertax(0);
queue.insert(0);
int currentIndex;
while(!queue.isEmpty()){
currentIndex = (Integer)queue.peek();
currentIndex = getAdjacentVertax(currentIndex);
if(currentIndex == -1){
queue.remove();
}else{
vertaxList[currentIndex].setWasVisited(true);//标记成已访问状态
displayVertax(currentIndex);
queue.insert(currentIndex);
}
}
//重置成未访问状态
for(int i = 0;i < currentLength;i++){
vertaxList[i].setWasVisited(false);
}
}
//返回未访问过的邻接节点
public int getAdjacentVertax(int i){
for(int j = 0;j < currentLength;j++){
if(adjacentMatrix[i][j] == 1 && vertaxList[j].isWasVisited() == false){
return j;
}
}
return -1;
}
}
最小生成树:对于非带权图,最少的边连接所有的顶点,保证彼此连通,这就组成了最小生成树(MST)。注意,最小生成树边E的数量总比顶点V的数量小1:E = V - 1。记住,不必关心边的长度,并不需要找到一条最短路径,而是要找最少数量的边。(在带权图里面,这点会改变)。
创建最小生成树的算法与搜索的算法非常类似,在执行深度优先搜搜过程中,记录走过的边,就可以创建一棵最小生成树。这是因为DFS访问所有顶点,但只访问一次。
有向图:图有时需要一种前面没有涉及过的特性:边有方向。这时,图叫做有向图,在有向图中,只能沿着边指定的方向移动。在程序中,有向图与无向图的区别是有向图的边在邻接矩阵中只有一项。它的上下三角不是对称的。
拓扑排序:对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
规则1:找到一个没有后继节点的顶点。
规则2:从图中删除这个顶点,在列表的前面插入顶点的标记。



