Longest Substring Without Repeating Characters
今天的题目是：
Given a string, find the length of the longest substring without repeating characters.
Examples:
Given "abcabcbb", the answer is "abc", which the length is 3.
Given "bbbbb", the answer is "b", with the length of 1.
Given "pwwkew", the answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.
翻译一下：给一个字符串，找到无重复字符的最长子字符串的长度。
例如：字符串“abcabcbb”,答案是“abc”的长度为3。字符串“bbbbb”,答案是“b”的长度为1。字符串“pwwkew”,答案是“wke”的长度为3。要注意的是答案必须是子字符串，“pwke”是子序列并不是一个子字符串。
第一种解法：也是我能想到的最笨的方法，遍历。第一层从i = 0开始，第二层从 j = i + 1开始，每次判断从 i 到 j 的子字符串是否有重复字符，如果有，直接返回，如果没有，得出子字符串的长度，与之前的长度作比较取出最大值，作为最新的答案，循环结束后返回这个值。
package com.test;
import java.util.HashSet;
import java.util.Set;
public class Test {
@org.junit.Test
public void test(){
String s = "pwwkew";//未考虑空字符串
int length = 1;
for(int i = 0;i < s.length()-1;i++){
for(int j = i+1;j < s.length(); j++){
if(isNotRepeating(s,i,j))
length = Math.max(j-i+1, length);
}
}
System.out.println(s + "的最大子字符串长度为" + length);
}
public boolean isNotRepeating(String s,int start,int end){
Set<Character> set = new HashSet<Character>();
for(int i = start;i <= end;i++){
Character ch = s.charAt(i);
if(set.contains(ch)){
return false;
}else{
set.add(ch);
}
}
return true;
}
}
结果：
时间复杂度：O（N^3）。为了验证下标为i，j的字符集是否无重复，我们需要遍历它们，因此，这就花费了O（j-i）时间。对每一个i,花费时间为
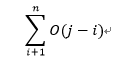，因此花费的时间总和是
。
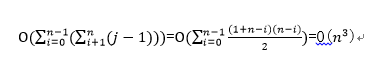空间复杂度：O（min(n,m)）。我们需要O（k）的空间大小来检查子字符串是否有重复字符，其中k的大小是Set的大小。k的上限是字符串的大小n或者是字符集的大小m（如果字符串所有的字符都是小写的英文字母，m就等于26）。
第二种解法：这种解法我也想过，但是我考虑的是用队列，这肯定耗时间。在第一种解法中，我们需要重复检查子字符串中是否有重复的字符。但是这并不是必须的。对于从i到j-1的子字符串已经检查了无重复的字符，我们下一步仅需要检查s[j]是否已经在从i到j-1的子字符串中。回到我们的问题，我们使用HashSet来存储字符集[i,j-1)，然后我们检查下标为j的字符是否已经在[i,j-1)中存在。如果未存在，我们就把s[j]加入到HashSet中，然后得到了当前无重复子字符串的最大长度，如果已存在，就把s[i]从HashSet中删除（从头开始删除，是不是像队列）。
package com.test;
import java.util.HashSet;
import java.util.Set;
public class Test {
@org.junit.Test
public void test(){
String s = "pwwkew";//未考虑空字符串
System.out.println(s + "的最大子字符串长度为" + getLongestSubStringLength(s));
}
public int getLongestSubStringLength(String s){
int length = 1,m = 0,n = 0;//非空字符串的不重复子字符串长度最小为1
int size = s.length();
HashSet<Character> set = new HashSet<Character>();
while(m < size && n < size){
if(!set.contains(s.charAt(m))){
set.add(s.charAt(m));
length = Math.max(length, m-n+1);
m++;
}else{
set.remove(s.charAt(n++));
}
}
return length;
}
}
结果：
时间复杂度：O（2n）= O（n）。
空间复杂度：O（min(n,m)），与第一种解法类似。
第三种解法：这种解法是对第二种解法的优化，事实上，它可以优化到只需要n步。我们不再使用set，而是使用map，将字符与其下标关联起来，这样当我们碰到重复字符时可以立刻定位到重复字符的下标。例如我们在[i,j)找到了与s[j]相同字符的下标k，这是我们不需要一步步加i，即i++，此时我们可以直接跳过，使i = k。
package com.test;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;
public class Test {
@org.junit.Test
public void test(){
String s = "pwwkew";//未考虑空字符串
System.out.println(s + "的最大子字符串长度为" + getLongestSubStringLength(s));
}
public int getLongestSubStringLength(String s){
int length = 1,n = 0;//非空字符串的不重复子字符串长度最小为1
int size = s.length();
Map<Character,Integer> map = new HashMap<Character,Integer>();
for(int m = 0;m < size;m++){
if(map.containsKey(s.charAt(m))){
n = Math.max(n, map.get(s.charAt(m)));
//map.remove(map.get(s.charAt(m)));//这个条件可以不加，加的话，下面的put相当于新添；不加的话下面的put是更新
}
length = Math.max(length, m-n);//计算下标为n到m的长度，但是不包括n，所以不用加1
map.put(s.charAt(m), m);
}
return length;
}
}
时间复杂度：O（n）。
空间复杂度：O（min(n,m)），与第一种解法类似。
第四种解法：以上的解法对字符串的字符集没有任何限制，事实上如果预先知道了字符集，并且字符集很小，可以考虑用数组的形式代替Map。
1，如果字符集是‘a’~'z'或者‘A’~‘Z’，可以考虑用int[26];
2，如果字符集是ASCII，则是int[128];
3，对于拓展的ASCII,则是int[256]。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
int[] index = new int[128]; // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
i = Math.max(index[s.charAt(j)], i);
ans = Math.max(ans, j - i + 1);
index[s.charAt(j)] = j + 1;
}
return ans;
}
}
此时的时间复杂度为O(n），空间复杂度为常量O(m),m为字符集的数量，例如上面的128。
