基于词典的前缀扫描中文分词

说明

中文分词是很多文本分析的基础。最近一个项目，输入一个地址，需要识别出地址中包含的省市区街道等单词。与以往的分词技术不同。jieba/hanlp等常用的分词技术，除了基于词典，还有基于隐马尔科夫/条件随机场等机器学习技术对未登录词的分词，有一定的概率性。而我们所使用的地址识别，要求必须基于词库进行精确的分词。这些比较高级的分词技术反而成为了不必要的风险。

另外还有一个原因是，流行的分词技术对多用户词典和词典的动态管理支持也不是很好。本项目就实现了一个可以多词典间相互隔离的分词工具。

基于前缀词典树的中文分词概念简单。其中使用到的trie树/有向无环图（dag）/动态规划计算最长路径等算法，可以说是教科书一样的例子。所以我就自己实现了一遍，测试下来效果还不错。

Trie树（前缀词典树）

trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。 

 

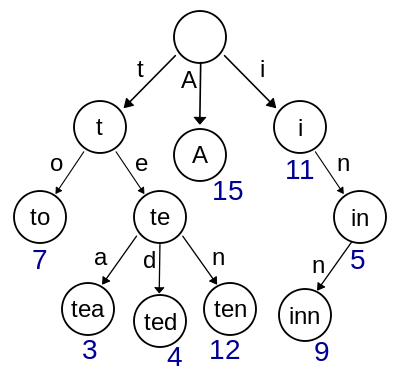
在图示中，键标注在节点中，值标注在节点之下。每一个完整的单词对应一个特定的整数。

键不需要被显式地保存在节点中。图示中标注出完整的单词，只是为了演示trie的原理。 

trie中的键通常是字符串，但也可以是其它的结构。trie的算法可以很容易地修改为处理其它结构的有序序列，比如一串数字或者形状的排列。比如，bitwise trie中的键是一串位元，可以用于表示整数或者内存地址。

在本实现中，节点的值主要是单词的词频。

初始化时，往根节点中添加一个单词，以及对应的词频。根节点生成子节点递归调用。但是这里方法并没有写成递归，而是写成了循环。因为，递归相对来说不好理解，而且debug也不显而易见。一个基本原则是，对于java这种非函数式语言，凡是使用递归的地方都可以改成循环。

    public void fillSegment(char[] charArray, int wordFrequency) {
        int count = charArray.length;
        CharNode charNode = this;
        for (int i = 0; i < count; i++) {
            CharNode child = charNode.searchOrAddChild(charArray[i]);
            charNode = child;
        }
        charNode.wordFrequency += wordFrequency;
    }

初始化后，就是搜索了。传入一个字符串，指定从哪个字符开始搜索，找到所有可能匹配的单词。这里就体现出了trie树优于hashmap的地方。在trie树中，一旦找不到子节点，就可以返回了。但hash并不具有这种特性，hash需要把字符串的所有子字符串遍历一遍才知道。

    public List<HitWord> match(char[] chars, int beginIndex) {
        List<HitWord> result = new ArrayList<>();
        int count = chars.length;
        if (beginIndex >= count - 1) {
            return result;
        }
        CharNode charNode = this;
        for (int i = beginIndex; i < count; i++) {
            CharNode tmpCharNode = charNode.searchChild(chars[i]);
            if (tmpCharNode == null) {
                break;
            }
            charNode = tmpCharNode;
            if (tmpCharNode.wordFrequency > 0) {
                HitWord hitWord = new HitWord(i, tmpCharNode.wordFrequency);
                result.add(hitWord);
            }
        }
        return result;
    }

这里返回结果是一个list，因为一个字符串可能匹配到多个结果。比如“上海市”去匹配，词库里有“上海”和“上海市”，那返回的就是List.size() == 2的结果。

DAG（有向无环图）

一个语句根据词频生成一个有向无环图。分词的原理我懒得说了。看下这个链接吧。http://www.cnblogs.com/zhbzz2007/p/6084196.html。

生成dag的关键代码如下。

    private List<List<HitWord>> createDag(String sentence){
        List<List<HitWord>> result = new ArrayList<>();
        char[] chars = sentence.toCharArray();
        int count = chars.length;
        for(int i = 0; i < count; i++){
            List<HitWord> matchList = dictionaryMgr.match(chars, i, this.dictionaryKey);
            result.add(matchList);
        }
        return result;
    }

生成的结果是一个二维List。第一维下标对应句子字符串下标。第二维下标对应图的路径：路径包含路径终点下标及路径权重（词频）。

下面是基于dag寻找最优路径。这里用到了动态规划的思想。由于每个节点都是有下标的，而且路径的起点下标恒大于终点下标，基于这个特点，其实这个动态规划实现的还是比较简单粗暴的。不过还好，还算非常简单有效。

    private Map<Integer, Integer> calculateRouter(List<List<HitWord>> dag){
        int count = dag.size();
        Map<Integer, Integer> router = new HashMap<>(count);
        double[] frequencies = new double[count + 1];
        for(int i = count - 1; i >= 0; i--){
            List<HitWord> list = dag.get(i);
            if(list.isEmpty()){
                frequencies[i] = frequencies[i + 1];
                continue;
            }
            for (HitWord hitWord : list) {
                int endIndex = hitWord.getEndIndex();
                double tmpFrequency = hitWord.getFrequency() + frequencies[endIndex + 1];
                if(tmpFrequency > frequencies[i]){
                    frequencies[i] = tmpFrequency;
                    router.put(i, endIndex);
                }
            }
        }
        return router;
    }

分词

有了路径，就可以分词了。路径是一个map，key为起点，value为终点。根据路径进行分词，就很简单了。

    private List<String> cutFromRouter(String sentence, Map<Integer, Integer> router){
        List<String> result = new ArrayList<>();
        int count = sentence.length();
        for(int i = 0; i < count; i++){
            int j = i;
            if(router.containsKey(i)){
                j = router.get(i);
            }
            String word = sentence.substring(i, j + 1);
            i = j;
            result.add(word);
        }
        return  result;
    }

最后是分词入口，将生成dag，生成router，分词的 三个方法连起来。

    public List<String> cut(String sentence){
        List<List<HitWord>> dag = this.createDag(sentence);
        Map<Integer, Integer> router = this.calculateRouter(dag);
        return this.cutFromRouter(sentence, router);
    }

附：

代码git，https://github.com/shlugood/wordcut 如果感兴趣，可下载下来。pom项目，还带有测试词典和UT。

看下我跑的UT吧。

[北京, 顺义区, 李桥镇, 馨, 港, 庄, 园, 8, 区, 8, 0, 号, 楼, 1, 2, 3, 单, 元, 2, 0, 1]
[浙江, 杭州市, 余杭区, 五常街道, 西, 溪, 庭, 院, 9, 8, —, 2, —, 4, 4, 4]
[广东, 深圳市, 宝安区, 松岗街道, 松岗镇, 溪, 头, 村, 委, 西, 六, 十, 七, 巷, 一, 百, 二, 十, 三, 号]