使用PARL与Gym仿真环境进行深度Q学习(DQL)
blog翻译。原blog:https://keon.github.io/deep-q-learning/
强化学习
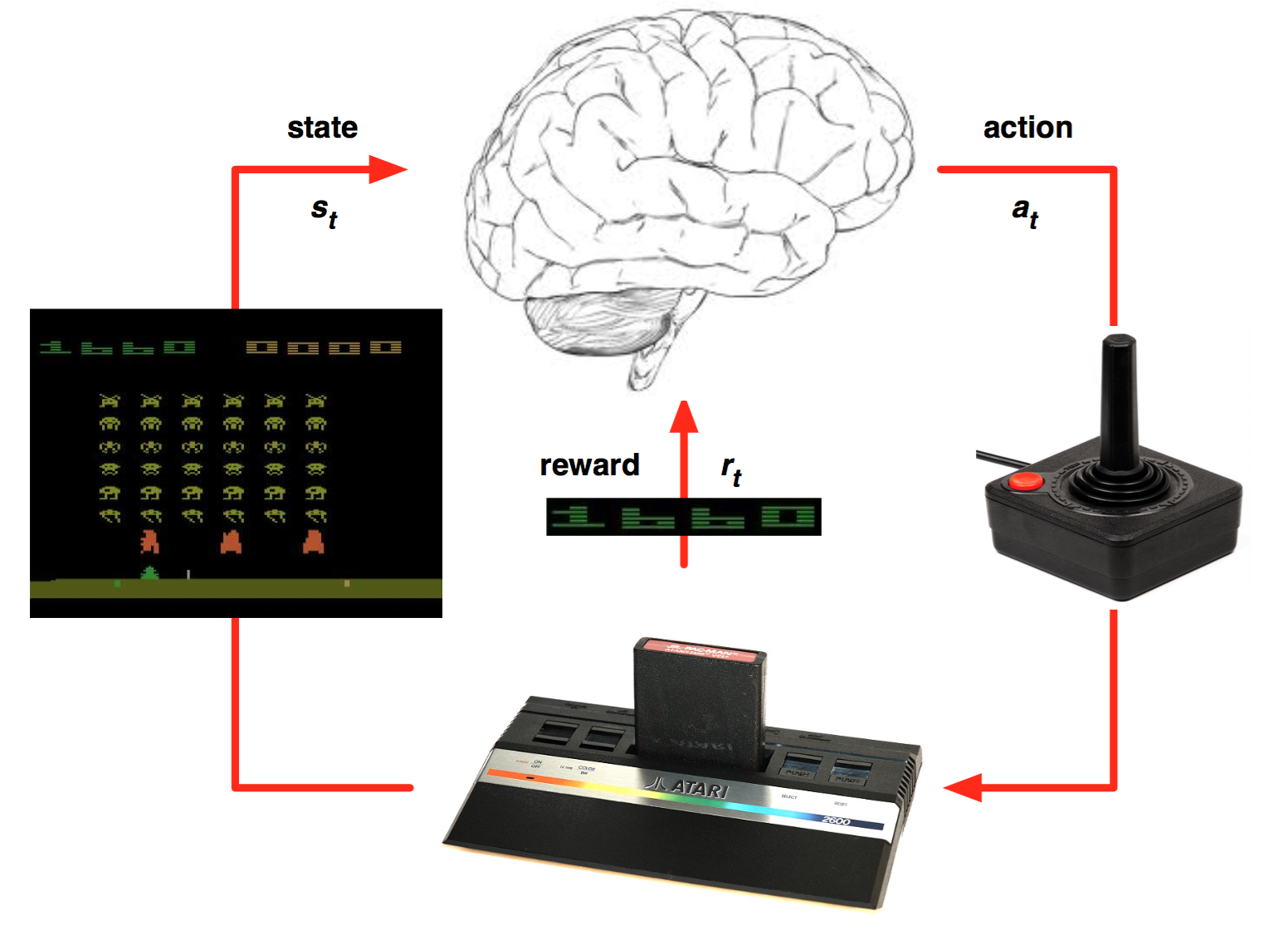
强化学习是一种允许你创造能从环境中交互学习的AI agent 的机器学习算法。就跟我们学习骑自行车一样,这种类型的AI通过试错来学习。如上图所示,大脑代表AI agent并在环境中活动。当每次行动过后,agent接收到环境反馈。反馈包括回报(reward)和环境的下个状态(state)。回报由模型设计者定义。如果类比人类学习自行车,我们会将车从起始点到当前位置的距离定义为回报。
深度强化学习
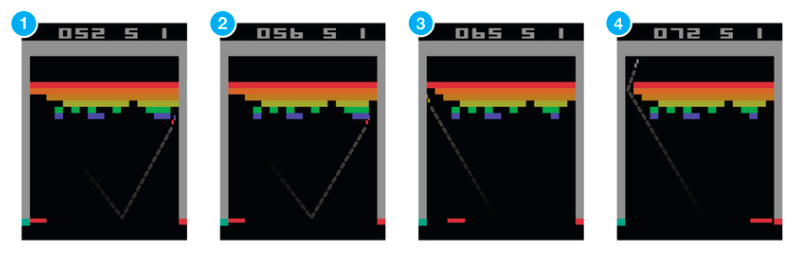
2013年,在DeepMind 发表的著名论文Playing Atari with Deep Reinforcement Learning中,他们介绍了一种新算法,深度Q网络(DQN)。文章展示了AI agent如何在没有任何先验信息的情况下通过观察屏幕学习玩游戏。结果令人印象深刻。这篇文章开启了被我们成为“深度强化学习”的新时代。这种学习算法是混合了深度学习与强化学习的新算法。
在Q学习算法中,有一种函数被称为Q函数,它用来估计基于一个状态的回报。同样地,在DQN中,我们使用一个神经网络估计基于状态的回报函数。我们将在之后细致地讨论这一部分工作。
Cartpole游戏
通常训练一个agent玩Atari游戏通常会好一会儿(从几个小时到一天)。所以我们将训练agent玩一个简单的游戏,CartPole,并使用在上面论文中的一些思想。
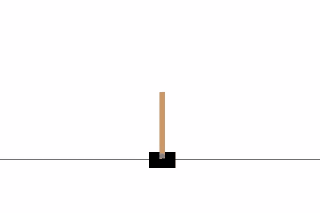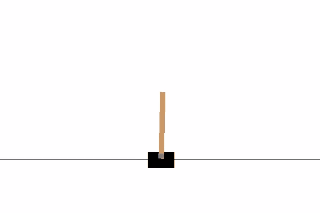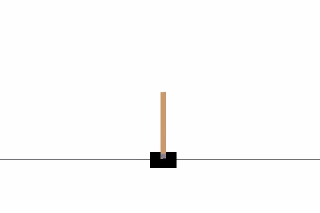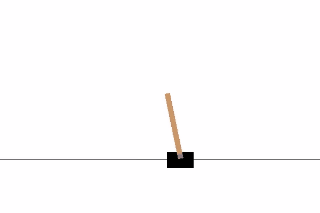
CartPole是OpenAI gym中最简单的一个环境。正如你在文章一开始看到的那个gif一样,CartPole的目的就是杆子平衡在移动的小车上。除了像素信息,还有四种信息可以用作状态,像是,杆子的角度和车在滑轨的位置。agent可以通过施加左(0)或右(1)的动作,使小车移动。
Gym使游戏环境的交互非常方便:
next_state, reward, done, info = env.step(action)
如我们上面所说,action要么是0要么是1。当我们将这些数字串入环境中将会得出结果。“env”是游戏环境类。“done”为标记游戏结束与否的布尔量。当前状态“state”,“action”,“next_state”与“reward”是我们用于训练agent的数据。
使用PaddlePaddle实现简单神经网络
这篇文章不是关于深度学习或神经网络的。所以我们将神经网络试做黑箱算法。这个算法的功能是从成对的输入与输出数据学习某种模式并且可以基于不可见的输入数据预测输出。但是我们应该理解在DQN算法中的那部分神经网络算法。
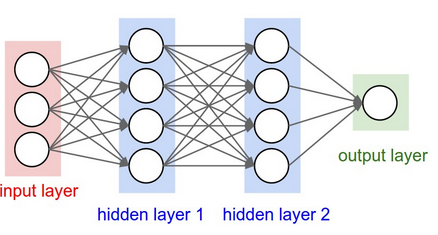
注意到我们使用的神经网络类似于上图所示的网络。我们使用一个包含四种输入信息的输入层和三个隐藏层。但是我们在输出层有两个节点因为在这个游戏中有两个按钮(0与1)。
下面的代码会生成一个拥有两个全连接层的神经网络模型。
import parl
from parl import layers
import paddle.fluid as fluid
import copy
import numpy as np
import os
import gym
from parl.utils import logger
class Model(parl.Model):
def __init__(self, act_dim):
hid1_size = 128
hid2_size = 128
# 3层全连接网络
self.fc1 = layers.fc(size=hid1_size, act='relu')
self.fc2 = layers.fc(size=hid2_size, act='relu')
self.fc3 = layers.fc(size=act_dim, act=None)
def value(self, obs):
# 定义网络
# 输入state,输出所有action对应的Q,[Q(s,a1), Q(s,a2), Q(s,a3)...]
h1 = self.fc1(obs)
h2 = self.fc2(h1)
Q = self.fc3(h2)
return Q
实现深度Q算法(DQN)
DQN算法最重要的特征是记忆(remember)与回顾(replay)方法。它们都有很简明的概念。
记忆(remember)
对于DQN来说一个挑战就是运用在算法中的神经网络区域通过覆盖掉先前学习的经验来遗忘它们。所以我们需要记录下先前的经验与观察值以便再用这些先前数据训练模型。我们将调用代表经验的数组数据“memory”和“remember()”函数来添加状态,回报,和下次状态到“memory”中。
在本例中,“memory”列表中有以下形式的数据:
memory = [(state, action, reward, next_State)...]
具体的实现在下方给出:
import random
import collections
import numpy as np
class ReplayMemory(object):
def __init__(self, max_size):
self.buffer = collections.deque(maxlen=max_size)
# 增加一条经验到经验池中
def append(self, exp):
self.buffer.append(exp)
# 从经验池中选取N条经验出来
def sample(self, batch_size):
mini_batch = random.sample(self.buffer, batch_size)
obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], []
for experience in mini_batch:
s, a, r, s_p, done = experience
obs_batch.append(s)
action_batch.append(a)
reward_batch.append(r)
next_obs_batch.append(s_p)
done_batch.append(done)
return np.array(obs_batch).astype('float32'), \
np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'),\
np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32')
def __len__(self):
return len(self.buffer)
回放(replay)
“回放“的意思就是从存储在“memory”中的数据(经验)中训练神经网络。我们在每次训练网络时会抽出一些数据,这些数据被称作batches,在下列的训练函数中,rpm.sample(BATCH_SIZE)方法就是从buffer中随机抽出一部分数据然后训练agent中的网络。
# 训练一个episode
def run_episode(env, agent, rpm):
total_reward = 0
obs = env.reset()
step = 0
while True:
step += 1
action = agent.sample(obs) # 采样动作,所有动作都有概率被尝试到
next_obs, reward, done, _ = env.step(action)
rpm.append((obs, action, reward, next_obs, done))
# train model
if (len(rpm) > MEMORY_WARMUP_SIZE) and (step % LEARN_FREQ == 0):
(batch_obs, batch_action, batch_reward, batch_next_obs,
batch_done) = rpm.sample(BATCH_SIZE)
train_loss = agent.learn(batch_obs, batch_action, batch_reward,
batch_next_obs,
batch_done) # s,a,r,s',done
total_reward += reward
obs = next_obs
if done:
break
return total_reward
# 评估 agent, 跑 5 个episode,总reward求平均
def evaluate(env, agent, render=False):
eval_reward = []
for i in range(5):
obs = env.reset()
episode_reward = 0
while True:
action = agent.predict(obs) # 预测动作,只选最优动作
obs, reward, done, _ = env.step(action)
episode_reward += reward
if render:
env.render()
if done:
break
eval_reward.append(episode_reward)
return np.mean(eval_reward)
为了使agent在长期运行中表现的更好,我们不仅仅需要考虑即时回报(immediate rewards),还要考虑未来回报(future rewards)。为了实现这一目标,我们定义“discount rate”(折扣因子) 即“gamma”。这样,agent将学习已有的状态然后想方设法最大化未来回报。
class DQN(parl.Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" DQN algorithm
Args:
model (parl.Model): 定义Q函数的前向网络结构
act_dim (int): action空间的维度,即有几个action
gamma (float): reward的衰减因子
lr (float): learning rate 学习率.
"""
self.model = model
self.target_model = copy.deepcopy(model)
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
assert isinstance(lr, float)
self.act_dim = act_dim
self.gamma = gamma
self.lr = lr
def predict(self, obs):
""" 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...]
"""
return self.model.value(obs)
def learn(self, obs, action, reward, next_obs, terminal):
""" 使用DQN算法更新self.model的value网络
"""
# 从target_model中获取 max Q' 的值,用于计算target_Q
next_pred_value = self.target_model.value(next_obs)
best_v = layers.reduce_max(next_pred_value, dim=1)
best_v.stop_gradient = True # 阻止梯度传递
terminal = layers.cast(terminal, dtype='float32')
target = reward + (1.0 - terminal) * self.gamma * best_v
pred_value = self.model.value(obs) # 获取Q预测值
# 将action转onehot向量,比如:3 => [0,0,0,1,0]
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
# 下面一行是逐元素相乘,拿到action对应的 Q(s,a)
# 比如:pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
# ==> pred_action_value = [[3.9]]
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
# 计算 Q(s,a) 与 target_Q的均方差,得到loss
cost = layers.square_error_cost(pred_action_value, target)
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(learning_rate=self.lr) # 使用Adam优化器
optimizer.minimize(cost)
return cost
def sync_target(self):
""" 把 self.model 的模型参数值同步到 self.target_model
"""
self.model.sync_weights_to(self.target_model)
agent如何选择行为?
我们的agent在最初的一部分时间会随机选择行为,这被“exploration rate”或“epsilon”参数表征。这是因为在最初对agent最好的策略就是在他们掌握模式前尝试一切。当agent没有随机选择行为,它会基于当前状态预测回报值并且选择能够将回报最大化的行为。“np.argmax()”函数可以取出“act_values[0]”中的最大值。
class Agent(parl.Agent):
def __init__(self,
algorithm,
obs_dim,
act_dim,
e_greed=0.1,
e_greed_decrement=0):
assert isinstance(obs_dim, int)
assert isinstance(act_dim, int)
self.obs_dim = obs_dim
self.act_dim = act_dim
super(Agent, self).__init__(algorithm)
self.global_step = 0
self.update_target_steps = 200 # 每隔200个training steps再把model的参数复制到target_model中
self.e_greed = e_greed # 有一定概率随机选取动作,探索
self.e_greed_decrement = e_greed_decrement # 随着训练逐步收敛,探索的程度慢慢降低
def build_program(self):
self.pred_program = fluid.Program()
self.learn_program = fluid.Program()
with fluid.program_guard(self.pred_program): # 搭建计算图用于 预测动作,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
self.value = self.alg.predict(obs)
with fluid.program_guard(self.learn_program): # 搭建计算图用于 更新Q网络,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
action = layers.data(name='act', shape=[1], dtype='int32')
reward = layers.data(name='reward', shape=[], dtype='float32')
next_obs = layers.data(
name='next_obs', shape=[self.obs_dim], dtype='float32')
terminal = layers.data(name='terminal', shape=[], dtype='bool')
self.cost = self.alg.learn(obs, action, reward, next_obs, terminal)
def sample(self, obs):
sample = np.random.rand() # 产生0~1之间的小数
if sample < self.e_greed:
act = np.random.randint(self.act_dim) # 探索:每个动作都有概率被选择
else:
act = self.predict(obs) # 选择最优动作
self.e_greed = max(
0.01, self.e_greed - self.e_greed_decrement) # 随着训练逐步收敛,探索的程度慢慢降低
return act
def predict(self, obs): # 选择最优动作
obs = np.expand_dims(obs, axis=0)
pred_Q = self.fluid_executor.run(
self.pred_program,
feed={'obs': obs.astype('float32')},
fetch_list=[self.value])[0]
pred_Q = np.squeeze(pred_Q, axis=0)
act = np.argmax(pred_Q) # 选择Q最大的下标,即对应的动作
return act
def learn(self, obs, act, reward, next_obs, terminal):
# 每隔200个training steps同步一次model和target_model的参数
if self.global_step % self.update_target_steps == 0:
self.alg.sync_target()
self.global_step += 1
act = np.expand_dims(act, -1)
feed = {
'obs': obs.astype('float32'),
'act': act.astype('int32'),
'reward': reward,
'next_obs': next_obs.astype('float32'),
'terminal': terminal
}
cost = self.fluid_executor.run(
self.learn_program, feed=feed, fetch_list=[self.cost])[0] # 训练一次网络
return cost
超参数
有一些超参数是强化学习agent所必需的,你会在下面一次又一次的看到这些参数。
episodes 我们想让agent玩游戏的次数
gamma discount rate(折扣因子),以便计算未来的折扣回报。
epsilon exploration rate,这个比率表征一个agent随机选择行为的程度
epsilon_decay 上述参数的衰减率。我们希望随着agent更擅长游戏的同时减少它探索的次数。
learning_rata 这个参数决定了神经网络在每次迭代时的学习率(学习程度)。
LEARN_FREQ = 5 # 训练频率,不需要每一个step都learn,攒一些新增经验后再learn,提高效率
MEMORY_SIZE = 20000 # replay memory的大小,越大越占用内存
MEMORY_WARMUP_SIZE = 200 # replay_memory 里需要预存一些经验数据,再开启训练
BATCH_SIZE = 32 # 每次给agent learn的数据数量,从replay memory随机里sample一批数据出来
LEARNING_RATE = 0.001 # 学习率
GAMMA = 0.99 # reward 的衰减因子,一般取 0.9 到 0.999 不等
EPISODES = 2000
让我们来训练它吧!
env = gym.make('CartPole-v0') # CartPole-v0: 预期最后一次评估总分 > 180(最大值是200)
action_dim = env.action_space.n # CartPole-v0: 2
obs_shape = env.observation_space.shape # CartPole-v0: (4,)
rpm = ReplayMemory(MEMORY_SIZE) # DQN的经验回放池
# 根据parl框架构建agent
model = Model(act_dim=action_dim)
algorithm = DQN(model, act_dim=action_dim, gamma=GAMMA, lr=LEARNING_RATE)
agent = Agent(
algorithm,
obs_dim=obs_shape[0],
act_dim=action_dim,
e_greed=0.1, # 有一定概率随机选取动作,探索
e_greed_decrement=1e-6) # 随着训练逐步收敛,探索的程度慢慢降低
# 加载模型
# save_path = './dqn_model.ckpt'
# agent.restore(save_path)
# 先往经验池里存一些数据,避免最开始训练的时候样本丰富度不够
while len(rpm) < MEMORY_WARMUP_SIZE:
run_episode(env, agent, rpm)
# 开始训练
episode = 0
while episode < EPISODES: # 训练max_episode个回合,test部分不计算入episode数量
# train part
for i in range(0, 50):
total_reward = run_episode(env, agent, rpm)
episode += 1
# test part
eval_reward = evaluate(env, agent, render=False) # render=True 查看显示效果
logger.info('episode:{} e_greed:{} test_reward:{}'.format(
episode, agent.e_greed, eval_reward))
[32m[06-25 23:06:44 MainThread @machine_info.py:88][0m Cannot find available GPU devices, using CPU now.
[32m[06-25 23:06:44 MainThread @machine_info.py:88][0m Cannot find available GPU devices, using CPU now.
[32m[06-25 23:06:45 MainThread @machine_info.py:88][0m Cannot find available GPU devices, using CPU now.
[32m[06-25 23:06:48 MainThread @<ipython-input-15-b87386821719>:36][0m episode:50 e_greed:0.098997999999999 test_reward:10.4
[32m[06-25 23:06:50 MainThread @<ipython-input-15-b87386821719>:36][0m episode:100 e_greed:0.0984899999999985 test_reward:9.0
[32m[06-25 23:06:52 MainThread @<ipython-input-15-b87386821719>:36][0m episode:150 e_greed:0.097989999999998 test_reward:10.0
[32m[06-25 23:06:53 MainThread @<ipython-input-15-b87386821719>:36][0m episode:200 e_greed:0.09748699999999749 test_reward:9.6
[32m[06-25 23:06:55 MainThread @<ipython-input-15-b87386821719>:36][0m episode:250 e_greed:0.09698199999999699 test_reward:9.2
[32m[06-25 23:06:57 MainThread @<ipython-input-15-b87386821719>:36][0m episode:300 e_greed:0.09648699999999649 test_reward:9.6
[32m[06-25 23:06:59 MainThread @<ipython-input-15-b87386821719>:36][0m episode:350 e_greed:0.09598399999999599 test_reward:9.8
[32m[06-25 23:07:01 MainThread @<ipython-input-15-b87386821719>:36][0m episode:400 e_greed:0.09542399999999543 test_reward:10.4
[32m[06-25 23:07:03 MainThread @<ipython-input-15-b87386821719>:36][0m episode:450 e_greed:0.0947999999999948 test_reward:9.0
[32m[06-25 23:07:07 MainThread @<ipython-input-15-b87386821719>:36][0m episode:500 e_greed:0.09396599999999397 test_reward:12.2
[32m[06-25 23:07:24 MainThread @<ipython-input-15-b87386821719>:36][0m episode:550 e_greed:0.0901009999999901 test_reward:176.4
[32m[06-25 23:08:07 MainThread @<ipython-input-15-b87386821719>:36][0m episode:600 e_greed:0.08040699999998041 test_reward:194.0
[32m[06-25 23:08:47 MainThread @<ipython-input-15-b87386821719>:36][0m episode:650 e_greed:0.07106699999997107 test_reward:193.4
[32m[06-25 23:09:24 MainThread @<ipython-input-15-b87386821719>:36][0m episode:700 e_greed:0.062443999999962446 test_reward:145.0
[32m[06-25 23:10:03 MainThread @<ipython-input-15-b87386821719>:36][0m episode:750 e_greed:0.05348999999995349 test_reward:200.0
[32m[06-25 23:10:37 MainThread @<ipython-input-15-b87386821719>:36][0m episode:800 e_greed:0.045924999999945926 test_reward:178.4
[32m[06-25 23:11:10 MainThread @<ipython-input-15-b87386821719>:36][0m episode:850 e_greed:0.03836299999993836 test_reward:121.8
[32m[06-25 23:11:47 MainThread @<ipython-input-15-b87386821719>:36][0m episode:900 e_greed:0.030014999999930014 test_reward:125.8
[32m[06-25 23:12:20 MainThread @<ipython-input-15-b87386821719>:36][0m episode:950 e_greed:0.022796999999922796 test_reward:146.4
[32m[06-25 23:12:51 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1000 e_greed:0.015602999999915641 test_reward:144.4
[32m[06-25 23:13:26 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1050 e_greed:0.01 test_reward:122.2
[32m[06-25 23:13:49 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1100 e_greed:0.01 test_reward:118.4
[32m[06-25 23:14:19 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1150 e_greed:0.01 test_reward:200.0
[32m[06-25 23:14:49 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1200 e_greed:0.01 test_reward:111.8
[32m[06-25 23:15:18 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1250 e_greed:0.01 test_reward:179.8
[32m[06-25 23:15:49 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1300 e_greed:0.01 test_reward:122.2
[32m[06-25 23:16:20 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1350 e_greed:0.01 test_reward:149.2
[32m[06-25 23:16:49 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1400 e_greed:0.01 test_reward:135.8
[32m[06-25 23:17:21 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1450 e_greed:0.01 test_reward:200.0
[32m[06-25 23:17:59 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1500 e_greed:0.01 test_reward:162.8
[32m[06-25 23:18:31 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1550 e_greed:0.01 test_reward:107.6
[32m[06-25 23:19:14 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1600 e_greed:0.01 test_reward:200.0
[32m[06-25 23:19:58 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1650 e_greed:0.01 test_reward:200.0
[32m[06-25 23:20:37 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1700 e_greed:0.01 test_reward:200.0
[32m[06-25 23:21:22 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1750 e_greed:0.01 test_reward:200.0
[32m[06-25 23:22:06 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1800 e_greed:0.01 test_reward:200.0
[32m[06-25 23:22:51 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1850 e_greed:0.01 test_reward:200.0
[32m[06-25 23:23:36 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1900 e_greed:0.01 test_reward:200.0
[32m[06-25 23:24:06 MainThread @<ipython-input-15-b87386821719>:36][0m episode:1950 e_greed:0.01 test_reward:200.0
[32m[06-25 23:24:50 MainThread @<ipython-input-15-b87386821719>:36][0m episode:2000 e_greed:0.01 test_reward:200.0
经过几百个episodes的训练后,它开始学习如何最大化分数。当500episode之后,它的test_reward达到了最大。在1500episode后,一个大师级CartPole玩家终于诞生啦。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号