20182323 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结
目录
学号20182323 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结
教材学习内容总结
第19章
图的基本概念
-
线性表和树两类数据结构,线性表中的元素是“一对一”的关系,树中的元素是“一对多”的关系,本章所述的图结构中的元素则是“多对多”的关系。
图是一种复杂的非线性结构,在图结构中,每个元素都可以有零个或多个前驱,也可以有零个或多个后继,也就是说,元素之间的关系是任意的。
-
无向图:无向图是由顶点和边构成。
-
有向图:有向图是由顶点和有向边构成。
-
完全图:如果任意两个顶点之间都存在边叫完全图,有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图。
图的节点访问
/**
* 无向简单图的节点
* @author caoqian
*/
public class GraphNode<T> {
T data;
List<GraphNode<T>> neighborList;
boolean visited;
public GraphNode(T data){
this.data = data;
neighborList = new ArrayList<GraphNode<T>>();
visited = false;
}
public boolean equals(GraphNode<T> node){
return this.data.equals(node.data);
}
/**
* 还原图中所有节点为未访问
*/
public void restoreVisited(){
restoreVisited(this);
}
/**
* 还原node的图所有节点为未访问
* @param node
*/
private void restoreVisited(GraphNode<T> node){
if(node.visited){
node.visited = false;
}
List<GraphNode<T>> neighbors = node.neighborList;
for(int i = 0; i < neighbors.size(); i++){
restoreVisited(neighbors.get(i));
}
}
}
图的深度优先和广度优先搜索
1.深度优先
1.1、介绍:
图的深度优先搜索,和树的先序遍历比较类似。
思路:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。显然,深度优先搜索是一个递归的过程。
1.2、无向图深度优先搜索图解
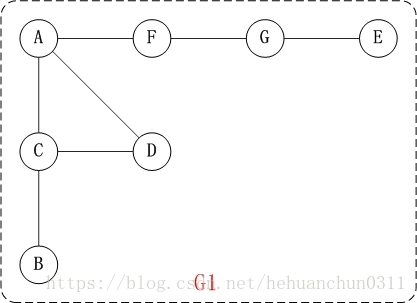
对上面的图G1进行深度优先遍历,从顶点A开始。

第1步:访问A。
第2步:访问(A的邻接点)C。在第1步访问A之后,接下来应该访问的是A的邻接点,即”C,D,F”中的一个。但在本文的实现中,顶点ABCDEFG是按照顺序存储,C在”D和F”的前面,因此,先访问C。
第3步:访问(C的邻接点)B。在第2步访问C之后,接下来应该访问C的邻接点,即”B和D”中一个(A已经被访问过,就不算在内)。而由于B在D之前,先访问B。
第4步:访问(C的邻接点)D。
第5步:访问(A的邻接点)F。
第6步:访问(F的邻接点)G。
第7步:访问(G的邻接点)E。
访问顺序是:A -> C -> B -> D -> F -> G -> E
1.3、无向图深度优先搜索图解
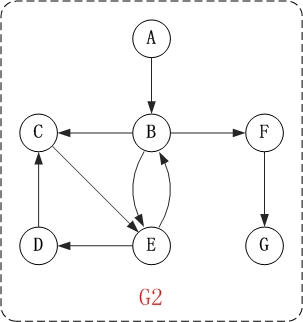
对上面的图G2进行深度优先遍历,从顶点A开始。
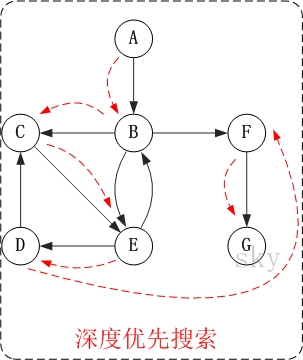
访问顺序是:A -> B -> C -> E -> D -> F -> G
2.广度优先
2.1、介绍
从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远。
2.2、无向图广度优先搜索图解

访问顺序是:A -> C -> D -> F -> B -> G -> E
2.3、有向图广度优先搜索图解
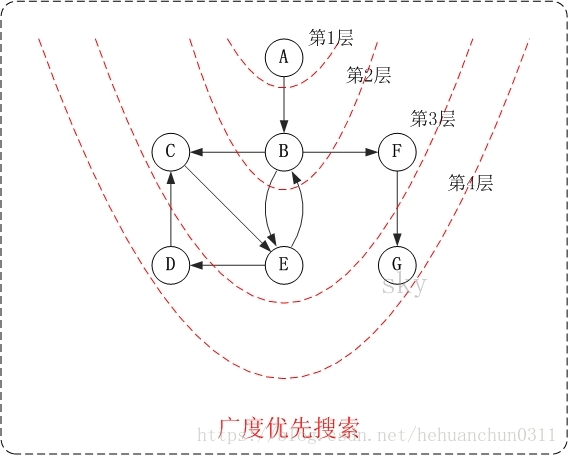
访问顺序是:A -> B -> C -> E -> F -> D -> G
图的邻接表和邻接矩阵
图的存储结构主要分两种,一种是邻接矩阵,一种是邻接表。
1.邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
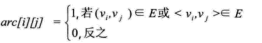
看一个实例,下图左就是一个无向图。

从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
(1)要判断任意两顶点是否有边无边就很容易了;
(2)要知道某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
(3)求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点;
而有向图讲究入度和出度,顶点vi的入度为1,正好是第i列各数之和。顶点vi的出度为2,即第i行的各数之和。
若图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
2.邻接表
邻接矩阵是不错的一种图存储结构,但是,对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。因此,找到一种数组与链表相结合的存储方法称为邻接表。
邻接表的处理方法是这样的:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
例如,下图就是一个无向图的邻接表的结构。
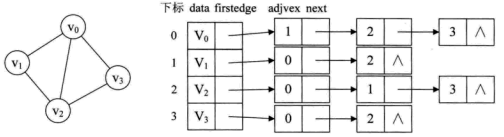
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。如下图所示。

教材学习中的问题和解决过程
-
问题1:图的广度优先搜索和深度优先搜索实现
-
问题1解决方案:
public class GraphSearch<T> {
public StringBuffer searchPathDFS = new StringBuffer();
public StringBuffer searchPathBFS = new StringBuffer();
/**
* 深度优先搜索实现
*
*/
public void searchDFS(GraphNode<T> root) {
if (root == null) {
return;
}
// visited root
if (searchPathDFS.length() > 0) {
searchPathDFS.append("->");
}
searchPathDFS.append(root.data.toString());
root.visited = true;
for (GraphNode<T> node : root.neighborList) {
if (!node.visited) {
searchDFS(node);
}
}
}
/**
* 广度优先搜索实现,使用队列
*
*/
public void searchBFS(GraphNode<T> root) {
IQueue<GraphNode<T>> queue = new Queue<GraphNode<T>>();
// visited root
if (searchPathBFS.length() > 0) {
searchPathBFS.append("->");
}
searchPathBFS.append(root.data.toString());
root.visited = true;
// 加到队列队尾
queue.enqueue(root);
while (!queue.isEmpty()) {
GraphNode<T> r = queue.dequeue();
for (GraphNode<T> node : r.neighborList) {
if (!node.visited) {
searchPathBFS.append("->");
searchPathBFS.append(node.data.toString());
node.visited = true;
queue.enqueue(node);
}
}
}
}
}
代码调试中的问题和解决过程
-
问题1:代码出现问题

-
解决过程:后来在对之前写过的代码进行排查发现,是LinkedList类没有声明StackADT这个接口。
上周错题
上周无错题
代码托管

结对及互评
点评模板:
-
博客中值得学习的或问题:
- 随着学习内容难度增加,问题分析更加深刻
- 不断查阅资料,努力解决出现的问题
-
代码中值得学习的或问题:
- 代码的逻辑性有待提高
- 代码中适当加入注释会更好
-
基于评分标准,我给本博客打分:12分。得分情况如下:
-
正确使用Markdown语法(加1分):
- 不使用Markdown不加分
- 有语法错误的不加分(链接打不开,表格不对,列表不正确...)
- 排版混乱的不加分
-
模板中的要素齐全(加1分)
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程(2分)
-
代码调试中的问题和解决过程(2分)
-
本周有效代码超过300分行的(加0分)
-
其他加分:
- 周五前发博客的加1分
- 感想,体会不假大空的加1分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
点评过的同学博客和代码
- 本周结对学习情况
- 结对同学学号20182315
- 结对照片
- 结对学习内容
- 图的概念,图的节点访问,图的深度优先和广度优先搜索,图的邻接表和邻接矩阵
其他(感悟、思考等,可选)
继续潜心学习,只问初心,无问西东。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 77/77 | 2/2 | 15/15 | |
| 第三周 | 424/501 | 3/5 | 30/30 | |
| 第四周 | 393/894 | 2/7 | 30/30 | |
| 第五周 | 320/1214 | 1/8 | 30/30 | |
| 第六周 | 904/2118 | 2/10 | 30/30 | |
| 第7周 | 1350/3468 | 3/13 | 30/30 | |
| 第8周 | 342/3810 | 1/14 | 30/30 | |
| 第9周 | 6048/9858 | 4/18 | 30/30 | |
| 第10周 | 1063/10921 | 2/20 | 30/30 |
-
计划学习时间:25小时
-
实际学习时间:20小时
-
改进情况:



