哈夫曼树讲解
哈夫曼树讲解
一、哈夫曼树的概念和定义
这里举一个例子来引出判定树:
在很多问题的处理过程中,需要进行大量的条件判断,这些判断结构的设计直接影响着程序的执行效率。例如,编制一个程序,将百分制转换成五个等级输出。大家可能认为这个程序很简单,并且很快就可以用下列形式编写出来:
if(score<60)
cout<<"Bad"<<endl;
else if(score<70)
cout<<"Pass"<<endl
else if(score<80)
cout<<"General"<<endl;
else if(score<90)
cout<<"Good"<<endl;
else
cout<<"Very good!"<<endl;
若考虑上述程序所耗费的时间,就会发现该程序的缺陷。在实际中,学生成绩在五个等级上的分布是不均匀的。当学生百分制成绩的录入量很大时,上述判定过程需要反复调用,此时程序的执行效率将成为一个严重问题。
但在实际应用中,往往各个分数段的分布并不是均匀的。
下面我们就利用哈夫曼树寻找一棵最佳判定树,即总的比较次数最少的判定树。
第一种构造方式:
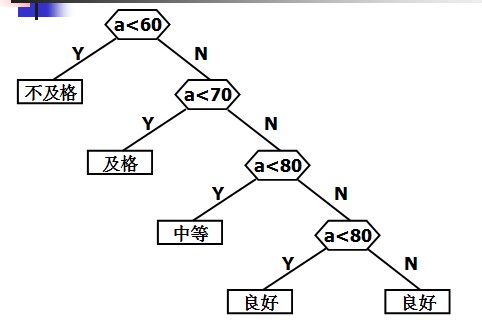
第二种构造方式:
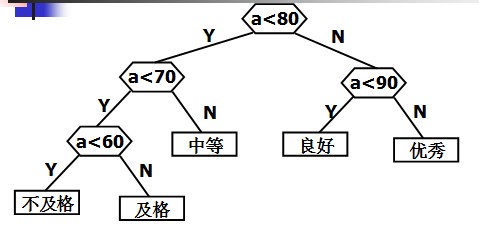
这两种方式,显然后者的判定过程的效率要比前者高。在也没有别地判定过程比第二种方式的效率更高。
我们称判定过程最优的二叉树为哈夫曼树,又称最优二叉树
========================================
定义哈夫曼树之前先说明几个与哈夫曼树有关的概念:
路径: 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度:路径上的分枝数目称作路径长度。
树的路径长度:从树根到每一个结点的路径长度之和。
结点的带权路径长度:在一棵树中,如果其结点上附带有一个权值,通常把该结点的路径长度与该结点上的权值之积称为该结点的带权路径长度。
树的带权路径长度:如果树中每个叶子上都带有一个权值,则把树中所有叶子的带权路径长度之和称为树的带权路径长度。
带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树
二、哈夫曼树的构造
++注意:哈夫曼树并不唯一,但带权路径长度一定是相同的。++
由给定结点构造哈夫曼树:
(1) 8个结点的权值大小如下:

(2). 从19,21,2,3,6,7,10,32中选择两个权小结点。选中2,3。同时算出这两个结点的和5。

(3). 从19,21,6,7,10,32,5中选出两个权小结点。选中
5,6。同时计算出它们的和11。

(4). 从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。(PS:这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。)
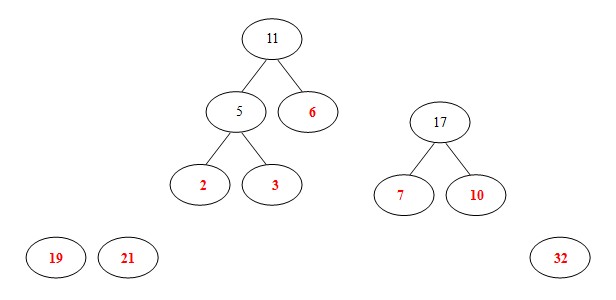
(5). 从19,21,32,11,17中选出两个权小结点。选中11,17。同时计算出它们的和28。
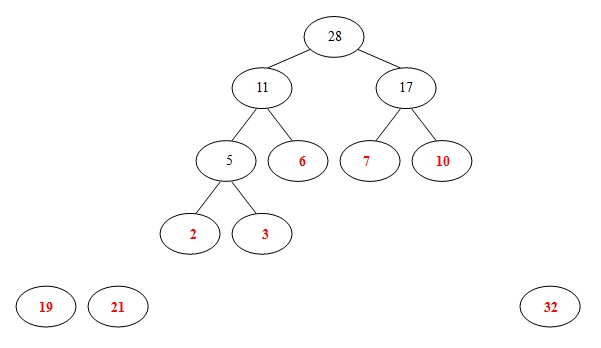
(6). 从19,21,32,28中选出两个权小结点。选中19,21。同时计算出它们的和40。另起一颗二叉树。
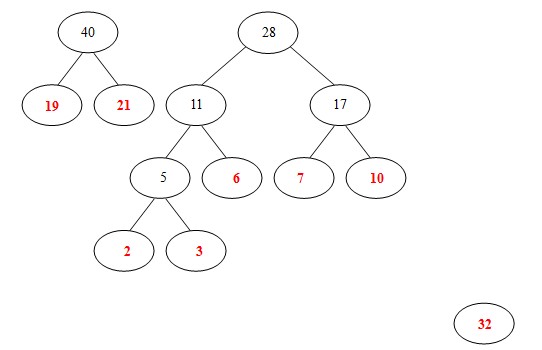
(7). 从32,28, 40中选出两个权小结点。选中28,32。同时计算出它们的和60。
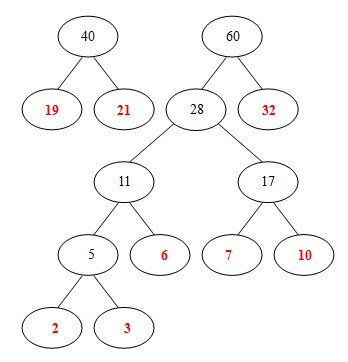
(8). 从 40, 60中选出两个权小结点。选中40,60。同时计算出它们的和100。 好了,此时哈夫曼树已经构建好了。
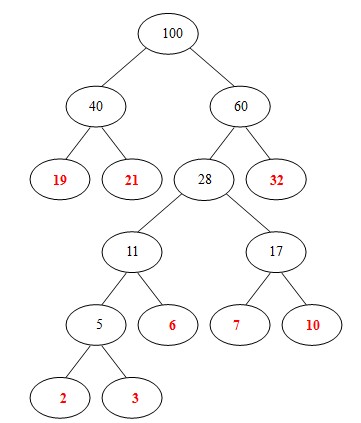
课堂测试

错因:自以为弄明白了哈夫曼树的构造原理,结果并没有将每次计算和之后的序列进行排序选择。
正解:根据上诉方法,我已画出了正确的图(图有点丑,这里就不粘上来啦),正确的带权路径长度为2.71.




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 因为Apifox不支持离线,我果断选择了Apipost!
· 通过 API 将Deepseek响应流式内容输出到前端