深度学习：数值稳定性、房价预测、模型构造
1、数值稳定性和模型初始化
深度模型有关数值稳定性的典型问题是衰减（vanishing）和爆炸（explosion）。
1.1衰减和爆炸
当神经网络的层数较多时，模型的数值稳定性容易变差。假设一个层数为\(L\)的多层感知机的第\(l\)层\(\boldsymbol{H}^{(l)}\)的权重参数为\(\boldsymbol{W}^{(l)}\)，输出层\(\boldsymbol{H}^{(L)}\)的权重参数为\(\boldsymbol{W}^{(L)}\)。为了便于讨论，不考虑偏差参数，且设所有隐藏层的激活函数为恒等映射（identity mapping）\(\phi(x) = x\)。给定输入\(\boldsymbol{X}\)，多层感知机的第\(l\)层的输出\(\boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)}\)。此时，如果层数\(l\)较大，\(\boldsymbol{H}^{(l)}\)的计算可能会出现衰减或爆炸。举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知机的第30层输出为输入\(\boldsymbol{X}\)分别与\(0.2^{30} \approx 1 \times 10^{-21}\)（衰减）和\(5^{30} \approx 9 \times 10^{20}\)（爆炸）的乘积。类似地，当层数较多时，梯度的计算也更容易出现衰减或爆炸。
1.2随机初始化模型参数
在神经网络中，通常需要随机初始化模型参数。
原因：
如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有1个隐藏单元在发挥作用。因此，正如在前面的实验中所做的那样，我们通常对神经网络的模型参数，特别是权重参数，进行随机初始化。
- MXNet的默认随机初始化
MXNet将使用默认的随机初始化方法：权重参数每个元素随机采样于-0.07到0.07之间的均匀分布，偏差参数全部清零。
- Xavier随机初始化
假设某全连接层的输入个数为\(a\)，输出个数为\(b\)，Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
它的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层输出个数影响。
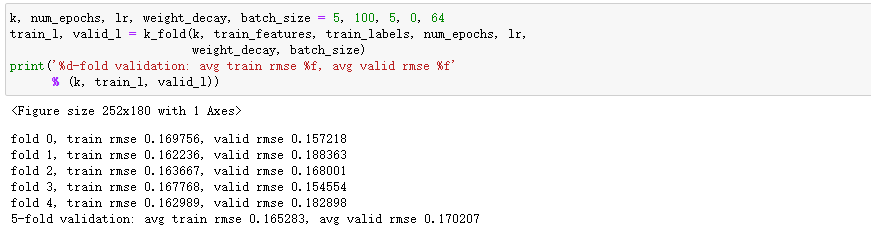
2、房价预测
查看前4个样本的前4个特征、后2个特征和标签（SalePrice）：
对连续数值的特征做标准化（standardization）：设该特征在整个数据集上的均值为 𝜇 ，标准差为 𝜎 。那么，我们可以将该特征的每个值先减去 𝜇 再除以 𝜎 得到标准化后的每个特征值。对于缺失的特征值，我们将其替换成该特征的均值。
将离散数值转成指示特征。
通过values属性得到NumPy格式的数据，并转成NDArray方便后面的训练。
我们使用一个基本的线性回归模型和平方损失函数来训练模型
3、模型构造
介绍另外一种基于Block类的模型构造方法：它让模型构造更加灵活。
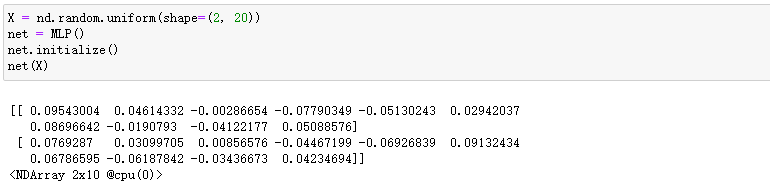
继承Block类来构造模型
Block类是nn模块里提供的一个模型构造类，我们可以继承它来定义我们想要的模型。下面继承Block类构造本节开头提到的多层感知机。这里定义的MLP类重载了Block类的__init__函数和forward函数。它们分别用于创建模型参数和定义前向计算。前向计算也即正向传播。
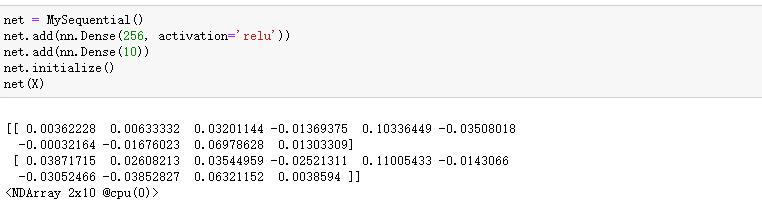
Sequential类继承自Block类
我们刚刚提到，Block类是一个通用的部件。事实上，Sequential类继承自Block类。当模型的前向计算为简单串联各个层的计算时，可以通过更加简单的方式定义模型。这正是Sequential类的目的：它提供add函数来逐一添加串联的Block子类实例，而模型的前向计算就是将这些实例按添加的顺序逐一计算。
构造复杂的模型
虽然Sequential类可以使模型构造更加简单，且不需要定义forward函数，但直接继承Block类可以极大地拓展模型构造的灵活性。下面我们构造一个稍微复杂点的网络FancyMLP。在这个网络中，我们通过get_constant函数创建训练中不被迭代的参数，即常数参数。在前向计算中，除了使用创建的常数参数外，我们还使用NDArray的函数和Python的控制流，并多次调用相同的层。
4、参考文献
《深度学习》
