深度学习：权重衰减、丢弃法、反向传播

1、权重衰减

过拟合现象：模型的训练误差远小于它在测试集上的误差。

虽然增大训练数据集可能会减轻过拟合，但是获取额外的训练数据往往代价高昂。

本节介绍应对过拟合问题的常用方法：权重衰减（weight decay）。

方法

权重衰减等价于$L_2$范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。我们先描述$L_2$范数正则化，再解释它为何又称权重衰减。

$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项，从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以“线性回归”一节中的线性回归损失函数

$$\ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2$$

为例，其中$w_1, w_2$是权重参数，$b$是偏差参数，样本$i$的输入为$x_1^{(i)}, x_2^{(i)}$，标签为$y^{(i)}$，样本数为$n$。将权重参数用向量$\boldsymbol{w} = [w_1, w_2]$表示，带有$L_2$范数惩罚项的新损失函数为

$$\ell(w_1, w_2, b) + \frac{\lambda}{2} \|\boldsymbol{w}\|^2,$$

其中超参数$\lambda > 0$。当权重参数均为0时，惩罚项最小。当$\lambda$较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时，惩罚项完全不起作用。上式中$L_2$范数平方$\|\boldsymbol{w}\|^2$展开后得到$w_1^2 + w_2^2$。有了$L_2$范数惩罚项后，在小批量随机梯度下降中，我们将“线性回归”一节中权重$w_1$和$w_2$的迭代方式更改为

$$\begin{aligned} w_1 &\leftarrow \left(1- \eta\lambda \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow \left(1- \eta\lambda \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned}$$

可见，$L_2$范数正则化令权重$w_1$和$w_2$先自乘小于1的数，再减去不含惩罚项的梯度。因此，$L_2$范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。实际场景中，我们有时也在惩罚项中添加偏差元素的平方和。

简洁实现

点击查看代码

def fit_and_plot_gluon(wd):
    net = nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize(init.Normal(sigma=1))
    # 对权重参数衰减。权重名称一般是以weight结尾
    trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd',
                              {'learning_rate': lr, 'wd': wd})
    # 不对偏差参数衰减。偏差名称一般是以bias结尾
    trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd',
                              {'learning_rate': lr})
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                l = loss(net(X), y)
            l.backward()
            # 对两个Trainer实例分别调用step函数，从而分别更新权重和偏差
            trainer_w.step(batch_size)
            trainer_b.step(batch_size)
        train_ls.append(loss(net(train_features),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),
                            test_labels).mean().asscalar())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net[0].weight.data().norm().asscalar())

2、丢弃法

除了权重衰减以外，深度学习模型常常使用丢弃法（dropout）来应对过拟合问题。

方法

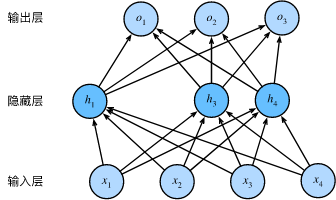
一个单隐藏层的多层感知机:其中输入个数为4，隐藏单元个数为5，且隐藏单元$h_i$（$i=1, \ldots, 5$）的计算表达式为

$$h_i = \phi\left(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_i\right),$$

这里$\phi$是激活函数，$x_1, \ldots, x_4$是输入，隐藏单元$i$的权重参数为$w_{1i}, \ldots, w_{4i}$，偏差参数为$b_i$。当对该隐藏层使用丢弃法时，该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为$p$，
那么有$p$的概率$h_i$会被清零，有$1-p$的概率$h_i$会除以$1-p$做拉伸。丢弃概率是丢弃法的超参数。具体来说，设随机变量$\xi_i$为0和1的概率分别为$p$和$1-p$。使用丢弃法时我们计算新的隐藏单元$h_i'$

$$h_i' = \frac{\xi_i}{1-p} h_i.$$

由于$E(\xi_i) = 1-p$，因此

$$E(h_i') = \frac{E(\xi_i)}{1-p}h_i = h_i.$$

即丢弃法不改变其输入的期望值。

对隐藏层使用丢弃法，一种可能的结果如图3.5所示，其中$h_2$和$h_5$被清零。这时输出值的计算不再依赖$h_2$和$h_5$，在反向传播时，与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的，即$h_1, \ldots, h_5$都有可能被清零，输出层的计算无法过度依赖$h_1, \ldots, h_5$中的任一个，从而在训练模型时起到正则化的作用，并可以用来应对过拟合。在测试模型时，我们为了得到更加确定性的结果，一般不使用丢弃法。

简洁实现

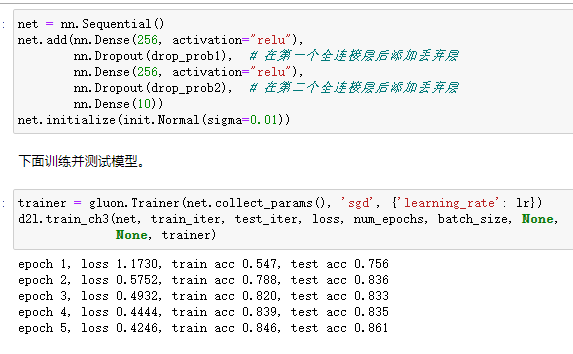
在Gluon中，我们只需要在全连接层后添加Dropout层并指定丢弃概率。在训练模型时，Dropout层将以指定的丢弃概率随机丢弃上一层的输出元素；在测试模型时，Dropout层并不发挥作用。

• 我们可以通过使用丢弃法应对过拟合。
• 丢弃法只在训练模型时使用。

3、正向传播、反向传播和计算图

前面几节里我们使用了小批量随机梯度下降的优化算法来训练模型。在实现中，我们只提供了模型的正向传播的计算，即对输入计算模型输出，然后通过autograd模块来调用系统自动生成的backward函数计算梯度。基于反向传播算法的自动求梯度极大简化了深度学习模型训练算法的实现。本节我们将使用数学来描述正向传播和反向传播。具体来说，我们将以带$L_2$范数正则化的含单隐藏层的多层感知机为样例模型解释正向传播和反向传播。

正向传播

正向传播（forward propagation）是指对神经网络沿着从输入层到输出层的顺序，依次计算并存储模型的中间变量（包括输出）。为简单起见，假设输入是一个特征为$\boldsymbol{x} \in \mathbb{R}^d$的样本，且不考虑偏差项，那么中间变量

$$\boldsymbol{z} = \boldsymbol{W}^{(1)} \boldsymbol{x},$$

其中$\boldsymbol{W}^{(1)} \in \mathbb{R}^{h \times d}$是隐藏层的权重参数。把中间变量$\boldsymbol{z} \in \mathbb{R}^h$输入按元素运算的激活函数$\phi$后，将得到向量长度为$h$的隐藏层变量

$$\boldsymbol{h} = \phi (\boldsymbol{z}).$$

隐藏层变量$\boldsymbol{h}$也是一个中间变量。假设输出层参数只有权重$\boldsymbol{W}^{(2)} \in \mathbb{R}^{q \times h}$，可以得到向量长度为$q$的输出层变量

$$\boldsymbol{o} = \boldsymbol{W}^{(2)} \boldsymbol{h}.$$

假设损失函数为$\ell$，且样本标签为$y$，可以计算出单个数据样本的损失项

$$L = \ell(\boldsymbol{o}, y).$$

根据$L_2$范数正则化的定义，给定超参数$\lambda$，正则化项即

$$s = \frac{\lambda}{2} \left(\|\boldsymbol{W}^{(1)}\|_F^2 + \|\boldsymbol{W}^{(2)}\|_F^2\right),$$

其中矩阵的Frobenius范数等价于将矩阵变平为向量后计算$L_2$范数。最终，模型在给定的数据样本上带正则化的损失为

$$J = L + s.$$

我们将$J$称为有关给定数据样本的目标函数，并在以下的讨论中简称目标函数。

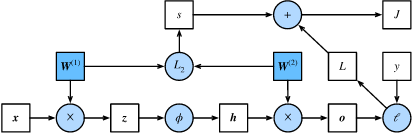
正向传播的计算图

我们通常绘制计算图（computational graph）来可视化运算符和变量在计算中的依赖关系。图3.6绘制了本节中样例模型正向传播的计算图，其中左下角是输入，右上角是输出。可以看到，图中箭头方向大多是向右和向上，其中方框代表变量，圆圈代表运算符，箭头表示从输入到输出之间的依赖关系。

反向传播

反向传播（back-propagation）指的是计算神经网络参数梯度的方法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输入层的顺序，依次计算并存储目标函数有关神经网络各层的中间变量以及参数的梯度。对输入或输出$\mathsf{X}, \mathsf{Y}, \mathsf{Z}$为任意形状张量的函数$\mathsf{Y}=f(\mathsf{X})$和$\mathsf{Z}=g(\mathsf{Y})$，通过链式法则，我们有

$$\frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \text{prod}\left(\frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}, \frac{\partial \mathsf{Y}}{\partial \mathsf{X}}\right),$$

其中$\text{prod}$运算符将根据两个输入的形状，在必要的操作（如转置和互换输入位置）后对两个输入做乘法。

回顾一下本节中样例模型，它的参数是$\boldsymbol{W}^{(1)}$和$\boldsymbol{W}^{(2)}$，因此反向传播的目标是计算$\partial J/\partial \boldsymbol{W}^{(1)}$和$\partial J/\partial \boldsymbol{W}^{(2)}$。我们将应用链式法则依次计算各中间变量和参数的梯度，其计算次序与前向传播中相应中间变量的计算次序恰恰相反。首先，分别计算目标函数$J=L+s$有关损失项$L$和正则项$s$的梯度

$$\frac{\partial J}{\partial L} = 1, \quad \frac{\partial J}{\partial s} = 1.$$

其次，依据链式法则计算目标函数有关输出层变量的梯度$\partial J/\partial \boldsymbol{o} \in \mathbb{R}^q$：

$$\frac{\partial J}{\partial \boldsymbol{o}} = \text{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial \boldsymbol{o}}\right) = \frac{\partial L}{\partial \boldsymbol{o}}.$$

接下来，计算正则项有关两个参数的梯度：

$$\frac{\partial s}{\partial \boldsymbol{W}^{(1)}} = \lambda \boldsymbol{W}^{(1)},\quad\frac{\partial s}{\partial \boldsymbol{W}^{(2)}} = \lambda \boldsymbol{W}^{(2)}.$$

现在，我们可以计算最靠近输出层的模型参数的梯度$\partial J/\partial \boldsymbol{W}^{(2)} \in \mathbb{R}^{q \times h}$。依据链式法则，得到

$$\frac{\partial J}{\partial \boldsymbol{W}^{(2)}} = \text{prod}\left(\frac{\partial J}{\partial \boldsymbol{o}}, \frac{\partial \boldsymbol{o}}{\partial \boldsymbol{W}^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \boldsymbol{W}^{(2)}}\right) = \frac{\partial J}{\partial \boldsymbol{o}} \boldsymbol{h}^\top + \lambda \boldsymbol{W}^{(2)}.$$

沿着输出层向隐藏层继续反向传播，隐藏层变量的梯度$\partial J/\partial \boldsymbol{h} \in \mathbb{R}^h$可以这样计算：

$$\frac{\partial J}{\partial \boldsymbol{h}} = \text{prod}\left(\frac{\partial J}{\partial \boldsymbol{o}}, \frac{\partial \boldsymbol{o}}{\partial \boldsymbol{h}}\right) = {\boldsymbol{W}^{(2)}}^\top \frac{\partial J}{\partial \boldsymbol{o}}.$$

由于激活函数$\phi$是按元素运算的，中间变量$\boldsymbol{z}$的梯度$\partial J/\partial \boldsymbol{z} \in \mathbb{R}^h$的计算需要使用按元素乘法符$\odot$：

$$\frac{\partial J}{\partial \boldsymbol{z}} = \text{prod}\left(\frac{\partial J}{\partial \boldsymbol{h}}, \frac{\partial \boldsymbol{h}}{\partial \boldsymbol{z}}\right) = \frac{\partial J}{\partial \boldsymbol{h}} \odot \phi'\left(\boldsymbol{z}\right).$$

最终，我们可以得到最靠近输入层的模型参数的梯度$\partial J/\partial \boldsymbol{W}^{(1)} \in \mathbb{R}^{h \times d}$。依据链式法则，得到

$$\frac{\partial J}{\partial \boldsymbol{W}^{(1)}} = \text{prod}\left(\frac{\partial J}{\partial \boldsymbol{z}}, \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{W}^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \boldsymbol{W}^{(1)}}\right) = \frac{\partial J}{\partial \boldsymbol{z}} \boldsymbol{x}^\top + \lambda \boldsymbol{W}^{(1)}.$$

• 正向传播沿着从输入层到输出层的顺序，依次计算并存储神经网络的中间变量。
• 反向传播沿着从输出层到输入层的顺序，依次计算并存储神经网络的中间变量和参数的梯度。
• 在训练深度学习模型时，正向传播和反向传播相互依赖。

参考文献

《动手学深度学习》