机器学习:聚类
1、聚类任务
聚类是一种经典的无监督学习方法,无监督学习的目标是通过对无标记训练样本的学习,发掘和揭示数据集本身潜在的结构与规律,即不依赖于训练数据集的类标记信息。
聚类则是试图将数据集的样本划分为若干个互不相交的类簇,从而每个簇对应一个潜在的类别。
2、性能度量
性能度量为评价聚类结果的好坏提供了一系列有效性指标。
一般聚类有两类性能度量指标:外部指标和内部指标。
2.1外部指标
-
即将聚类结果与某个参考模型的结果进行比较,以参考模型的输出作为标准,来评价聚类好坏。假设聚类给出的结果为λ,参考模型给出的结果是λ*
-

-
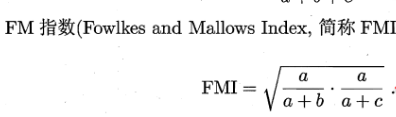
-

2.2内部指标
内部指标即不依赖任何外部模型,直接对聚类的结果进行评估,聚类的目的是想将那些相似的样本尽可能聚在一起,不相似的样本尽可能分开。

3、距离计算
- 最常用的距离度量方法是“闵可夫斯基距离”(Minkowski distance):
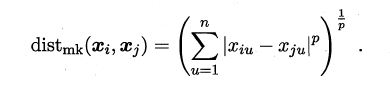
- 当p=2时,闵可夫斯基距离即欧氏距离(Euclidean distance):
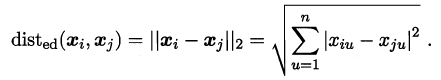
- 当p=1时,闵可夫斯基距离即曼哈顿距离(Manhattan distance):
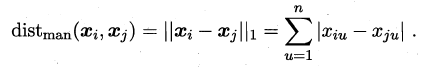
属性分为两种:连续属性和离散属性(有限个取值)。
- 连续值的属性,一般都可以被学习器所用,有时会根据具体的情形作相应的预处理,例如:归一化等;
- 离散值的属性,需要作下面进一步的处理:
- 若属性值之间存在序关系,则可以将其转化为连续值,例如:身高属性“高”“中等”“矮”,可转化为{1, 0.5, 0}。
- 闵可夫斯基距离
- 若属性值之间不存在序关系,则通常将其转化为向量的形式,例如:性别属性“男”“女”,可转化为{(1,0),(0,1)}。
- VDM(Value Difference Metric)
- 若属性值之间存在序关系,则可以将其转化为连续值,例如:身高属性“高”“中等”“矮”,可转化为{1, 0.5, 0}。
4、聚类方法
4.1原型聚类
原型聚类即“基于原型的聚类”(prototype-based clustering),原型表示模板的意思,就是通过参考一个模板向量或模板分布的方式来完成聚类的过程,常见的K-Means便是基于簇中心来实现聚类,混合高斯聚类则是基于簇分布来实现聚类。
Kmeans

学习向量量化(LVQ)
与k均值算法类似, “学习向量量化” (Learning Vector Quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
首先LVQ根据样本的类标记,从各类中分别随机选出一个样本作为该类簇的原型,从而组成了一个原型特征向量组,接着从样本集中随机挑选一个样本,计算其与原型向量组中每个向量的距离,并选取距离最小的原型向量所在的类簇作为它的划分结果,再与真实类标比较。

4.2密度聚类
密度聚类则是基于密度的聚类(density-based clustering),它从样本分布的角度来考察样本之间的可连接性,并基于可连接性(密度可达)不断拓展疆域(类簇)。其中最著名的便是DBSCAN算法。
主要思想:找出一个核心对象所有密度可达的样本集合形成簇。首先从数据集中任选一个核心对象A,找出所有A密度可达的样本集合,将这些样本形成一个密度相连的类簇,直到所有的核心对象都遍历完。
4.3层次聚类
层次聚类是一种基于树形结构的聚类方法,常用的是自底向上的结合策略(AGNES算法)。假设有N个待聚类的样本,其基本步骤是:

5、参考文献
《机器学习》周志华

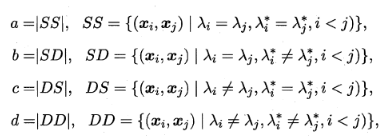

 浙公网安备 33010602011771号
浙公网安备 33010602011771号