聚类--KMeans

1、什么是K均值聚类

  • k均值聚类是最简单也是最常用的聚类算法之一。它试图找到代表数据特定区域的簇中心（Cluster Center）

  • K-means算法过程
    1.随机布置K个特征空间内的点作为初始的聚类中心
    2.对于根据每个数据的特征向量，从K个聚类中心中寻找距离最近的一个，并且把该数据标记为从属这个聚类中心
    3.在所有的数据都被标记过聚类中心之后，根据这些数据新分配的类簇，重新对K个聚类中心做计算
    4.如果一轮下来，所有的数据点从属的聚类中心与上一次的分配的类簇没有变化，那么可以迭代停止，否者回到第2步继续循环

    mglearn.plots.plot_kmeans_algorithm()


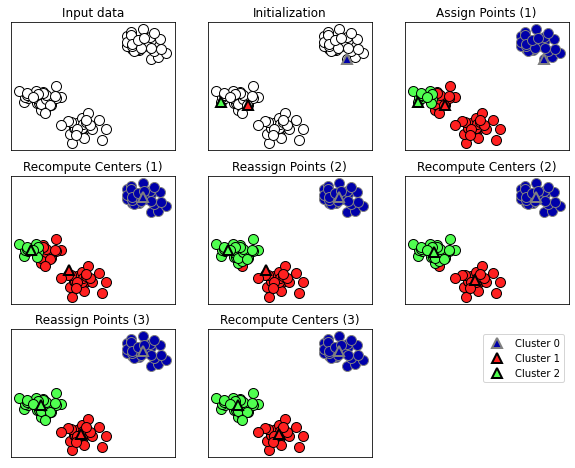
  mglearn.plots.plot_kmeans_boundaries()

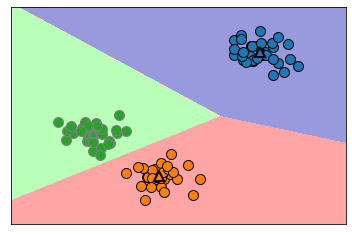
2、KMeans应用于模拟数据

  #获取数据集
  X, y = make_blobs(n_samples=100,n_features=2,random_state=42)

  #Kmeans模型实例化

  kmeans = KMeans(n_clusters=3,random_state=0)
  kmeans=kmeans.fit(X)

  #打印kmeans.labels_属性
  print("labels:{}".format(kmeans.labels_))

📣

  • ①算法运行期间，为 X 中的每个训练数据点分配一个簇标签。

    • 在 kmeans.labels_ 属性中找到这些标签：

  • ②也可以用 predict 方法为新数据点分配簇标签。

    • 预测时会将最近的簇中心分配给每个新数据点，但现有模型不会改变。
    • 对训练集运行 predict 会返回与 labels_ 相同的结果。

将上述的分类结果可视化

  mglearn.discrete_scatter(X[:,0],X[:,1],kmeans.labels_,markers='o')
  mglearn.discrete_scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],[0,1,2],markers='^',markeredgewidth=2)


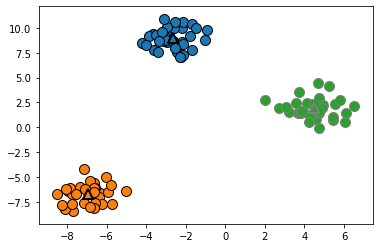
  #使用更多或更少的簇中心

  fig ,axes = plt.subplots(1,2,figsize=(10,5))

  clusters=[2,4,5]

  for c, axe in zip(clusters,axes):
      kmeans = KMeans(n_clusters=c)
      kmeans = kmeans.fit(X)
      labels = kmeans.labels_
      
      mglearn.discrete_scatter(X[:,0],X[:,1],labels,ax=axe)

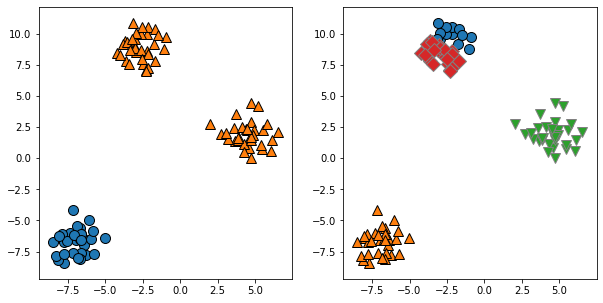
3、K均值失败的案例

对于k均值，即使给定算法正确的簇的个数，也无法保证一定可以找到正确的簇。

  • 因为每个簇仅仅是由其中心定义的，着意味着每个簇都是凸的（比如圆形）。所以k均值只能找到相对简单的形状。
  • k 均值还假设所有簇在某种程度上具有相同的“直径”，它总是将簇之间的边界刚好画 在簇中心的中间位置。

3.1 簇的密度不同

  #K均值失败的案例（密度不同or非球形簇很难识别）

  # 密度差别大的簇

  X_varied, y_varied = make_blobs(n_samples=200,
                                  cluster_std=[1.0,2.5,0.5],
                                 random_state=42)

  y_pred = KMeans(n_clusters=3,random_state=42).fit_predict(X_varied)

  mglearn.discrete_scatter(X_varied[:,0],X_varied[:,1],y_pred)

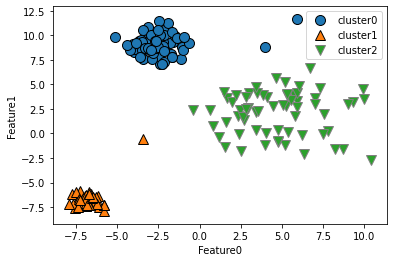
  plt.legend(["cluster0","cluster1","cluster2"],loc='best')
  plt.xlabel("Feature0")
  plt.ylabel("Feature1")

📣

我们直观地会认为，左下方的密集区域是第一个簇，右上方的密集区域是第二个，中间密度较小的区域是第三个。
但事实上，簇 0 和簇 1 都包含一些远离簇中其他点的点。

3.2 非球形簇

k 均值还假设所有方向对每个簇都同等重要。这使得它无法处理如下被沿着对角线拉长的数据集：

  #非球形簇

  import numpy as np

  #生成随机分组的数据
  X ,y = make_blobs(random_state=170,n_samples=600)
  rng = np.random.RandomState(74)

  #变换数据，将其拉长
  transformation = rng.normal(size=(2,2))
  X = np.dot(X,transformation)

  #Kmeans

  kmeans = KMeans(n_clusters=3,random_state=0).fit(X)
  y_pred = kmeans.predict(X)


  #画出分配的簇和簇中心

  mglearn.discrete_scatter(X[:,0],X[:,1],y_pred)
  mglearn.discrete_scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],[0,1,2],markeredgewidth=2)

  plt.xlabel("Feature0")
  plt.ylabel("Feature1")

📣
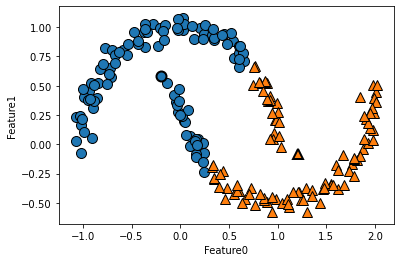
由于 k 均值仅考虑到最近簇中心的距离，所以它对上述数据集进行了错误的分类，它无法处理非球形的簇。

3.3 形状复杂的簇

如果簇的形状更加复杂，比如two_moons （sklearn.datasets自带数据集）数据，那么 k 均值的表现也很差：

  from sklearn.datasets import make_moons


  #形状复杂的数据

  #生成随机分组的数据
  X ,y = make_moons(random_state=0,n_samples=200,noise=0.05)


  #Kmeans

  kmeans = KMeans(n_clusters=2,random_state=0).fit(X)
  y_pred = kmeans.predict(X)


  #画出分配的簇和簇中心

  mglearn.discrete_scatter(X[:,0],X[:,1],y_pred)
  mglearn.discrete_scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],[0,1],markeredgewidth=2)

  plt.xlabel("Feature0")
  plt.ylabel("Feature1")

4、矢量量化（把KMeans看作分解）

虽然 k 均值是一种聚类算法，但在k均值和分解方法（PCA,NMF）之间存在一些相似之处。

  • PCA 试图找到数据中方差最大的方向
  • NMF 试图找到累加的分量
  • PCA,NMF通常对应于数据的“极值”或“部分”。试图将数据点表示为一些分量之和。

与之相反，

  • k 均值则尝试利用簇中心来表示每个数据点。
    • 你可以将其看作仅用一个分量来表示每个数据点，该分量由簇中心给出。
  • 这种 观点将 k 均值看作是一种分解方法，其中每个点用单一分量来表示，这种观点被称为矢量量化（vector quantization）

4.1并排比较PCA、NMF、KMeans

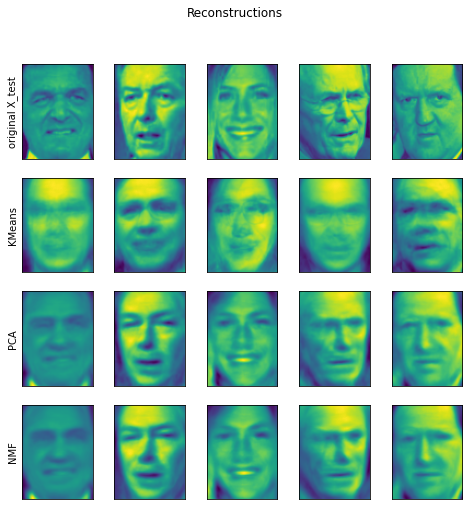
  • 分别显示提取的100个分量；并对测试集中的人脸进行重建，

  • 对于KMeans就是将测试集中的数据点找到它们最靠近的簇中心（这簇中心由训练集进行fit得到）

    #矢量量化

#PCA试图找到数据中心方差最大的方向
#NMF试图将数据点看做为几个分量之和

#Kmeans看作是一种分解方法，每个点用簇中心来表示

#比较和显示PCA,NMF,KMeans提取的分量，利用100个分量对测试集中的人脸重建

from sklearn.decomposition import PCA
from sklearn.decomposition import NMF
from sklearn.datasets import fetch_lfw_people

people = fetch_lfw_people(min_faces_per_person=20,resize=0.7)
image_shape = people.images[0].shape

# 降低数据偏斜，每个人最多取50张图像

mask = np.zeros(people.target.shape,dtype=np.bool)

for target in np.unique(people.target):
    mask[np.where(people.target==target)[0][:50]]=1 #按条件查找数组元素并返回索引——np.where()

X_people = people.data[mask] #mask是一个bool列表，将显示True的行选出来做X_people
y_people = people.target[mask]

X_people=X_people / 255 #把灰度值缩放到0-1之间

X_train,X_test,y_train,y_test=train_test_split(X_people,y_people,random_state=0)


#实例化各模型，并进行拟合
nmf = NMF(n_components=100,random_state=0).fit(X_train)
pca = PCA(n_components=100,random_state=0).fit(X_train)
kmeans = KMeans(n_clusters=100,random_state=0).fit(X_train)

#分别对测试集进行数据转化，然后重建
X_reconstruction_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstruction_nmf = np.dot(nmf.transform(X_test),nmf.components_) #为啥要点乘？
X_reconstruction_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)]


fig, axes = plt.subplots(3,5,figsize=(8,8),subplot_kw={'xticks':(),'yticks':()})

fig.suptitle("Extracted Components")

for ax, comp_kmeans, comp_pca, comp_nmf in zip(
    axes.T,kmeans.cluster_centers_,pca.components_,nmf.components_):
    ax[0].imshow(comp_kmeans.reshape(image_shape))
    ax[1].imshow(comp_pca.reshape(image_shape))
    ax[2].imshow(comp_nmf.reshape(image_shape))
    
axes[0,0].set_ylabel("KMeans簇中心的图像化")
axes[1,0].set_ylabel("PCA")
axes[2,0].set_ylabel("NMF")


fig, axes = plt.subplots(4,5,figsize=(8,8),subplot_kw={'xticks':(),'yticks':()})

fig.suptitle("Reconstructions")

for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip(
    axes.T,X_test,X_reconstruction_kmeans,X_reconstruction_pca,X_reconstruction_nmf):
    ax[0].imshow(orig.reshape(image_shape))
    ax[1].imshow(rec_kmeans.reshape(image_shape))
    ax[2].imshow(rec_pca.reshape(image_shape))
    ax[3].imshow(rec_nmf.reshape(image_shape))

axes[0,0].set_ylabel("original X_test")    
axes[1,0].set_ylabel("KMeans")
axes[2,0].set_ylabel("PCA")
axes[3,0].set_ylabel("NMF")


4.2利用KMeans的许多簇来表示复杂数据集中的变化（维数提高）

让我们回到 two_moons 数据。如果我们使用更多的簇中心，我们可以用 k 均值找到一种更具表现力的表示：

  #用KMeans的transform来给数据提升维度，得到一种表现力更强的数据表示
  #以make_moons为数据集

  from sklearn.datasets import make_moons

  X,y = make_moons(n_samples=200,noise=0.05,random_state=0)

  kmeans = KMeans(n_clusters=10).fit(X)
  y_pred = kmeans.predict(X)


  #画图表示

  plt.scatter(X[:,0],X[:,1],c=y_pred,s=60,cmap='Paired')
  plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],
              c=range(kmeans.n_clusters),s=60,linewidths=2,cmap='Paired')

📣

现在我们使用了10个簇中心，换言之，每个点现在都被分配了0到9之间的一个数字。于是我们可以构建10个新的特征 。

  • 利用这个 10 维表示，现在可以用线性模型来划分两个半月形，而利用原始的两个特征是无法做到这一点的。

👍

将到每个簇中心的距离作为特征， 还可以得到一种表更好的数据表示。

  • 可以利用 kmeans 的 transform 方法来完成这一点。

5、参考文献

《python机器学习基础教程》P130-P139

posted @ 2022-05-05 15:53  朝南烟  阅读(217)  评论(0)  编辑  收藏  举报
body { color: #000; background-color: #e6e6e6; font-family: "Helvetica Neue",Helvetica,Verdana,Arial,sans-serif; font-size: 12px; min-height: 101%; background: url(https://images.cnblogs.com/cnblogs_com/caolanying/1841633/o_2009041…ly1geq8oc9owbj21hc0u0th5.jpg) fixed; } #home { margin: 0 auto; opacity: 0.8; width: 65%; min-width: 1080px; background-color: #fff; padding: 30px; margin-top: 50px; margin-bottom: 50px; box-shadow: 0 2px 6px rgba(100, 100, 100, 0.3); }