降维、特征提取与流形学习--主成分分析

主成分分析（PCA）是一种旋转数据集的方法，旋转后的特征在统计上不相关。

1、什么是PCA

（1）、理解概念

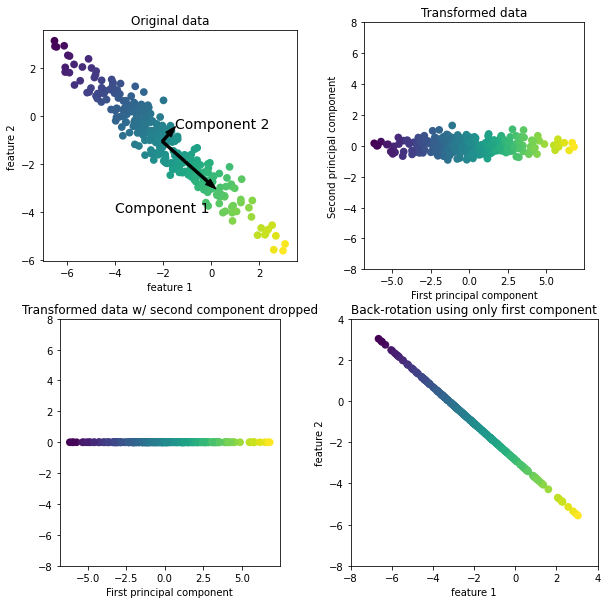
下图展示了PCA对于一个模拟二维数据集的作用

• 图一：
  算法在原始数据点集中，找到方差最大的方向（包含最多信息），标记为‘成分1’。
  找到与“成分1”正交（成直角）且包含最多信息的方向，标记为“成分2”。

  • 利用这一过程找到的方向被称为主成分（重建的最佳方向），一般主成分个数和原始特征数相同。

• 图二：从数据中减去平均值，使得变换后的数据以0为中心。

• 图三：仅保留一部分主成分（第一主成分）进行PCA降维。

• 图四：反向旋转并将平均值重新加到数据中。

（2）、主要应用

• 高维数据集可视化
• 特征提取

3、将PCA应用于cancer数据集

• 观察一下，cancer数据集中，每个特征中肿瘤类别的频次

（1）应用PCA变换

• 代码

  from sklearn.preprocessing import StandardScaler
  
  X_train, X_test,y_train,y_test=train_test_split(cancer.data,cancer.target,random_state=40)
  
  #应用pca之前，对数据进行标准化
  
  scaler = StandardScaler().fit(X_train)
  X_train_scaled = scaler.transform(X_train)
  
  #调用PCA进行降维
  
  pca = PCA(n_components=2).fit(X_train_scaled) #用训练集进行拟合
  
  print("the shape of pca components:{}".format(pca.components_.shape))
  # 可以发现主成分的shape为（2，30）说明有2个主成分，每个主成分包含所有原始特征（30个）的权重信息，权重有正有负
  
  X_train_pca = pca.transform(X_train_scaled) #对训练集进行降维，主成分为2
  
  print("Original shape:{}".format(X_train.shape))
  print("Reduced shape:{}".format(X_train_pca.shape))
  

• 输出

（2）变换后得到的主成分

-利用前两个主成分绘制乳腺癌数据集的二维散点图

  plt.figure(figsize=(8,8))
  mglearn.discrete_scatter(X_train_pca[:,0],X_train_pca[:,1],y_train)
  plt.legend(cancer.target_names,loc="best")

  #plt.gca().set_aspect("equal")

  plt.xlabel("First component")
  plt.ylabel("second component")

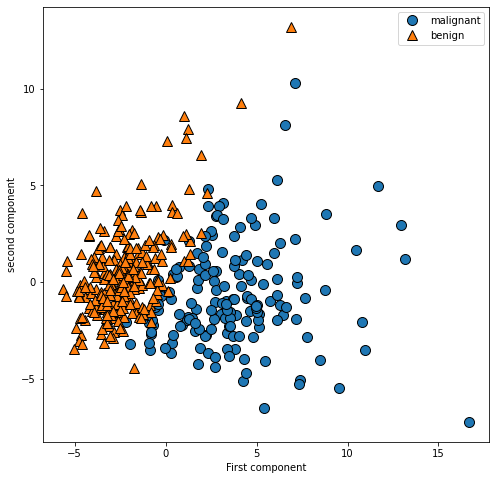
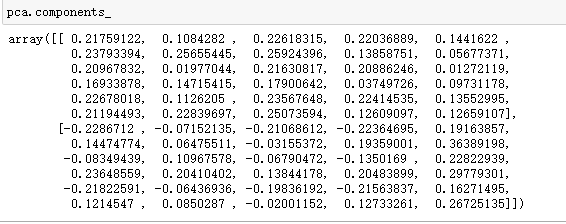
• 观察应用PCA变换后的两个主成分的属性components

• 利用热图将components进行可视化

  #利用热图将pca.components 进行可视化
  
  plt.matshow(pca.components_,cmap='viridis') #matplotlib.pyplot.matshow()画图
  
  #热图的每行，代表每个成分，有两行表示两个主成分
  #热图的每列是不同颜色的小方块，颜色深浅代表每个特征的权重大小
  
  #添加坐标轴信息
  
  plt.xticks(np.arange(len(cancer.feature_names)),cancer.feature_names,rotation=60,ha='left')
  plt.yticks([0,1],["component1","conmponent2"])
  

4、特征提取特征脸

特征提取：可以找到一种数据表示，比给定的原始数据更适合于分析。
像素值：图片的尺寸大小。
灰度值：指的是单个像素点的亮度。灰度值越大表示越亮。范围一般从0到255，白色为255 ，黑色为0。

（1）先了解一下数据集

• Wild数据集中的人脸图像
  • 这个数据集有3023张图片，每张87*65像素，分别属于62个人，每个人照片数量不等。

• 通过上述操作，我们得到了这个数据集的基本情况，并发现这个数据集有些偏斜

（2）用PCA提取特征脸，运用KNN进行评估

目标：预测某个人脸是否属于数据库中的某个已知人物。

• 方法：
  • 构建一个分类器，每个人是一个类别，但是类别的训练数据不足（同一个人图像不足），难添加新人物。
  • 使用单一近邻分类器（寻找与要分类的人脸最为相同的一个）

  mask = np.zeros(people.target.shape,dtype=np.bool)#降低数据偏斜，每个人最多取50张图像

  for target in np.unique(people.target):
      mask[np.where(people.target==target)[0][:50]]=1 #按条件查找数组元素并返回索引——np.where()

  X_people = people.data[mask] #mask是一个bool列表，将显示True的行选出来做X_people
  y_people = people.target[mask]

  X_people=X_people / 255 #把灰度值缩放到0-1之间

• 没有使用pca

  from sklearn.neighbors import KNeighborsClassifier
  
  X_train,X_test,y_train,y_test = train_test_split(X_people,y_people,random_state=0)
  
  knn = KNeighborsClassifier(n_neighbors=1).fit(X_train,y_train)
  
  print("test score:{}".format(knn.score(X_test,y_test)))
  

-输出

  test score:0.2145748987854251

📣

精度较低，因为计算原始像素空间中的距离时，如果使用像素距离，将人脸右移一个像素将会发生巨大变化，得到一个完全不同的表示。
用像素比较两张图片是，比较的是每个像素灰度值与另一张图像对应位置的像素灰度值。
于是进行处理，沿着主成分方向的距离可以提高精度↓

• 使用PCA
  启用PCA的白化选项（旋转缩放数据），将主成分缩放到相同的尺度。变换后与使用StandardScaler（每个特征的平均值为0，方差为1）相同。

  pca = PCA(n_components=100,whiten=True,random_state=0)
  pca.fit(X_train)
  #pca降维
  X_train_pca = pca.transform(X_train)
  X_test_pca = pca.transform(X_test)
  #对降维后的数据使用knn
  knn = KNeighborsClassifier(n_neighbors=1).fit(X_train_pca,y_train)
  
  print("test score:{}".format(knn.score(X_test_pca,y_test)))
  

• 输出

  test score:0.27125506072874495
  

📣

主成分可能提供了一种更好地数据表示

5、参考文献

《Pyhton机器学习基础教程》P107-P119