[C++] 分治法之棋盘覆盖、循环赛日程表

一、分治的基本思想

　　将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

　　对于一个规模为 n 的问题，若问题可以容易地解决，则直接解决，否则将其分解为 k 个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

二、用分治法求解问题的主要步骤

　　1、分解：将原问题分解为若干规模较小、相互独立、与原问题形式相同的子问题；

　　2、解决：若子问题规模较小而容易被解决则直接解决，否则，递归地解各个子问题；

　　3、合并：将各子问题的解合并得到原问题的解。

三、分治法实例

　　1、棋盘覆盖

　　在一个 2^k * 2^k 个方格组成的棋盘中，有一个方格与其它的不同，若使用以下四种 L 型骨牌覆盖除这个特殊方格的其它方格，如何覆盖。四个 L 型骨牌如下图：

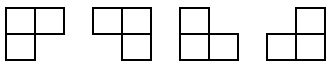
图1.1 L型骨牌

       棋盘中的特殊方格如图：

图1.2 存在特殊方格的棋盘

　　覆盖完成后的棋盘：

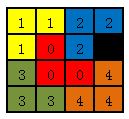
图1.3 覆盖完成的棋盘

#include<iostream>
using namespace std;

int tile = 0;
int Board[4][4];    //棋盘 

/*
tr:棋盘左上角方格的行号 
tc:棋盘左上角方格的列号
dr:特殊方格所在的行号 
dc:特殊方格所在的列号
size:棋盘的规格（size * size)
*/
void ChessBoard(int tr,int tc , int dr, int  dc, int size)
{
    if(size == 1) return;
    int t =tile++,        //L型骨牌号 
        s = size/2;        //分割棋盘 
    //覆盖左上角子棋盘 
    if(dr < tr+s && dc < tc+s)
        //特殊方格在此棋盘中 
        ChessBoard(tr,tc,dr,dc,s);
    else
    {    //此棋盘中无特殊方格
        //用t号L型骨牌覆盖右下角 
        Board[tr+s-1][tc+s-1] = t;
        //覆盖其余方格 
        ChessBoard(tr,tc,dr,dc,s);
    }
    
    //覆盖右上角子棋盘
    if(dr < tr+s && dc >= tc+s)
        //特殊方格在此棋盘中
        ChessBoard(tr,tc+s,dr,dc,s);
    else
    {    //此棋盘中无特殊方格
        //用t号L型骨牌覆盖左下角
        Board[tr+s-1][tc+s] = t;
        //覆盖其余方格 
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
    }
    
    //覆盖左下角子棋盘
    if(dr >= tr+s && dc < tc+s)
        //特殊方格在此棋盘中
        ChessBoard(tr+s,tc,dr,dc,s);
    else
    {    //此棋盘中无特殊方格
        //用t号L型骨牌覆盖右上角
        Board[tr+s][tc+s-1] = t;
        //覆盖其余方格 
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
    }
    
    //覆盖右下角子棋盘
    if(dr >= tr+s && dc >= tc+s)
        //特殊方格在此棋盘中
        ChessBoard(tr+s,tc+s,dr,dc,s);
    else
    {    //此棋盘中无特殊方格
        //用t号L型骨牌覆盖左上角
        Board[tr+s][tc+s] = t;
        //覆盖其余方格 
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
    }

}

int main()
{
    ChessBoard(0 , 0 , 1 , 3 , 4);
    //输出覆盖完成后的棋盘
    for(int i = 0 ; i < 4; i++)
    {
        for(int j = 0 ; j < 4; j++)
        {
            cout<<Board[i][j];
        }
        cout<<endl;
    }
    return 0;
}

　　2、循环赛日程表

　　设有 n = 2^k 个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表：

　　　　(1)每个选手必须与其他n-1个选手各赛一次；

　　　　(2)每个选手一天只能参赛一次；

　　　　(3)循环赛在n-1天内结束。

     请按此要求将比赛日程表设计成有 n 行和 n-1 列的一个表。在表中的第 i 行，第 j 列处填入第 i 个选手在第 j 天所遇到的选手。其中 1 ≤ i ≤ n，1 ≤ j ≤ n-1。8 个选手的比赛日程表如下图：

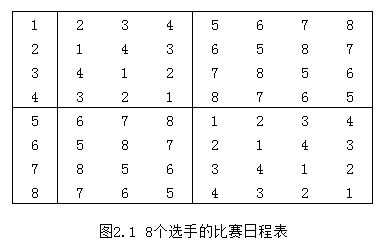
#include<iostream>
using namespace std;

int a[100][100];
int n;    //选手的个数

/*
tox:目标数组的行号 
toy:目标数组的列号 
fromx:源数组的行号 
fromy:源数组的列号 
r:数组的大小为 r*r 
*/
void Copy(int tox, int toy, int fromx, int fromy, int r)
{
    for(int i = 0; i < r; i++)
        for(int j = 0; j < r; j++)  
            a[tox+i][toy+j] = a[fromx+i][fromy+j];
}

void Table(int k)
{    
    n = 1 << k;    
    //构造正方形表格的第一行数据
    for(int i = 0; i < n; i++)
        a[0][i] = i + 1;
    //采用分治算法，构造整个循环赛日程表
    for(int r = 1; r < n; r <<= 1)
        for(int i = 0; i < n; i += 2*r)
        { 
            Copy(r, r + i, 0, i, r);        //左上角复制到右下角 
            Copy(r, i, 0, r + i, r);        //右上角复制到左下角 
        }
}


int main()
{
    int k;
    cout<<"请输入k的值：";
    cin>>k; 
    
    Table(k);
    
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            cout<< a[i][j] << " ";
        }
        cout<<endl;
    } 
    return 0;
}