2016011998+sw
Coding.net原码仓库地址:https://git.coding.net/laolaf/sw.git
目录
1 需求分析
2 功能设计
3 设计实现
4 算法详解
5 测试运行
6 满意代码
1 需求分析
用户分析:本软件的用户是小学生,因此,要对数据和算式进行限定。
限定条件总结如下:
1 数据是不超过1000的正整数;
2 运算符在3到5个之间;
3 运算过程中不能产生负数或分数(基本功能中)。
本软件具有以下功能:
1 接受参数n后可自动生成n道至少包含2种运算符的练习题,且不出现非整数或负数。
2 生成练习题后,学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中。
3 在拓展类进行复杂真分数运算。
2 功能设计:
基本功能:随机生成只有正整数的四则运算算式和答案。
扩展功能:a 支持有括号的运算式,包括出题与求解正确答案。算式中存在的括号必须大于2个,且不得超过运算符的个数。
b 扩展程序功能支持真分数的出题与运算,例如:1/6 + 1/8 + 2/3= 23/24。实现本功能时,支持运算时分数的自动化简。
模块设计:
1 Cal方法:用于转化字符串并计算得到的算式的值,支持括号运算。
2 Create方法:用于生成符合要求的算式的字符串形式。
3 Add方法:支持真分数运算的模块 。
4 main方法:输出
3 设计实现:
本软件的类:Main。主要用到了2个方法。可完成以下功能:
- 基本四则运算:功能由Cal和Create完成,由Create产生合法的(运算中不出现负数和分数)的算式,再利用Cal计算。
- 加括号的四则运算:没做。
方法:
1 Cal(String str):实现计算一个多运算符的算式。参数str即是要进行运算的字符串。在算法详解中会提到。
2 CreateQuestion(int p):实现创造一个合法的算式。参数p是运算符号的个数。
它的主体:
public static String CreateQuestion(int p) {// 产生1个包含p个运算符的四则运算的方法 String re = "";//result char oper[]={'+','-','*','÷'};//operator int Num[]=new int[30];//存储算式中的运算数 char Op[]=new char[30];//xxxxxx 运算符 for(int he=p;he>0;he--){ Op[he]=oper[(int) (Math.random()*4)]; } for(int he=p+1;he>0;he--){ Num[he]=(int) (Math.random()*100); } //谢绝野蛮连成连÷ for(int e=p;e>0;e--){ if(Op[e]=='*'||Op[e]=='÷') while(Op[e]!='*'&&Op[e]!='÷') Op[1+e]=oper[(int) (Math.random()*4)]; } //合法性问题:1 负数 2 分数. //先对乘除处理,处理之后,归纳为简单加减运算' /* 解决分数问题 */ for(int e=p;e>0;e--){ if(Op[e]=='÷') Num[e-1]*=Num[e+1]; } /*控制fu数问题,先计算已经产生的字符串,控制减数永远比被减数小,同时注意减数不能小于o*/ for(int e=0;e<p;e++){ if(Op[e] == '-') { String Caled= "" + Num[0]; for(int c=0; c<p; c++) Caled= Caled + Op[c] + Op[c+1]; int existed = Cal(Caled); Num[e+1] = existed-(int) (Math.random()*existed); }; } re=re+Num[0]; for(int pp=0;pp<p;pp++) re=re+Op[pp]+Num[pp+1]; return re;//返回一个合法的算式 }
4 算法详解
用到的主要算法是逆波兰表达式和调度场算法---用来计算字符串状态下算式的值。
参考了链接:https://liam0205.me/2016/12/14/Shunting-Yard-Algorithm/]
这里讲得很清楚了:

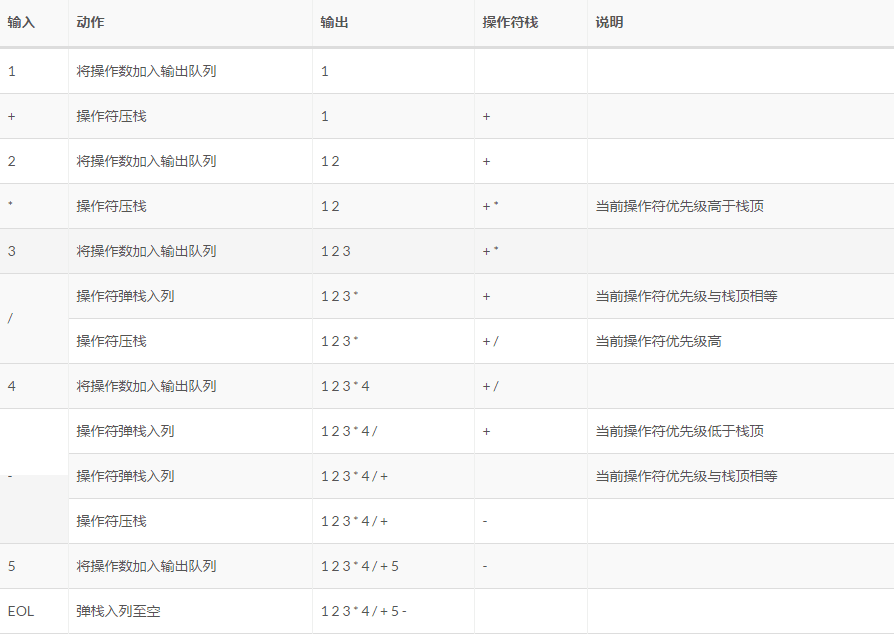
简单地说,就是先将要输入的表达式存入list中,然后,将表达式变为逆波兰表达式压入栈内,通过正则判断字符串是否为数字,是,输出到集合里,不是,则进行优先级的判断,括号的级别最高,其次是乘除,然后是加减。
部分代码:
List<String> list = (List<String>) new ArrayList<>(); Collections.addAll(list, expression); Stack<String> stack = new Stack<>(); List<String> RPNList = new ArrayList<>(); String numRegex = "^-?[0-9]+$"; for(String s : list) { if(s.matches(numRegex)) { RPNList.add(s); }else if("*".equals(s) || "/".equals(s) || "+".equals(s) || "-".equals(s)) { if(stack.isEmpty()) { stack.push(s); }else{ int currLevel = getLevel(s); String topStr = stack.peek(); int topLevel = getLevel(topStr); if (currLevel <= topLevel) { // 栈顶元素依次出栈并输出 while(!stack.isEmpty()) { // 遇到左括号退出 String peek = stack.peek(); if("(".equals(peek)) { break; } RPNList.add(stack.pop()); } } stack.push(s); } }else if("(".equals(s)) { stack.push(s); }else if(")".equals(s)) { // 栈顶元素依次出栈并输出 int length = stack.size(); for(int i = 0; i < length; i++) { String pop = stack.pop(); // 遇到左括号退出 并丢弃“”"(" if("(".equals(pop)) { break; } RPNList.add(pop); } } } // 如果栈中还有元素 弹出 if(!stack.isEmpty()) { // 栈顶元素依次出栈并输出 int length = stack.size(); for(int i = 0; i < length; i++) { RPNList.add(stack.pop()); } }
5 测试运行
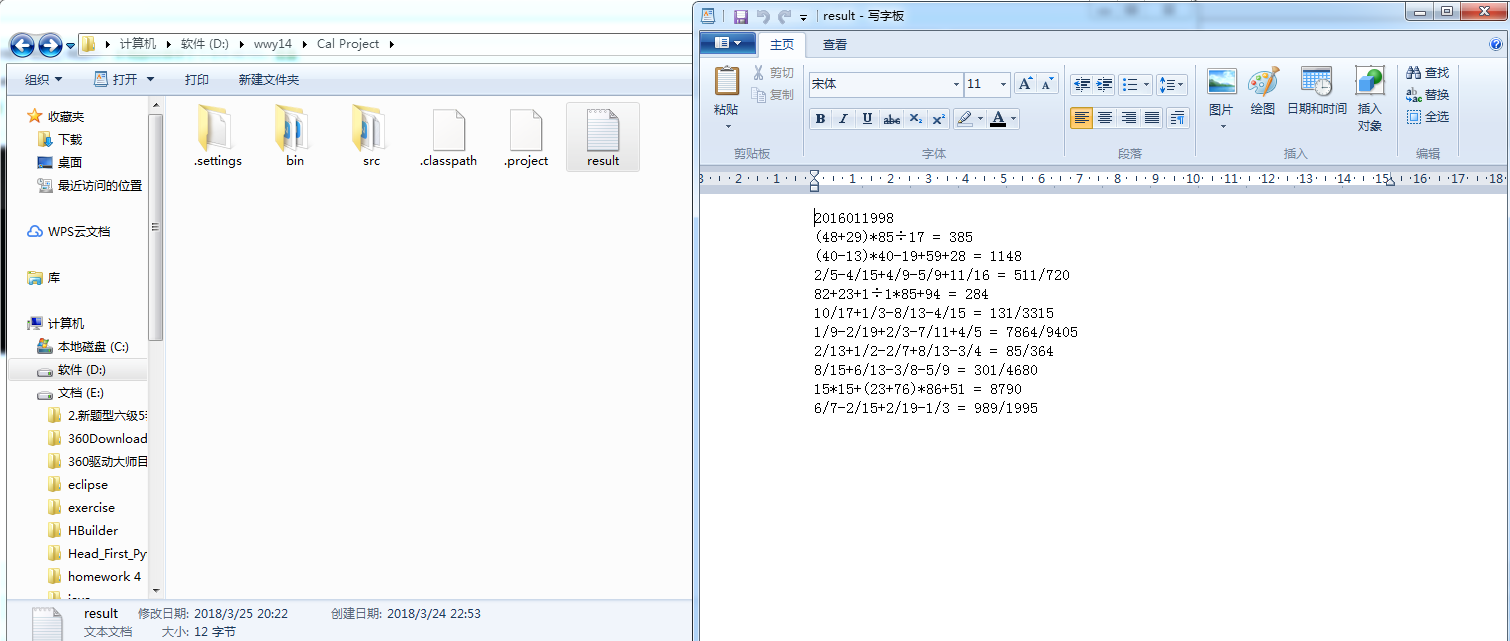
6 满意的代码:
在对算式的合法性进行控制时,对除法的控制:
//谢绝野蛮连成连÷ for(int e=0;e<p;e++){ if(Op[e]=='*'||Op[e]=='÷') Op[1+e]=oper[(int) (Math.random()*2)]; if(Op[e]!='*'&&Op[e]!='÷') Op[1+e]=oper[(int) (Math.random()*4)]; } //sffg //合法性问题:1 负数 2 分数. //先对乘除处理,处理之后,归纳为简单加减运算' /* 解决分数问题 */ for(int e=0;e<p;e++){ if(Op[e]=='÷') Num[e]=Num[e+1]*(int)(Math.random()*20); if(Op[e]=='-') { Num[e+1]=(int)(Math.random()*Num[e]/8); // Num[e+2]=(int)(Math.random()*Num[e+1]); Num[e+2]=(int)(Math.random()*4)+1; } }
首先避免了连÷(以及连*---这是防止数据过大),可以减少判断。然后,对整个算式进行搜索,发现符号为÷的,将除号前的被除数字乘上除数,这样永远不会出现未除尽的情况。
7 总结:完成这次作业最大的障碍就是语言问题,对于java过于陌生了些。另外,我觉得这次的作业还是可以体现模块化原则的,虽然我把所有的方法都写道一个类里面去了,但是功能是由各个组件独立完成的。
8 psp
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 浙公网安备 33010602011771号
浙公网安备 33010602011771号