数学——变上限积分的应用

 

 

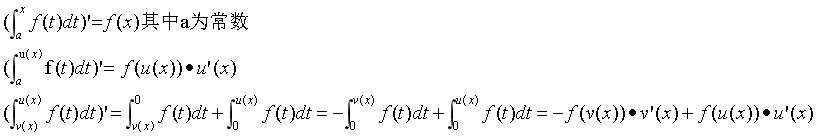
例题：

已知可导函数f(x)满足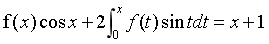，则f(x)=_____。

 

这个题中的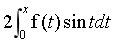部分可以用变积分上限的做法，

 

首先对原式两边分别进行求导，求导结果如下：

 

 

然后仔细观察求导之后的式子，两边同时除以(cosx)的平方，可以发现左边式子的原函数可以凑出来，方程为  ，

对这个式子进行积分，得到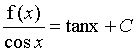

此时C是一个常数，需要把这个常数求出来，令原式中的x=0,得到f(0)=1，

 

再将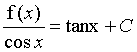式子中的x=0，得出C=1

 

最后求出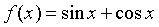

 

做这一类题目的时候，对变上限积分的求导这一知识点很容易掌握，最主要的是学会“凑”。