质点运动学、刚体力学总结
1|0质点运动学(圆周运动部分)
1|1规定
速度:
角速度:
切向、法向加速度:
角加速度:
1|2圆周运动
角加速度
切向加速度
法向加速度
如何理解?
式中为法线方向单位矢量的变化,在此基础上乘以即可得到法向向量变化。
加速度
(切向加法向)
1|3相对运动
简单解释
牵连速度是运动中的参考系的速度。想象一辆运动的火车,乘客垂直于车厢向外丢出苹果(匀速)。对于乘客,苹果的速度为。但对于地面(可以从上往下观察),苹果仍有火车的速度分量,因此将二者向量相加,得到最终。
2|0刚体转动
2|1预备知识
角速度矢量
,方向指向右手大拇指方向。
刚体上质点的运动
对于刚体上一点,有:
刚体上角速度处处相同,质点运动属性不同只与轴距有关。
2|2力矩(Moment)、力臂
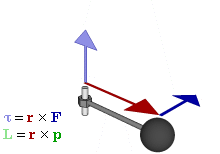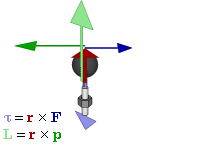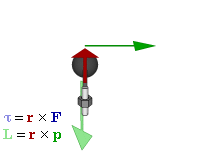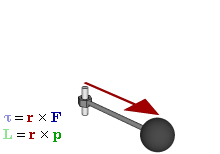
力矩等于作用于杠杆的作用力乘以支点到力的垂直距离。
——力矩 - 维基百科
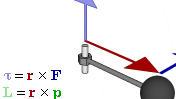
(GIF来自 力矩 - 维基百科 )
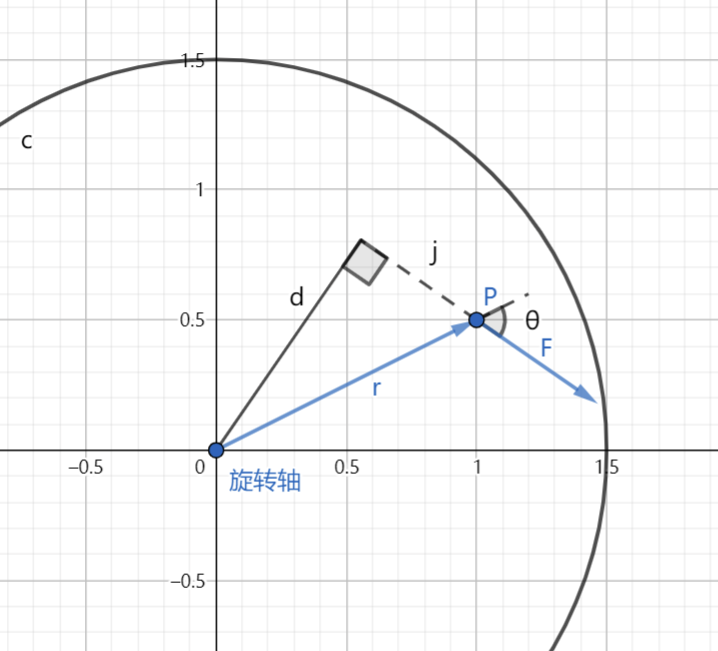
刚体上有一点,受某一外力作用,那么轴点到力直线的距离被称为力臂:
构成直角三角形:
乘以力臂就会得到力矩:
或改写为叉乘形式:
力矩是矢量,方向指向转动方向大拇指一侧。
简单介绍叉乘(矢乘)
叉乘后仍为向量;
,其中;
方向遵循右手定则,由转向大拇指方向为向量方向。;
方向垂直于平面;
有序乘法,遵循分配律。
合力矩
若刚体只有内部作用力,则这么多的内力都可以看作是一对一对的相互作用力,符合牛三。则:
那么考虑有多个外力的情况,就只需要将力矩分别求出,再求和即可:
2|3转动定律、转动惯量
转动定律又称为“角量表示下的牛顿第二定律”。
转动定律代数推导过程
不喜欢可以跳过这一段:
将刚体看作个质点连接而成的,对其中一个质点进行研究:
质点:质量,运动半径,同时受到外力、内力。
得到切向运动方程:
根据切向加速度,同时两边乘以,代入得:
再对此质点进行累计,因为内力互相抵消,所以项可以去掉。
并且注意到项即为力矩,所以最终求和后式子变为:
转动惯量(重要概念!)
上文的结尾式子,我们可以单独将项提出,并定义它为转动惯量:
因此,上文的式子也可以被改写为:
或 .
轻松理解:正如前文所说:转动定律又称为“角量表示下的牛顿第二定律”。在一般情况下,牛二的形式为,在这里我们将二者类比起来,就可以得到对应关系:
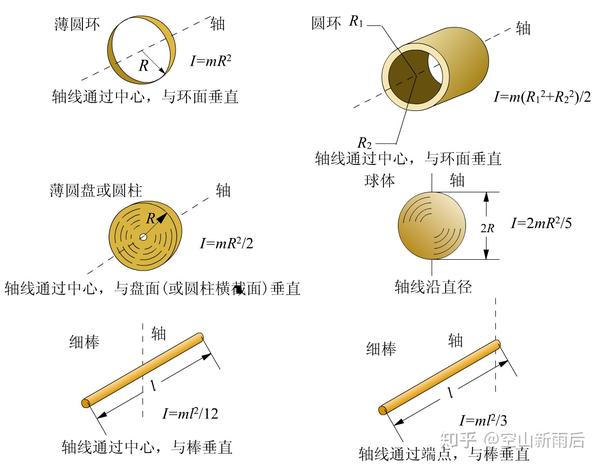
因为转动惯量并不好算,所以需要记住一些常用的物体的转动惯量:
(图片来源:【大物学习笔记(一)——刚体力学】 知乎 @空山新雨后 后文未特殊说明的图片均来源于此)
平行轴定理(巧算)
注意:刚体的转动惯量与刚体的形状、大小、质量的分布以及转轴的位置有关。 与刚体的运动状态无关。
由上可知,即使刚体不运动,任意一点的转动惯量都可以通过某种方式求得。在这里,我们使用一个过质心的轴的转动惯量作为参照。
若已经知道一个质量为刚体过质心的轴的转动惯量,则另一个离这个轴平行轴的转动惯量有这个关系:
2|4角动量守恒
角动量
质点质量为,位于坐标系内一点,据原点位矢,速度为(动量为)。定义质点角动量为:
角动量可以很轻松地与一般动量联系起来,只需要将动量叉乘质点的位矢。而在角量下,力矩代替了力,角加速度代替了加速度。
定性地理解,角动量与物体半径、质量、线速度成正比
冲量矩
对应地,冲量矩也可以很容易地定义出来:
角动量守恒定理
类比理解:系统所受合外力矩为时,角动量守恒。
当力矩为时,角动量不随时间的变化而变化,角动量为常矢量。(当合外力为时,动量不随时间的变化而变化)并且合外力或与共线。
在某一时间段内,作用在刚体上的外力的冲量矩等于刚体的角动量增量。(力矩对时间的积分就是冲量矩,角动量变化量就是角动量的增量)
经典情形
人体旋转时张开手臂与聚拢手臂,角速度不同。
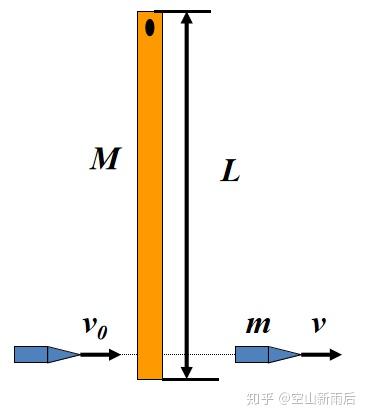
质量为的子弹以打在单边固定的质量为的木棍上,以速度穿出。木棍长(碰撞时间极短):
对子弹分析:,为负数,做负功。碰撞时间极短可知,再将作用在木棍上可得:
因为碰撞时间极短,又可近似为,原式可变为:
2|5(角)动能定理
功
力矩让刚体发生旋转力让物体发生位移
功率
转动动能
单个质点的动能:
求和到整个刚体:
观察到是转动惯量:
机械能守恒定律
与传统平动的公式差别不大,(一般在没有摩擦的情况可以简化为)重力势能+动能守恒:
其中可以用计算。
对于固定一段另一端自由下落的题型,可以使用作为主方程进行计算。
2|6对比记忆
感谢 知乎@空山新雨后 的图片。如有侵权,请联系我删除。
__EOF__

本文链接:https://www.cnblogs.com/canisidea/p/physics_moment.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

 总结了质点运动学、刚体力学与高中物理割裂的知识点。
总结了质点运动学、刚体力学与高中物理割裂的知识点。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通