[01] 离散型随机变量基础
前言
>看见统计-看得见的统计概率入门
这个网站很适合对概率论一点基础都没有的人快速掌握大概内容,有基础的人也可以作为可视化辅助理解。
文中包含部分网页截图,如侵犯权益请联系我,我将立即删除。
概念
随机变量
在一个试验的概率模型之下,随机变量是试验结果的实值函数,随机变量的函数定义了另一个随机变量。若一个随机变量的值域(取值范围)为一个有限集合或最多为可数无限集合,则称这个随机变量为离散的。
这个概念看看就行。
分布函数
可以理解为一堆小球随机分布在x轴上,然后从左到右数小球。这个点的函数值 = 从左到右积累起来的小球个数。
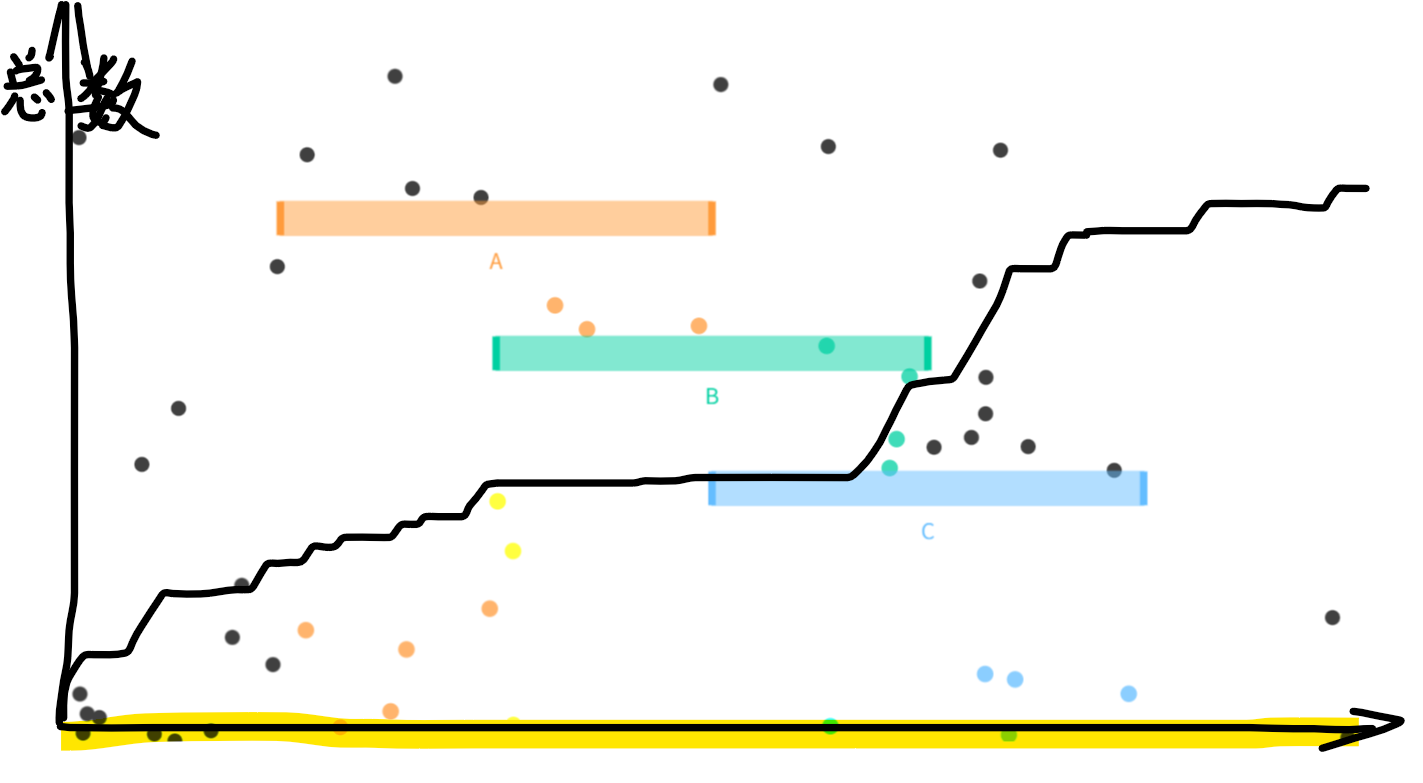
默认条件:
$ 0<F(x)<1 $
$ F(+\infty)=1 $
密度函数
是分布函数的导数,表示了这个点的概率密度。
可以理解为上面小球的密度函数。

默认条件:
$ \int_{-\infty}^{+\infty}f(x)\mathrm{d}x=1 $
概率
在 \(F(x)\) 概率模型内,\(x_1<x<x_2\) 事件发生的概率:
分布函数大减小,或者密度函数定积分。
期望(加权平均值)
一个随机变量的期望刻画的是这个随机变量的概率分布的“中心”。简而言之,当有无穷多来自同一个概率分布的独立样本时,它们的平均值就是期望。数学上对期望的定义是以概率(或密度)为权重的加权平均值。
随机变量的期望刻画了它的概率分布的“中心” 。

例如:扔一个骰子,每一面出现的概率相等,均为\(P(x)=\frac{1}{6}\)。而骰子共有1-6共六种点数,则其加权平均数为:
即:
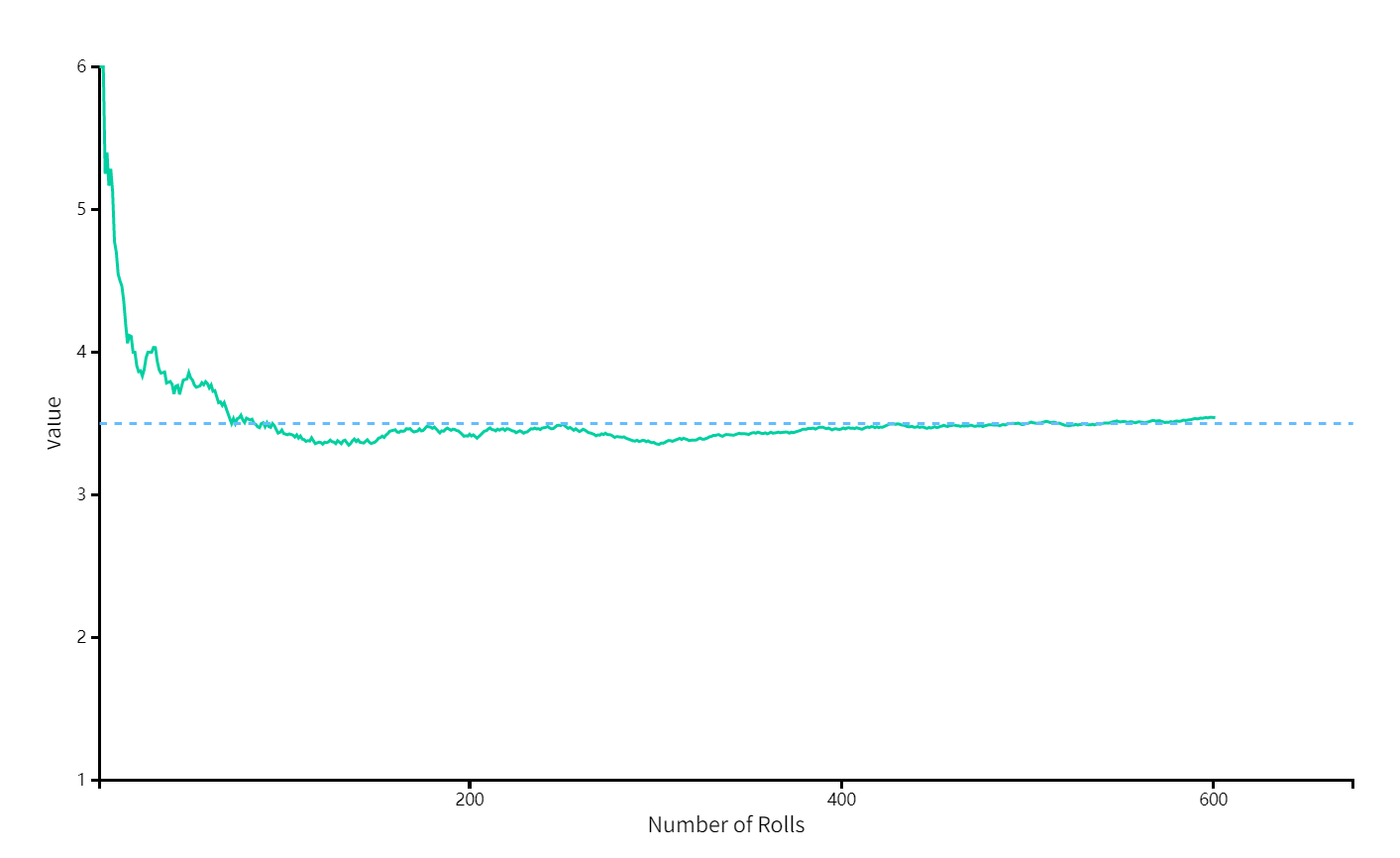
大数定理:当试验的次数越来越多时,扔出的结果的平均值慢慢趋向于它的期望\(3.5\)。如图:
当骰子质量分布变得不均匀,也就是每个面出现的概率变化的时候,点数的期望也会随之改变。
方差
方差的定义是一个随机变量与它的期望之间的差的平方的加权平均值。这里的权重仍然是概率(或者密度)。
方差刻画了概率分布的分散度,方差越小越稳定。
公式推理
数字层面的方差我们在高中就已经学过。若一系列数的平均数为\(a\),则方差可求得为:
\(s^2 = \frac{1}{n}\sum(x-a)^2\)
分析一下成分:\(a\)是整个模型中的平均数(期望),\((x-a)^2\)是每个情况和平均数之间的差,\(\frac{1}{n}\)是每个元素出现的可能性。整个式子是在求\((x-a)^2\)的平均值。
注意看:数字层面的方差可以统一乘\(\frac{1}{n}\)是因为:因为每一个数字的出现都是等可能的,所以权重是相等的,因此可以提取公因式。但是在概率中,这些情况们不再是等可能的了,因此我们需要单独求出每一个的权重。
因此类推一下:概率分布的方差就是\((x-a)^2\)的均值,即\(E(x-a)^2\),但是这里的平均值\(a\)替换为了加权平均值:\(E(x)\)。因此可得概率的方差公式:
这里的\(P\)就是每一个情况下独立的“\(\frac{1}{n}\)”。
按照骰子的情况再来理解一遍:
期望是\(3.5\),当\(X=1\),\((1-3.5)^2=6.25\)。因为出现1的概率为\(\frac{1}{6}\),所以加权求得\([X-E(x)]^2P=6.25\times\frac{1}{6}\approx 1.04\),随后对每一个情况进行计算并求和,即可算出概率的方差。
分布律
全称为:离散型随机变量的概率分布
例:X可能取值1,2,3:\(P(X=1)=\frac{1}{2}, P(X=2)=\frac{1}{4}, P(X=3)=\frac{1}{4}\)
概率分布图
表格版:
| \(X\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|
| \(P\) | \(\frac{1}{2}\) | \(\frac{1}{4}\) | \(\frac{1}{4}\) |
矩阵版:
$ X\sim \begin{pmatrix}1&2&3\\ \frac{1}{2}&\frac{1}{4}&\frac{1}{4}\end{pmatrix} $
概率分布表
是散点图:
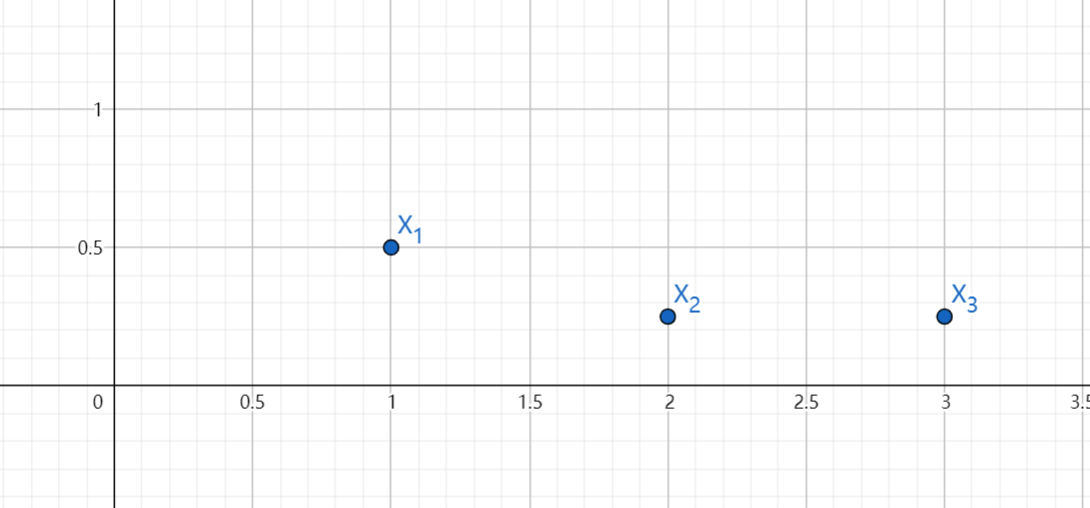
默认条件:
概率和为1:\(P(X_1)+P(X_2)+\cdots+P(x_n)=1\)
常见分布
必须有的理解
任何分布概率的积分都等于1!用来做题很方便。
伯努利分布(0-1分布)
只有0和1两种情况的分布。如新生儿性别登记,产品是否合格,丢硬币的正反等
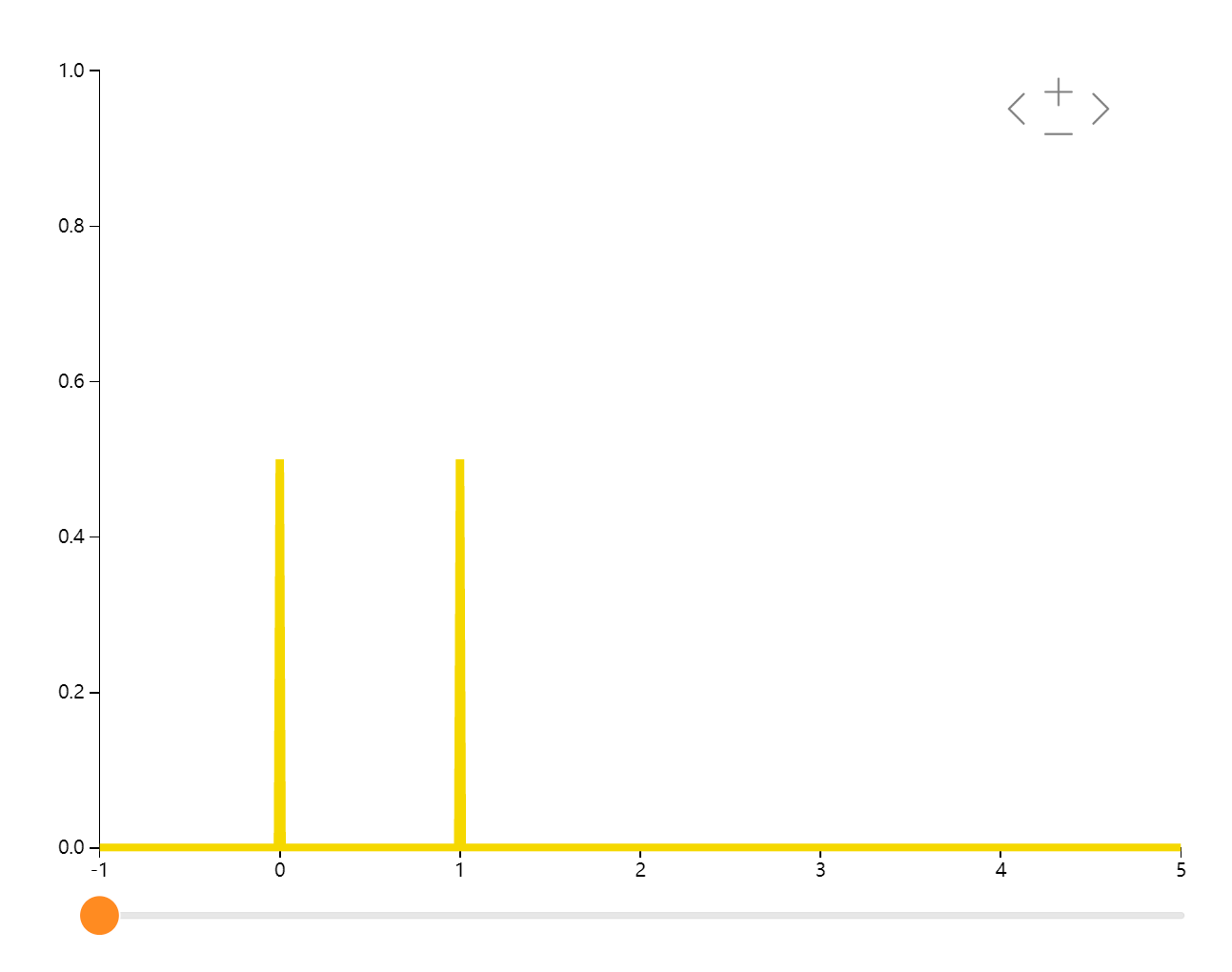
\(f(x)=\left\{\begin{matrix}p \\1-p\end{matrix}\right.\begin{matrix}\mathrm{if} x=1 \\\mathrm{if} x=0\end{matrix}\)
二项分布
多次进行伯努利试验即可得到二项分布。如:连续抛5次硬币,出现正面的概率
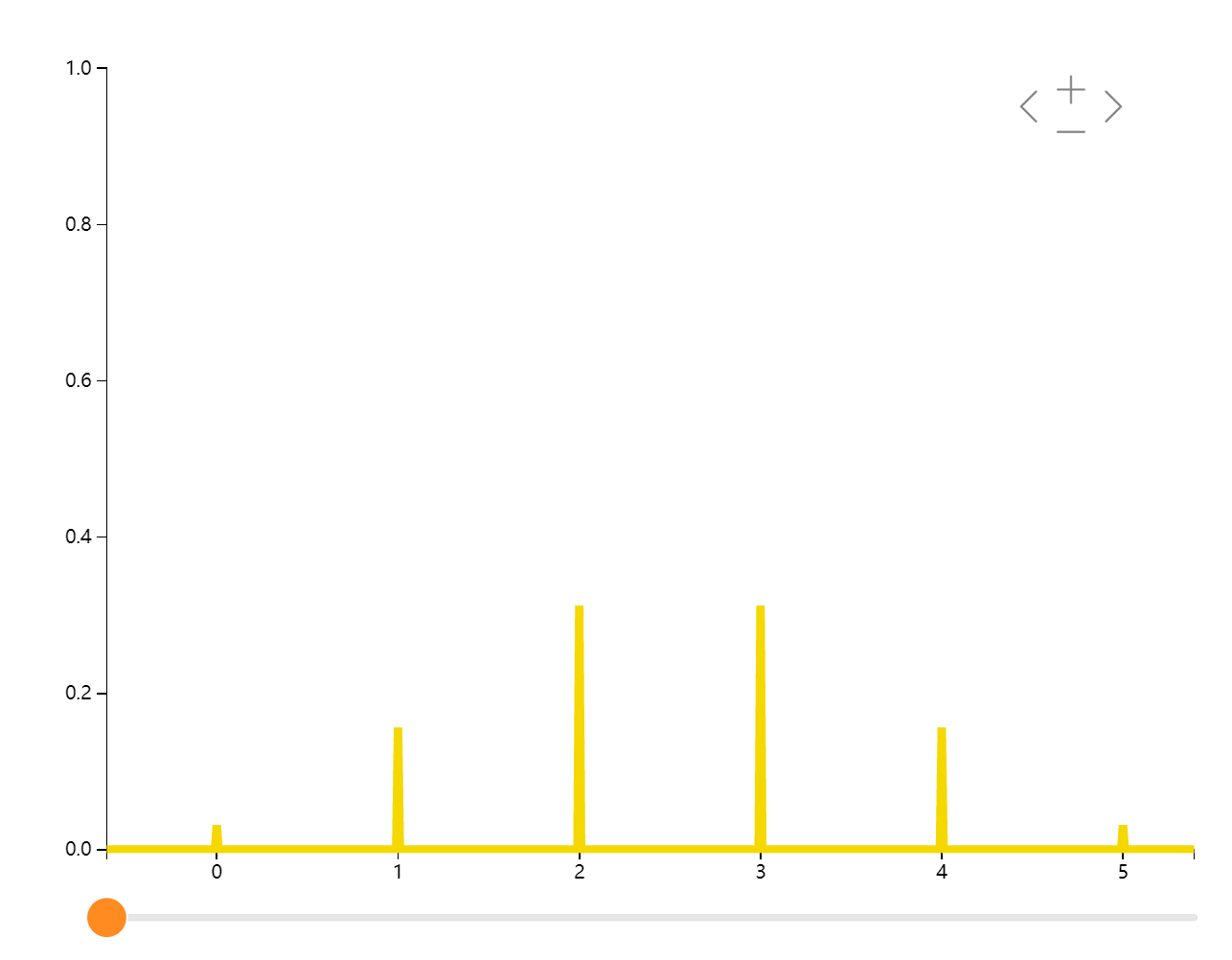
\(f(x)= C_n^k p^x(1−p)^{n−x}, (k=0,1,\cdots n)\)
若完成事件A的概率为p,共进行n次实验,则该二项分布可记为:
\(X \sim A(n, p)\)
泊松分布
当二项分布的n(试验次数)很大时,给出具体结果十分困难。但如果p很小,泊松给出了一种逼近方法:

$f(X)=\frac{\lambda ^k}{k!} e^{-\lambda } $
其中\(\lambda\)为泊松分布参数。
显然:
$\sum_{i=0}^{\infty } \frac{\lambda ^k}{k!} e^{-\lambda }=1 \Longrightarrow e^{-\lambda }\sum_{i=0}^{\infty } \frac{\lambda ^k}{k!} \Longrightarrow e^{-\lambda }e^{\lambda } =1 $ (这里的无穷级数求和比较常用,可以记一下)
如:牧草杂草种子数,物体表面细菌数,电话交换台收到呼叫次数等。实际使用中,我们使用泊松分布来近似表示二项分布。
对于实际的概率计算,我们可利用编好的泊松分布数值表直接查得。
超几何分布
高中知识:有N件商品,其中M件为次品,从中抽取n件,抽出次品数为X的概率为:
$P \left \{ X=k \right \} = \frac{C_{M}^{K} C_{N-M}^{n-K}} {C_{N}^{n}} , (k=0,1,2\cdots l) $,其中 \(l\) 为M和N的最小值。
超几何分布产生于不放回抽样试验(常见于产品检验),从而每次抽取时,优质品率都不一样。
若放回,则优质品率一样。
几何分布
若一件事有且只有两种结果(行或者不行),然后进行重复实验,直到发生一种结果(行)。设\(X\)为试验次数,其分布律为:
\(P \left \{ X = k \right \} = p ( 1 − p)^{k−1} ,(k = 1,2,\cdots)\)
例如:每100人中有2个AB型血,求第一次找到合格人所需的次数X的分布律。
几何分布无记忆性。
下一章节:[02] 连续型随机变量基础


