三重积分笔记

前言

多元微积分，积分部合集，Sal Khan讲授 p20-p22三元函数笔记。

这里不过多涉及详细的计算细节，侧重于三重积分的几何直觉。截图均来自视频。

直觉

根据一重积分、二重积分，很容易想到三重积分的微元是长宽高为$\mathrm{d}x,\mathrm{d}y,\mathrm{d}z$的小立方体。我们称之为$\mathrm dv$。

接着我们将这个小立方体连续地在$z,y,x$方向上进行积分：

$\int_x\int_y\int_z\mathrm{d}x\mathrm{d}y\mathrm{d}z$

得到了目标体积。

延申直觉

如果我们想要得到这一块体积的质量？密度甚至可能有变化？

假设该体积的密度符合一个函数：$\rho(x,y,z) = xyz$，如何求出其质量？

质量微分：

$\mathrm d m=（xyz）\mathrm d V$

$\mathrm d m=（xyz）（\mathrm dx\mathrm dy\mathrm dz ）$

再将其积分。

---

简单计算例题

书接上文，如何计算那一块体积的质量？

$\int_0^3\int_0^4\int_0^2xyz\cdot\mathrm dz\mathrm dy\mathrm dx$（给出了数据）

对$z$积分：$\int_0^3\int_0^4[\frac{xyz^2}{2}]^2_0\cdot\mathrm dy\mathrm dx=\int_0^3\int_0^42xy\cdot\mathrm dy\mathrm dx$

对$y$积分：$\int_0^3[xy^2]^4_0\cdot\mathrm dx=\int_0^3 16x\cdot\mathrm dx$

对$x$积分：$[8x^2]^3_0=72$

---

进阶计算例题

问题

当式子变得有些复杂的时候，应该如何去做？

给出方程：$2x+3z+y=6$，只看第一卦限的图案：

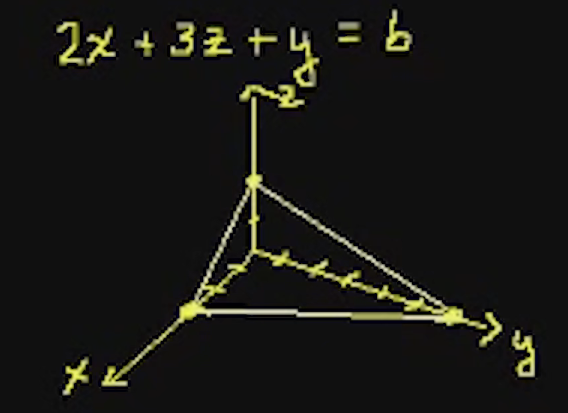
且密度可变：$\rho (x,y,z)=x^2yz$（随意取的）

找到：平面以上的体积/质量

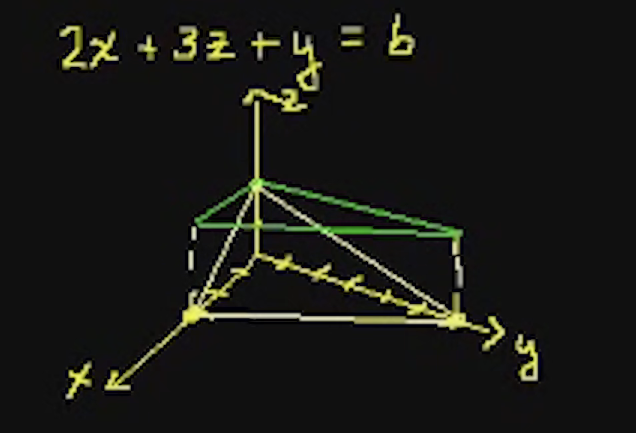
解决

考虑一个小方块$\begin{matrix} \mathrm dV=\mathrm{d}x\mathrm{d}y\mathrm{d}z \\ \mathrm dM = x^2yz\cdot\mathrm{d}x\mathrm{d}y\mathrm{d}z\end{matrix}$（顺序可变）

找到底部边界$(z)$

方程变为：$z=2-\frac{2}{3}x-\frac{1}{3}y$

积分变为：

$\int_{z=2-\frac{2}{3}x-\frac{1}{3}y}^{z=2}x^2yz\cdot \mathrm{d}z\mathrm{d}x $

从上往下看$(x,y)$

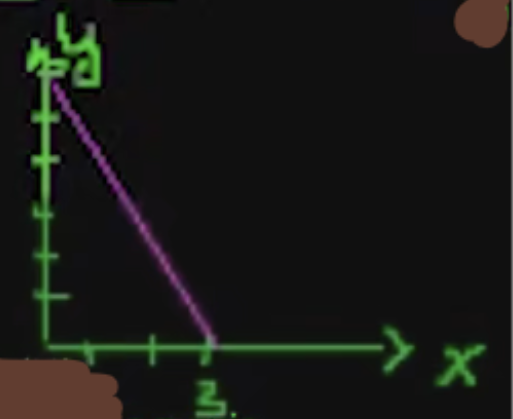
对于$z=0$的平面，方程变为$x=3-\frac{1}{2}y$

积分变为：

$\int_{x=0}^{x=3-\frac{1}{2}y}\int_{z=2-\frac{2}{3}x-\frac{1}{3}y}^{z=2} x^2yz\cdot \mathrm{d}z\mathrm{d}x $

相对于$y$轴移动，底部边界为0，上限为6/p>

积分变为：

$\int_{y=0}^{y=6}\int_{x=0}^{x=3-\frac{1}{2}y}\int_{z=2-\frac{2}{3}x-\frac{1}{3}y}^{z=2} x^2yz\cdot \mathrm{d}z\mathrm{d}x $