极坐标下的二重积分

前言

【MIT公开课】多重变量微积分 p17学习笔记（二重积分）

极坐标基础

元

半径 $r$ 和角度 $\theta$.

$\left \{\begin{matrix}x = r \cos\theta \\y = r \sin\theta\end{matrix} \right. $.

视觉理解（夸大化）

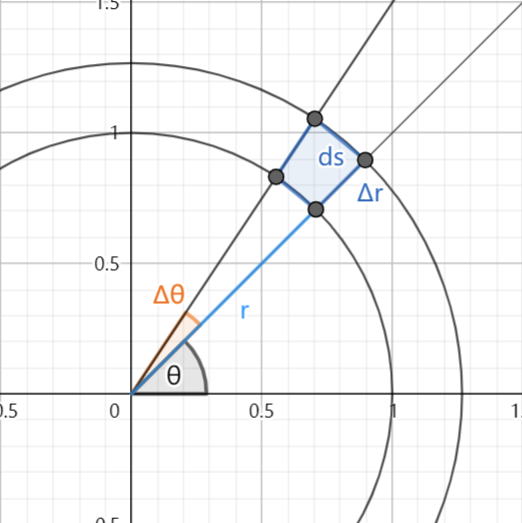
微小面积由一般的网格$\mathrm{d}y\cdot \mathrm{d}x$变为了如图扇环面积。

注意：量取$r\Delta\theta$时考虑的是“内侧”的边长，但内外侧在极小情况下等价。

微元，看作矩形求解

$\mathrm{d}s = x\cdot y= (\Delta r) \cdot (r\Delta\theta)=r\mathrm{d}r\mathrm{d}\theta$.

极坐标积分过程

给出函数

$f = 1-x^2-y^2$

转换到极坐标

$\begin{matrix}f = 1-{(r\cos\theta)}^2-{(r\sin\theta)}^2\\f=1-2r^2 \end{matrix}$

添加微元，开始积分

$\int_{0}^{\frac{\pi}{2} }\int_{0}^{1}(1-r^2)r\mathrm{d}r\mathrm{d}\theta $

（未写出原题目）

计算得到答案

$\frac{\pi}{8}$.

技巧

一般先对$r$积分，在给定的$\theta$情况下找出区域$r$的上下限。

思考（奇怪的点）

为什么极坐标的二重积分只是计算“面积”而不是一般二重积分的“体积”？

二重积分实际上指的是两个方向（元）的信息的积分。事实上面积，体积，质量都可以变成二重积分。之前我们对于二重积分的体积直觉其实是固定了一个方向的积分（直线边界）。想到这个问题说明对二重积分有了比较深刻的认识。

引出二重积分的应用：

1. 求面积

计算整个区域面积微元$\mathrm{d}s$的总和：

$S(R)=\int\int_{R}1\mathrm{d}s$

原理：将1想象为高，$\mathrm{d}s$积分则为面积，此情况下体积与面积数值相等

2. 求平面物体的质量

密度乘以面积，密度可能不均匀。

$\left\{\begin{matrix} \Delta m=\rho\cdot\Delta S\\M=\int\int_R\rho\cdot \mathrm{d}S\end{matrix}\right.$

3. 求区域平均值（等权平均值）

思想：对集合进行积分，再除以集合的大小

$\bar{f} =\frac{1}{Area(R)} \int\int_Rf\mathrm{d}S$

4. 加权平均值

与质量代替面积思维方式类似。

$\bar{f'} =\frac{1}{Mass(R)} \int\int_Rf\rho \mathrm{d}S $

这里的$\rho$就可以理解为权重（密度），除以总权（总质量）就可以求得加权平均值。

5. 物理学

将物体等效于重心。力学角度下，物体与重心等价。

---

后面的应用都与物理有关。。。我考虑一下放在大学物理分类里面