可逆矩阵与伴随矩阵
1|0前言
可逆矩阵与伴随矩阵在线性代数中密不可分。在题目中也是一大难点。因此写下这篇文章记录刷题时遇到的重要知识点。
2|0规定
1. 此文章中A矩阵默认为n阶可逆方阵;
2. 或
:为A矩阵的行列式,本文更侧重使用符合国内教材的后者;
3|0性质
3|1基本条目
1. ;
2. ;
3. ;
4. .
注意
a.) 第2条的公式右侧为逆序写出。(运算时仍是从右至左)
b.) 对于第二条,由于AB可替换为任何矩阵组。因此括号内不管有多少项,都请逆序写出。
c.) 第2条公式中的 "-1次方" 可以替换为 "*" 。也就是说此性质对于伴随矩阵同样适用。
d.) 条目不完整,略去了我认为完全符合直觉的性质。需要更多参考?点击跳转到维基百科
3|2进阶条目
如何记忆?
a.) 一次伴随矩阵操作将对所有位置进行一次代数余子式的消除。因此可以记忆为每一项最后都剩下n-1的大小。
b.) 第6条可以类似记忆。两次伴随矩阵则剩下n-2。因为没有取行列式,答案仍为矩阵,因此在最后再次乘上原矩阵A。
c.) 第7条可以理解为第4条的拓展。此处将其单独列举出来。
4|0技巧
4|1求逆矩阵
解析:
4|2判断是否可逆
配方,分解因式,加E。相比于直接求,这种类型的配凑步骤比较考验技巧。
解析:
4|3求二阶矩阵的伴随矩阵
解析:
正对角交换,反对角变号。
5|0易错点
1. 伴随矩阵是转置过的。很多教材将这一点隐藏在了公式里面,导致许多自学初学者(或者上课没有仔细听的同学)绕了弯路。根据维基百科:
......可以定义:矩阵A的伴随矩阵是A的余子矩阵的转置矩阵:
解析:
A选项:AB矩阵只是可逆,不一定相等,乘法交换后不一定相等。其余选项中只有C是书中给出的定义。尽管不知道其他的为啥错,选C就完事。(仅限应付机考)
__EOF__

本文作者:canis's idea
本文链接:https://www.cnblogs.com/canisidea/p/16121062.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/canisidea/p/16121062.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!


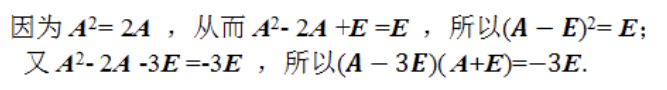



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】