洛谷 P1099 树网的核

P1099 树网的核

题目描述

设T=(V,E,W)T=(V,E,W)是一个无圈且连通的无向图（也称为无根树），每条边到有正整数的权，我们称TT为树网（treebetwork），其中VV，EE分别表示结点与边的集合，WW表示各边长度的集合，并设TT有nn个结点。

路径：树网中任何两结点aa，bb都存在唯一的一条简单路径，用d(a, b)d(a,b)表示以a, ba,b为端点的路径的长度，它是该路径上各边长度之和。我们称d(a, b)d(a,b)为a, ba,b两结点间的距离。

D(v, P)=\min\{d(v, u)\}D(v,P)=min{d(v,u)}, uu为路径PP上的结点。

树网的直径：树网中最长的路径成为树网的直径。对于给定的树网TT，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距\mathrm{ECC}(F)ECC(F)：树网T中距路径F最远的结点到路径FF的距离，即

\mathrm{ECC}(F)=\max\{d(v, F),v \in V\}ECC(F)=max{d(v,F),v∈V}

任务：对于给定的树网T=(V, E, W)T=(V,E,W)和非负整数ss，求一个路径FF，他是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过ss（可以等于s），使偏心距ECC(F)ECC(F)最小。我们称这个路径为树网T=(V, E, W)T=(V,E,W)的核（Core）。必要时，FF可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

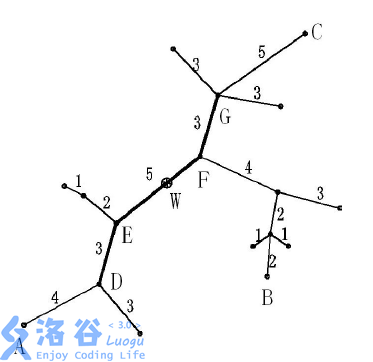
下面的图给出了树网的一个实例。图中，A-BA−B与A-CA−C是两条直径，长度均为2020。点WW是树网的中心，EFEF边的长度为55。如果指定s=11s=11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为88。如果指定s=0s=0（或s=1s=1、s=2s=2），则树网的核为结点FF，偏心距为1212。

输入输出格式

输入格式：

 

共nn行。

第11行，两个正整数nn和ss，中间用一个空格隔开。其中nn为树网结点的个数，ss为树网的核的长度的上界。设结点编号以此为1,2,…,n1,2,…,n。

从第22行到第nn行，每行给出33个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。例如，“2 4 7247”表示连接结点22与44的边的长度为77。

 

输出格式：

 

一个非负整数，为指定意义下的最小偏心距。

 

输入输出样例

输入样例#1： 复制

5 2
1 2 5
2 3 2
2 4 4
2 5 3

输出样例#1： 复制

5

输入样例#2： 复制

8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3

输出样例#2： 复制

5

说明

40\%40%的数据满足：5 \le n \le 155≤n≤15
70\%70%的数据满足：5 \le n \le 805≤n≤80
100\%100%的数据满足：5 \le n \le 300,0 \le s \le 10005≤n≤300,0≤s≤1000。边长度为不超过10001000的正整数

NOIP 2007 提高第四题

公式：一个点到a，b之间路径的距离为 (dis[i][a]+dis[i][b]-dis[a][b])/2

/*
可以想象出，这个树网的核一定在这棵树的直径上（不一定对） 
因为n很小，可以与处理出任意两点间的距离 
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 310*2
using namespace std;
int top[MAXN];
int n,s,tot,bns,ans;
int map[MAXN][MAXN];
int to[MAXN],cap[MAXN],net[MAXN],head[MAXN];
int dad[MAXN],deep[MAXN],siz[MAXN],length[MAXN];
void add(int u,int v,int w){
    to[++tot]=v;cap[tot]=w;net[tot]=head[u];head[u]=tot;
}
void dfs(int now){
    siz[now]=1;
    deep[now]=deep[dad[now]]+1;
    for(int i=head[now];i;i=net[i])
        if(dad[now]!=to[i]){
            dad[to[i]]=now;
            length[to[i]]=length[now]+cap[i];
            dfs(to[i]);
            siz[now]+=siz[to[i]];
        }
}
void dfs1(int now){
    int t=0;
    if(!top[now])    top[now]=now;
    for(int i=head[now];i;i=net[i])
        if(dad[now]!=to[i]&&siz[to[i]]>siz[now])
            t=to[i];
    if(t){
        top[t]=top[now];
        dfs1(t); 
    }
    for(int i=head[now];i;i=net[i])
        if(dad[now]!=to[i]&&t!=to[i])
            dfs1(to[i]);
}
int lca(int x,int y){
    for(;top[x]!=top[y];){
        if(deep[top[x]]<deep[top[y]])
            swap(x,y);
        x=dad[top[x]];
    }
    if(deep[x]>deep[y])    swap(x,y);
    return x;
}
int dfs2(int u,int v,int now){
    int fa=lca(u,v),cns=0x7f7f7f7f;
    for(int i=u;i!=fa;i=dad[i])
        cns=min(cns,map[now][i]);
    for(int i=v;i!=fa;i=dad[i])
        cns=min(cns,map[now][i]);
    cns=min(cns,map[now][fa]);
    return cns;
}
void work(int a,int b){
    bns=0;
    if(a==b){
        for(int i=1;i<=n;i++)
            bns=max(bns,map[i][a]);
        ans=min(ans,bns);
        return ;
    }
    if(map[a][b]>s)    return;
    for(int i=1;i<=n;i++)
        bns=max(bns,dfs2(a,b,i));
    ans=min(ans,bns);
    return ;
}
int main(){
    scanf("%d%d",&n,&s);
    memset(map,0x3f,sizeof(map));
    for(int i=1;i<n;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);add(v,u,w);
        map[u][v]=map[v][u]=w;
    }
    for(int i=1;i<=n;i++)    map[i][i]=0;
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(i!=j&&i!=k&&j!=k)
                    map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
    dfs(1);dfs1(1);
    ans=0x7f7f7f7f;
    for(int i=1;i<=n;i++)
        for(int j=i;j<=n;j++)
            work(i,j);
    cout<<ans;
}

/*
可以想象出，这个树网的核一定在这棵树的直径上（不一定对） 
因为n很小，可以与处理出任意两点间的距离 
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 310*2
using namespace std;
int top[MAXN];
int n,s,tot,bns,ans;
int map[MAXN][MAXN];
int to[MAXN],cap[MAXN],net[MAXN],head[MAXN];
int dad[MAXN],deep[MAXN],siz[MAXN],length[MAXN];
void add(int u,int v,int w){
    to[++tot]=v;cap[tot]=w;net[tot]=head[u];head[u]=tot;
}
void work(int a,int b){
    bns=0;
    if(a==b){
        for(int i=1;i<=n;i++)
            bns=max(bns,map[i][a]);
        ans=min(ans,bns);
        return ;
    }
    if(map[a][b]>s)    return;
    for(int i=1;i<=n;i++)
        bns=max(bns,(map[i][a]+map[i][b]-map[a][b])/2);
    ans=min(ans,bns);
    return ;
}
int main(){
    scanf("%d%d",&n,&s);
    memset(map,0x3f,sizeof(map));
    for(int i=1;i<n;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);add(v,u,w);
        map[u][v]=map[v][u]=w;
    }
    for(int i=1;i<=n;i++)    map[i][i]=0;
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(i!=j&&i!=k&&j!=k)
                    map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
    ans=0x7f7f7f7f;
    for(int i=1;i<=n;i++)
        for(int j=i;j<=n;j++)
            work(i,j);
    cout<<ans;
}