18.9.23 PION模拟赛

U32670 小凯的数字

题目背景

NOIP2018 原创模拟题T1

NOIP DAY1 T1 or DAY 2 T1 难度

是否发现与NOIP2017 DAY1 T1 有异曲同工之妙

说明：#10,bug已修复

题目描述

小凯有一天突发奇想，写下了一串数字：l(l+1)(l+2)...(r-1)rl(l+1)(l+2)...(r−1)r

例如：l=2,r=5l=2,r=5时，数字为：23452345

l=8,r=12l=8,r=12时数字为：8910111289101112

小凯很喜欢数字9，所以他想问你他写下的数字除以9的余数是多少

例如：l=2,r=5l=2,r=5时，2345 mod 9 = 5

输入输出格式

输入格式：

 

输入格式：

第一行为数字Q,表示小凯有Q个问题

第2-Q+1行，每行两个数字 l,r 表示数字范围

 

输出格式：

 

输出格式：

对于每行的问题输出一行，一个数字，表示小凯问题的回答

 

输入输出样例

输入样例#1： 复制 
2
2 5
8 12
输出样例#1： 复制 
5
5
输入样例#2： 复制 
3
1 999
123 456
13579 24680
输出样例#2： 复制 
0
6
0

说明

样例1解释：2345 mod 9 = 5   89101112 mod 9 = 5

30% 数据满足：Q<=10;l,r<=100Q<=10;l,r<=100

50% 数据满足：Q<=100;l,r<=10000Q<=100;l,r<=10000

70% 数据满足：Q<=1000;l,r<=10^6Q<=1000;l,r<=106

100%数据满足：Q<=10000;l,0<r<=10^{12}Q<=10000;l,0<r<=1012 且 l<=rl<=r

思路：找规律。

期望 100     实际 100

但是题解是这么一堆莫名奇妙的东西。

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int T;
long long l,r;
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld",&l,&r);
        int num=0;
        if(r-l+1>9){
            int a=l%9,b=r%9;
            for(int i=a;i<=8;i++)    num+=i;
            for(int i=1;i<=b;i++)    num+=i;
        }
        else
            for(int i=l;i<=r;i++)    num+=i%9;
        cout<<num%9<<endl;
    }
}
100分

 

U38181 密室

题目背景

NOIP2018 原创模拟题 T2

NOIP DAY1 T2 or DAY2 T2 难度

题目背景改编自小说《哈利波特与密室》。

说明：#4，bug经修复，感谢：@唐子川

题目描述

密室被打开了。

哈利与罗恩进入了密室，他们发现密室由n个小室组成，所有小室编号分别为：1,2,...,n。所有小室之间有m条通道，对任意两个不同小室最多只有一条通道连接，而每通过一条通道都需要Ci 的时间。

开始时哈利与罗恩都在编号为1的小室里，他们的目标是拯救金妮和寻找日记，但是他们发现金妮和日记可能在两个不同的小室里，为了尽快发现真相，他们决定以最少的时间到达两个目标小室。但是某些小室只有会与蛇对话的人才能进入，也就是只有哈利一个人可以进入。

现在，哈利告诉你密室的结构，请你计算他们到达两个目标小室的最短时间。

输入输出格式

输入格式：

 

第一行 n,m,k 表示有n个小室m条通道，k间小室只有哈利可以进入。

第二行 k 个数，表示只有哈利可以进入的小室的编号。（若k=0，不包含该行）

接下来m行，每行3个数：a,b,c 表示a小室与b小室之间有一条需要花费c时间的通道。

最后一行，两个数 x,y 表示哈利与罗恩需要去的小室的编号

 

输出格式：

 

一行，输出一个数，表示到达两个密室的最短时间。

 

输入输出样例

输入样例#1： 复制 
6 8 1
5
1 2 3
2 3 2
1 3 4
3 4 1
4 6 5
5 6 2
1 6 6
1 5 3
4 6
输出样例#1： 复制 
5
输入样例#2： 复制 
10 13 3
3 4 10
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
6 7 10
7 8 5
8 9 10
9 10 3
10 1 2
1 9 6
3 8 10
4 6 3
6 8
输出样例#2： 复制 
16

说明

样例解释：

样例一：

哈利：1->5->6 花费时间为5

罗恩：1->3->4 花费时间为5

所以最短时间为5

样例二：

图1

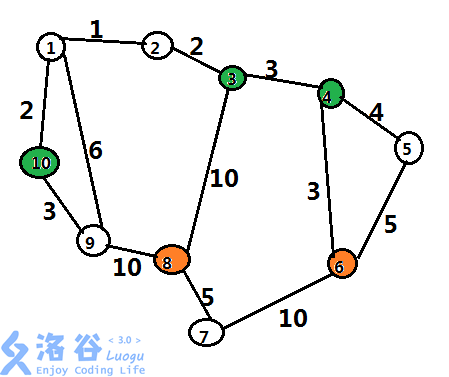
如图，橙色表示目标小室，绿色只有哈利可以通过

哈利：1->2->3->4->6 花费时间为9

罗恩：1->9->8 花费时间为16

所以最短时间为16

数据范围：

10% 数据满足：n<=5

30% 数据满足：n<=20

50% 数据满足：n<=1000

70% 数据满足：n<=10000

100%数据满足：n<=50000 ; a,b,k<=n c<=1000 ;m<=100000，保证罗恩可以在密室1

特殊约定：

30%数据满足：k=0

期望100   实际 60

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 50010
using namespace std;
int snack[MAXN];
int n,m,k,t1,t2,tot1,tot2,bns;
int vis1[MAXN],dis1[MAXN],vis2[MAXN],dis2[MAXN];
int to1[MAXN*4],cap1[MAXN*4],net1[MAXN*4],head1[MAXN];
int to2[MAXN*4],cap2[MAXN*4],net2[MAXN*4],head2[MAXN];
void add1(int u,int v,int w){
    to1[++tot1]=v;cap1[tot1]=w;net1[tot1]=head1[u];head1[u]=tot1;
}
void add2(int u,int v,int w){
    to2[++tot2]=v;cap2[tot2]=w;net2[tot2]=head2[u];head2[u]=tot2;
}
void spfa1(int s){
    queue<int>que1;
    memset(vis1,0,sizeof(vis1));
    memset(dis1,0x7f,sizeof(dis1));
    while(!que1.empty())    que1.pop();
    que1.push(s);vis1[s]=1;dis1[s]=0;
    while(!que1.empty()){
        int now=que1.front();
        que1.pop();vis1[now]=0;
        for(int i=head1[now];i;i=net1[i]){
            if(dis1[to1[i]]>dis1[now]+cap1[i]){
                dis1[to1[i]]=dis1[now]+cap1[i];
                if(!vis1[to1[i]]){
                    vis1[to1[i]]=1;
                    que1.push(to1[i]);
                }
            }
        }
    }
}
void spfa2(int s){
    queue<int>que2;
    memset(vis2,0,sizeof(vis2));
    memset(dis2,0x7f,sizeof(dis2));
    while(!que2.empty())    que2.pop();
    que2.push(s);vis2[s]=1;dis2[s]=0;
    while(!que2.empty()){
        int now=que2.front();
        que2.pop();vis2[now]=0;
        for(int i=head2[now];i;i=net2[i])
            if(dis2[to2[i]]>dis2[now]+cap2[i]){
                dis2[to2[i]]=dis2[now]+cap2[i];
                if(!vis2[to2[i]]){
                    vis2[to2[i]]=1;
                    que2.push(to2[i]);
                }
            }
    }
}
void workbns(){
    spfa1(t1);int route=dis1[t2];spfa1(1);
    bns=min(dis1[t1]+route,min(dis1[t2]+route,min(dis1[t1]*2+dis1[t2],dis1[t2]*2+dis1[t1])));
}
/*
求图上一点到另外两点的路程和最短？

思路1：求最短路生成树，然后lca求解 (不会写。。。)
思路2: 记录路径，搞一下相同的路径。
思路3：在我快写完思路2的代码时，猛然发现其实不用这样，只要求出s点到其中一点A的最短路，
       然后求A点到另一个点B的最短路，两者之和就可能是答案之一，再求s点到B点的最短路，
       加上A,B两点的最短路，和就是答案之一，然后两个答案比较，取较小的一个，即为答案。 
       (但好像并没有什么用，代码并没有AC，是60分。) 
*/
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=k;i++){
        int a;scanf("%d",&a);
        snack[a]=1;
    }    
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        if(snack[u]==1||snack[v]==1){
            add1(u,v,w);add1(u,v,w);
        }
        else {
            add1(u,v,w);add1(v,u,w);
            add2(u,v,w);add2(v,u,w);
        }
    }
    scanf("%d%d",&t1,&t2);
    spfa2(1);workbns();
    if(dis2[t1]==2139062143&&dis2[t2]==2139062143){
        cout<<bns;
        return 0;
    }
    else if(dis2[t1]==2139062143&&dis2[t2]<2139062143){
        spfa1(1);
        int ans=max(dis2[t2],dis1[t1]);
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
    else if(dis2[t2]==2139062143&&dis2[t1]<2139062143){
        spfa1(1);
        int ans=max(dis2[t1],dis1[t2]);
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
    else{
        spfa1(1);
        int ans=max(dis1[t1],dis2[t2]);
        ans=min(ans,max(dis1[t1],dis2[t1]));
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
}
60分

看了一下，发现自己的思路和题解的是一个样的，但是可能是代码写挂了，要调戏一下。

看了一下我的代码，首先是这里挂掉了

应该是酱紫的

（挂掉10）

其次是这个，有木有看出什么来？

 

建了两次同向边，应该建一个反向边。

（挂掉30）

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 50010
using namespace std;
int snack[MAXN];
int n,m,k,t1,t2,tot1,tot2,bns;
int vis1[MAXN],dis1[MAXN],vis2[MAXN],dis2[MAXN];
int to1[MAXN*4],cap1[MAXN*4],net1[MAXN*4],head1[MAXN];
int to2[MAXN*4],cap2[MAXN*4],net2[MAXN*4],head2[MAXN];
void add1(int u,int v,int w){
    to1[++tot1]=v;cap1[tot1]=w;net1[tot1]=head1[u];head1[u]=tot1;
}
void add2(int u,int v,int w){
    to2[++tot2]=v;cap2[tot2]=w;net2[tot2]=head2[u];head2[u]=tot2;
}
void spfa1(int s){
    queue<int>que1;
    memset(vis1,0,sizeof(vis1));
    memset(dis1,0x7f,sizeof(dis1));
    while(!que1.empty())    que1.pop();
    que1.push(s);vis1[s]=1;dis1[s]=0;
    while(!que1.empty()){
        int now=que1.front();
        que1.pop();vis1[now]=0;
        for(int i=head1[now];i;i=net1[i]){
            if(dis1[to1[i]]>dis1[now]+cap1[i]){
                dis1[to1[i]]=dis1[now]+cap1[i];
                if(!vis1[to1[i]]){
                    vis1[to1[i]]=1;
                    que1.push(to1[i]);
                }
            }
        }
    }
}
void spfa2(int s){
    queue<int>que2;
    memset(vis2,0,sizeof(vis2));
    memset(dis2,0x7f,sizeof(dis2));
    while(!que2.empty())    que2.pop();
    que2.push(s);vis2[s]=1;dis2[s]=0;
    while(!que2.empty()){
        int now=que2.front();
        que2.pop();vis2[now]=0;
        for(int i=head2[now];i;i=net2[i])
            if(dis2[to2[i]]>dis2[now]+cap2[i]){
                dis2[to2[i]]=dis2[now]+cap2[i];
                if(!vis2[to2[i]]){
                    vis2[to2[i]]=1;
                    que2.push(to2[i]);
                }
            }
    }
}
void workbns(){
    spfa1(t1);int route=dis1[t2];spfa1(1);
    bns=min(dis1[t1]+route,min(dis1[t2]+route,min(dis1[t1]*2+dis1[t2],dis1[t2]*2+dis1[t1])));
}
/*
求图上一点到另外两点的路程和最短？

思路1：求最短路生成树，然后lca求解 (不会写。。。)
思路2: 记录路径，搞一下相同的路径。
思路3：在我快写完思路2的代码时，猛然发现其实不用这样，只要求出s点到其中一点A的最短路，
       然后求A点到另一个点B的最短路，两者之和就可能是答案之一，再求s点到B点的最短路，
       加上A,B两点的最短路，和就是答案之一，然后两个答案比较，取较小的一个，即为答案。 
*/
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=k;i++){
        int a;scanf("%d",&a);
        snack[a]=1;
    }    
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        if(snack[u]==1||snack[v]==1){
            add1(u,v,w);add1(v,u,w);
        }
        else {
            add1(u,v,w);add1(v,u,w);
            add2(u,v,w);add2(v,u,w);
        }
    }
    scanf("%d%d",&t1,&t2);
    spfa2(1);workbns();
    spfa1(1);
    if(dis2[t1]==2139062143&&dis2[t2]==2139062143){
        cout<<bns;
        return 0;
    }
    else if(dis2[t1]==2139062143&&dis2[t2]<2139062143){
        spfa1(1);
        int ans=max(dis2[t2],dis1[t1]);
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
    else if(dis2[t2]==2139062143&&dis2[t1]<2139062143){
        spfa1(1);
        int ans=max(dis2[t1],dis1[t2]);
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
    else{
        spfa1(1);
        int ans=max(dis1[t1],dis2[t2]);
        ans=min(ans,max(dis1[t2],dis2[t1]));
        ans=min(ans,bns);
        cout<<ans<<endl;
        return 0;
    }
}
100分

所以还是要注意，本来能AC的题目，因为这挂了将近一半，从100分挂成了60分！！！！

U38098 PION贪吃蛇

题目背景

NOIP2018原创模拟题 T3

NOIP DAY1 T3 or DAY 2 T2 难度

贪吃蛇大家都玩过吧，当然不同版本有不同规则。下面介绍PION贪吃蛇。

注意：测试点#4错误已修改，感谢：@EnTaroTassadar

题目描述

图A

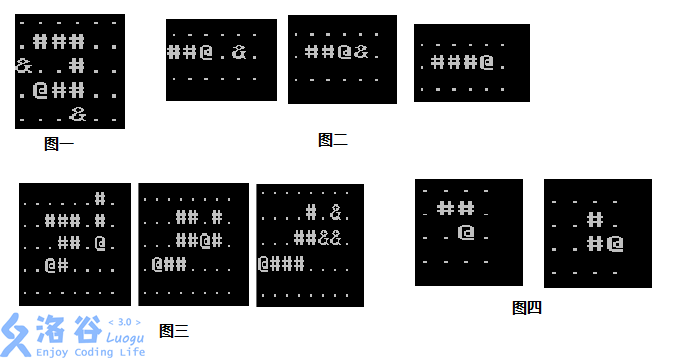
表示方法：

该题中贪吃蛇存在于一个n行m列的矩形中，用 ‘.’ 表示空地，用 '#’ 表示蛇身，用 ‘@’表示蛇头，用‘&’表示食物 例如：图一表示5*6的矩形，有一条蛇，蛇长度为7，有两个食物

基本规则：

1.蛇头每一秒就会移动一格，身体自然会跟着移动，用W表示向上，S表示向下，A表示向左，D表示向右

2.蛇每吃一个食物就长度就会加一，而增加的长度体现在食物所在的地方，你可以把吃食物理解成食物变成了蛇头，之前的蛇头变成了蛇身，这一秒不移动

例如：图二的三幅图展示了第一秒，第二秒，和第三秒的情况

3.蛇如果死亡，身体（包括头）一定会全部变成食物

4.PION贪吃蛇的蛇头碰到自己或别的蛇的身体就会死亡

例如：图三的三幅图展示了第二条蛇撞在别人身体上死亡的过程

5.蛇头撞在边界上也会引起死亡，但蛇头刚好现在边界上不会

例如：图四第二幅图虽然蛇头在边界上，但是只是刚好，如果此时进行D操作蛇就会死亡，如果进行W或S就不会

6.如果有操作使蛇头向相反方向运动，之后如果与身体重合蛇也会死亡（比如：图二第一幅图使用A操作,蛇就会死亡，此时在原地成为三个食物，你也可以理解为蛇下一秒不行动而自杀了）

7.两条蛇蛇头相撞，主动撞上的死亡

8.蛇的移动按编号由小到大进行（编号的含义见下文）

输入输出格式

输入格式：

 

第一行两个数n,m，k表示n*m的矩形，k表示操作次数

接下来n行每行m个字符，表示地图

再接下来c行（注意：图中有几条蛇就有几行），每行k个字符，表示有k个操作（如果执行了某个操作蛇死了，就忽略后面的操作）

我们将蛇编号：按每条蛇蛇头的坐标从小到大编号为1，2，...，c（越靠近上边的坐标越小，如果相同越靠近左边的坐标越小）

例如：图三第一幅图两条蛇的蛇头坐标分别为（4,3），（3,7）所以较长的蛇编号为2，较短的蛇编号为1

 

输出格式：

 

c+1行，输出k次操作后每一条蛇的长度，编号；每一行第一个为长度，第二个数为编号

最后一行输出剩下食物的总个数

注意：输出按长度由大到小排序（长度相同按编号由小到大排序），死亡的蛇长度为0

 

输入输出样例

输入样例#1： 复制 
5 7 6
.&...&.
..##@..
.&...&.
..##@..
.&...&.
DWAAAA
WDDDDD
输出样例#1： 复制 
5 1
0 2
7
输入样例#2： 复制 
9 9 4
.........
.#######.
.......#.
.@#.&@.#.
&.#.&&.#.
&&######.
.&.......
..@####..
.........
ASSD
ASDD
WASD
输出样例#2： 复制 
22 1
4 2
0 3
6

说明

样例说明：

图B

图五，图六展示了从第0秒开始之后每一秒地图的状态，请看图理解（样例二图四有点小错误）

数据范围：

10%数据满足n,m<=5,c=1,k<=3

30%数据满足n,m<=10,c<=2,k<=5

50%数据满足n,m<=50,c<=5,k<=20

70%数据满足n,m<=100,c<=7,k<=50

100%数据满足，n,m<=200,c<=20,k<=100，且图中的蛇不会引起混淆

输入保证图中没有蛇会像这样难以判断：

.#.
##@
#.#
@##

期望 0   实际 0
题目太恶心了，就没写。。。(好吧。。。其实是我懒，那暴力分应该还是可以的)


posted @ 2018-09-23 11:05  一蓑烟雨任生平  阅读(374)  评论(0)  编辑  收藏  举报