洛谷 P2951 [USACO09OPEN]捉迷藏Hide and Seek
题目描述
Bessie is playing hide and seek (a game in which a number of players hide and a single player (the seeker) attempts to find them after which various penalties and rewards are assessed; much fun usually ensues).
She is trying to figure out in which of N (2 <= N <= 20,000) barns conveniently numbered 1..N she should hide. She knows that FJ (the seeker) starts out in barn 1. All the barns are connected by M (1 <= M <= 50,000) bidirectional paths with endpoints A_i and B_i (1 <= A_i <= N; 1 <= B_i <= N; A_i != B_i); it is possible to reach any barn from any other through the paths.
Bessie decides that it will be safest to hide in the barn that has the greatest distance from barn 1 (the distance between two barns is the smallest number of paths that one must traverse to get from one to the other). Help Bessie figure out the best barn in which to hide.
奶牛贝西和农夫约翰(FJ)玩捉迷藏,现在有N个谷仓,FJ开始在第一个谷仓,贝西为了不让FJ找到她,当然要藏在距离第一个谷仓最远的那个谷仓了。现在告诉你N个谷仓,和M个两两谷仓间的“无向边”。每两个仓谷间当然会有最短路径,现在要求距离第一个谷仓(FJ那里)最远的谷仓是哪个(所谓最远就是距离第一个谷仓最大的最短路径)?如有多个则输出编号最小的。以及求这最远距离是多少,和有几个这样的谷仓距离第一个谷仓那么远。
输入输出格式
输入格式:
* Line 1: Two space-separated integers: N and M
* Lines 2..M+1: Line i+1 contains the endpoints for path i: A_i and B_i
第一行:两个整数N,M;
第2-M+1行:每行两个整数,表示端点A_i 和 B_i 间有一条无向边。
输出格式:
* Line 1: On a single line, print three space-separated integers: the index of the barn farthest from barn 1 (if there are multiple such barns, print the smallest such index), the smallest number of paths needed to reach this barn from barn 1, and the number of barns with this number of paths.
仅一行,三个整数,两两中间空格隔开。表示:距离第一个谷仓最远的谷仓编号(如有多个则输出编号最小的。),以及最远的距离,和有几个谷仓距离第一个谷仓那么远。
输入输出样例
说明
The farm layout is as follows:
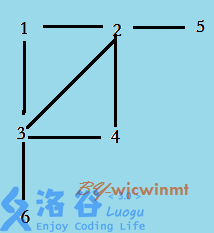
Barns 4, 5, and 6 are all a distance of 2 from barn 1. We choose barn 4 because it has the smallest index.
这里谷仓4,5,6距离1号谷仓都是2,但是4编号最小所以输出4.因此最远距离是2且有3个谷仓,依次输出:2和3。
感谢 wjcwinmt 的贡献翻译
思路:spfa的板子。
#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 124020 using namespace std; queue<int>que; int n,m,s,t=2333,tot,ans,maxn=-23333333; int vis[MAXN],num[MAXN],dis[MAXN]; int to[MAXN*2],from[MAXN],net[MAXN*2],cap[MAXN*2]; void add(int u,int v,int w){ to[++tot]=v;net[tot]=from[u];cap[tot]=w;from[u]=tot; } bool spfa(int s){ memset(vis,0,sizeof(vis)); memset(dis,0x7f,sizeof(dis)); que.push(s);dis[s]=0; vis[s]=1;num[s]++; while(!que.empty()){ int now=que.front(); que.pop(); vis[now]=0; for(int i=from[now];i;i=net[i]) if(dis[to[i]]>dis[now]+cap[i]){ dis[to[i]]=dis[now]+cap[i]; if(!vis[to[i]]){ vis[to[i]]=1; que.push(to[i]); if(++num[to[i]]>n) return false; } } } return true; } int main(){ cin>>n>>m; for(int i=1;i<=m;i++){ int u,v; cin>>u>>v; add(u,v,1); add(v,u,1); } spfa(1); for(int i=2;i<=n;++i){ if(dis[i]>maxn){ maxn=dis[i]; t=i;ans=1; } else if(dis[i]==maxn) ans++; } printf("%d %d %d",t,dis[t],ans); return 0; }


