模拟赛 Problem 2 不等数列(num.cpp/c/pas)

Problem 2 不等数列(num.cpp/c/pas)

【题目描述】

将1到n任意排列，然后在排列的每两个数之间根据他们的大小关系插入“>”和“<”。问在所有排列中，有多少个排列恰好有k个“<”。答案对2012取模。

 

【输入格式】

第一行2个整数n,k。

 

【输出格式】

一个整数表示答案。

 

【样例输入】

5 2

【样例输出】

66

【数据范围】

对于30%的数据：n <= 10

对于100%的数据：k < n <= 1000，

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 2012
#define MAXN 1010
using namespace std;
int n,k,ans;
int vis[MAXN],num[MAXN];
bool judge(){
    int bns=0;
    for(int i=2;i<=n;i++)
        if(num[i]>num[i-1])    bns++;
    if(bns==k)    return true;
    else return false;
}
void dfs(int now){
    if(now==n+1){
        if(judge())
            ans=(ans+1)%mod;
        return ;
    }
    for(int i=1;i<=n;i++)
        if(!vis[i]){
            vis[i]=1;num[now]=i;
            dfs(now+1);
            vis[i]=0;
        }
}
int main(){
    freopen("num.in","r",stdin);
    freopen("num.out","w",stdout);
    scanf("%d%d",&n,&k);
    dfs(1);
    cout<<ans<<endl;
}

打完表后会发现是一个这样的一个东西：

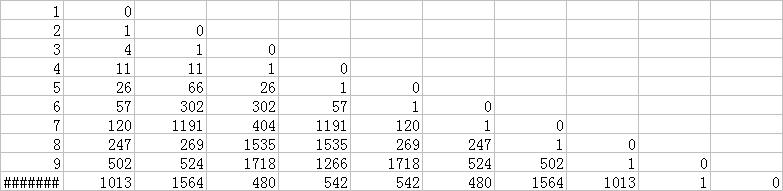
然后就可以找规律了。然后并不肿么样。

最后调转思路，转到了DP上。

f[i][j]表示在前i个里面加入j个‘<’的方案数，那么就有：

　　f[i][j]=(f[i-1][j]*(j+1)+f[i-1][j-1]*(i-j))%mod;

然后就完成了。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 2012
using namespace std;
int n,k;
int f[1001][1001];
int main(){
    freopen("num.in","r",stdin);
    freopen("num.out","w",stdout);
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)    f[i][0]=1;
    for(int i=2;i<=n;i++)
        for(int j=1;j<=min(i-1,k);j++)
            f[i][j]=(f[i-1][j]*(j+1)+f[i-1][j-1]*(i-j))%mod;
    printf("%d",f[n][k]);
}