Codeforces Round #461 (Div. 2)
Imp likes his plush toy a lot.
Recently, he found a machine that can clone plush toys. Imp knows that if he applies the machine to an original toy, he additionally gets one more original toy and one copy, and if he applies the machine to a copied toy, he gets two additional copies.
Initially, Imp has only one original toy. He wants to know if it is possible to use machine to get exactly x copied toys and y original toys? He can't throw toys away, and he can't apply the machine to a copy if he doesn't currently have any copies.
The only line contains two integers x and y (0 ≤ x, y ≤ 109) — the number of copies and the number of original toys Imp wants to get (including the initial one).
Print "Yes", if the desired configuration is possible, and "No" otherwise.
You can print each letter in arbitrary case (upper or lower).
Examples
input 6 3 output Yes
input 4 2 output No
input 1000 1001 output Yes
In the first example, Imp has to apply the machine twice to original toys and then twice to copies.
思路：注意很多特殊情况，漏掉就会gg。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int x,y; int main(){ scanf("%d%d",&x,&y); x-=(y-1); if(x==0&&y==1){ cout<<"Yes";return 0; } if(x>=0&&x%2==0&&y>1) cout<<"Yes"; else cout<<"No"; }
Imp is in a magic forest, where xorangles grow (wut?)
A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.
Formally, for a given integer n you have to find the number of such triples (a, b, c), that:
- 1 ≤ a ≤ b ≤ c ≤ n;
, where 
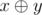denotes the bitwise xor of integers x and y.- (a, b, c) form a non-degenerate (with strictly positive area) triangle.
The only line contains a single integer n (1 ≤ n ≤ 2500).
Print the number of xorangles of order n.
Examples
input 6 output 1
input 10 output 2
The only xorangle in the first sample is (3, 5, 6).
思路：枚举即可，注意两个相同的数的抑或值为0。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,ans; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++){ int k=i^j; if(k>n) continue; if(i+j>k&&abs(i-j)<k&&i+k>j&&abs(i-k)<j&&j+k>i&&abs(j-k)<i) ans++; } cout<<ans/3; }
Imp is watching a documentary about cave painting.
Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.
Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all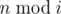 
, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:
- 1 ≤ i < j ≤ k,
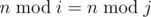, where 
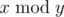is the remainder of division x by y.
Input
The only line contains two integers n, k (1 ≤ n, k ≤ 1018).
Output
Print "Yes", if all the remainders are distinct, and "No" otherwise.
You can print each letter in arbitrary case (lower or upper).
Examples
input 4 4 output No
input 5 3 output Yes
In the first sample remainders modulo 1 and 4 coincide.
思路：正序顺序枚举就可以了。
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int vis[1000000]; long long n,k; int main(){ cin>>n>>k; for(int i=1;i<=k;i++){ int m=n%i; if(!vis[m]) vis[m]=1; else{ cout<<"No";return 0; } } cout<<"Yes"; }
Apart from plush toys, Imp is a huge fan of little yellow birds!
To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him costi points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.
Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?
The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.
The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that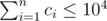 
.
The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.
Print a single integer — the maximum number of birds Imp can summon.
Examples
input 2 12 0 4 3 4 4 2 output 6
input 4 1000 10 35 1 2 4 5 1000 500 250 200 output 5
input 2 10 7 11 2 10 6 1 output 11
In the first sample base amount of Imp's mana is equal to 12 (with maximum capacity also equal to 12). After he summons two birds from the first nest, he loses 8 mana points, although his maximum capacity will not increase (since B = 0). After this step his mana will be 4 of12; during the move you will replenish 4 mana points, and hence own 8 mana out of 12 possible. Now it's optimal to take 4 birds from the second nest and spend 8 mana. The final answer will be — 6.
In the second sample the base amount of mana is equal to 1000. The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.
题意：给几颗树（有顺序），树上有ci只鸟，把第i颗树的鸟打下来要花费体力costi。人从第一颗树往后走，每走过一棵树体力上限增加B，同时体力也会回复X。问最多能打多少只鸟。
思路：背包，f[i][j]表示到第i个鸟巢为止，有j个小鸟，剩余最多的价值是几。
状态转移方程很显然就出来了：f[i][j]=max(f[i][j],min(f[i-1][j-k]+x,b*(j-k)+w)-cost[i]*k)。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 1011 using namespace std; long long n,w,b,x; long long f[MAXN][10011]; long long c[MAXN],sum[MAXN],cost[MAXN]; int main(){ memset(f,-1,sizeof(f)); cin>>n>>w>>b>>x; for(long long i=1;i<=n;i++){ cin>>c[i]; sum[i]=sum[i-1]+c[i]; } for(long long i=1;i<=n;i++) cin>>cost[i]; f[0][0]=w; for(long long i=1;i<=n;i++) for(long long j=sum[i];j>=0;j--) for(long long k=c[i];k>=0;k--){ if(k>j) continue; if(f[i-1][j-k]>=0) f[i][j]=max(f[i][j],min(f[i-1][j-k]+x,b*(j-k)+w)-cost[i]*k); } for(long long i=sum[n];i>=0;i--) if(f[n][i]>=0){ cout<<i; return 0; } }
Pushok the dog has been chasing Imp for a few hours already.
Fortunately, Imp knows that Pushok is afraid of a robot vacuum cleaner.
While moving, the robot generates a string t consisting of letters 's' and 'h', that produces a lot of noise. We define noise of string t as the number of occurrences of string "sh" as a subsequence in it, in other words, the number of such pairs (i, j), that i < j and 
and 
.
The robot is off at the moment. Imp knows that it has a sequence of strings ti in its memory, and he can arbitrary change their order. When the robot is started, it generates the string t as a concatenation of these strings in the given order. The noise of the resulting string equals the noise of this concatenation.
Help Imp to find the maximum noise he can achieve by changing the order of the strings.
The first line contains a single integer n (1 ≤ n ≤ 105) — the number of strings in robot's memory.
Next n lines contain the strings t1, t2, ..., tn, one per line. It is guaranteed that the strings are non-empty, contain only English letters 's' and 'h' and their total length does not exceed 105.
Print a single integer — the maxumum possible noise Imp can achieve by changing the order of the strings.
Examples
input 4 ssh hs s hhhs output 18
input 2 h s output 1
The optimal concatenation in the first sample is ssshhshhhs.
题意：给一些由“s”和“h”组成的字符串，把这些字符串拼接起来，贡献是所有“h”前面“s”的个数的和。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; string sh; int n,l,r,sum; long long ans; string s[100001]; struct nond{ int s,h,id; }v[100001]; int cmp(nond a,nond b){ return a.s>b.s; } int cmp1(nond a,nond b){ return a.h<b.h; } int cmp2(nond a,nond b){ double x=(a.s*1.0)/(a.h*1.0); double y=(b.s*1.0)/(b.h*1.0); return x>y; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ cin>>s[i];v[i].id=i; int len=s[i].length(); for(int j=0;j<len;j++){ if(s[i][j]=='s') v[i].s++; if(s[i][j]=='h') v[i].h++; } } sort(v+1,v+1+n,cmp); for(int i=n;i>=1;i--) if(v[i].s!=0){ r=i;break; } sort(v+1,v+1+r,cmp1); for(int i=1;i<=r;i++) if(v[i].h!=0){ l=i;break; } sort(v+l,v+1+r,cmp2); for(int i=1;i<=n;i++) sh+=s[v[i].id]; int len=sh.length(); for(int i=0;i<len;i++){ if(sh[i]=='s') sum++; else ans+=sum; } cout<<ans; } /* 20 h h s s h s s h h h s s s h s h s h h h 99 */
后来发现，其实自己给l和r加上一个边界条件就能AC了。我就是个zz......
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; string sh; int n,l=1,r=n,sum; long long ans; string s[100001]; struct nond{ int s,h,id; }v[100001]; int cmp(nond a,nond b){ return a.s>b.s; } int cmp1(nond a,nond b){ return a.h<b.h; } int cmp2(nond a,nond b){ double x=(a.s*1.0)/(a.h*1.0); double y=(b.s*1.0)/(b.h*1.0); return x>y; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ cin>>s[i];v[i].id=i; int len=s[i].length(); for(int j=0;j<len;j++){ if(s[i][j]=='s') v[i].s++; if(s[i][j]=='h') v[i].h++; } } sort(v+1,v+1+n,cmp); for(int i=n;i>=1;i--) if(v[i].s!=0){ r=i;break; } sort(v+1,v+1+r,cmp1); for(int i=1;i<=r;i++) if(v[i].h!=0){ l=i;break; } sort(v+l,v+1+r,cmp2); for(int i=1;i<=n;i++) sh+=s[v[i].id]; int len=sh.length(); for(int i=0;i<len;i++){ if(sh[i]=='s') sum++; else ans+=sum; } cout<<ans; } /* 20 h h s s h s s h h h s s s h s h s h h h 99 */
Imp is really pleased that you helped him. But it you solve the last problem, his gladness would raise even more.
Let's define 
for some set of integers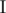 
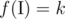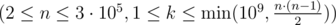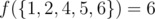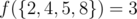as the number of pairs a, b in , such that:
- a is strictly less than b;
- a divides b without a remainder.
You are to find such a set , which is a subset of {1, 2, ..., n} (the set that contains all positive integers not greater than n), that 
.
The only line contains two integers n and k 
.
If there is no answer, print "No".
Otherwise, in the first line print "Yes", in the second — an integer m that denotes the size of the set you have found, in the second line print m integers — the elements of the set , in any order.
If there are multiple answers, print any of them.
Examples
input 3 3 output No
input 6 6 output Yes 5 1 2 4 5 6
input 8 3 output Yes 4 2 4 5 8
In the second sample, the valid pairs in the output set are (1, 2), (1, 4), (1, 5), (1, 6), (2, 4), (2, 6). Thus, 
.
In the third example, the valid pairs in the output set are (2, 4), (4, 8), (2, 8). Thus, 
.
题意：给定n和k，构造一个集合{1,2,3,...,n}的子集，使得在这个集合中恰好有kk对正整数(x,y), x<y满足x是y的约数。
暴力：
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,k; int num[100001]; void dfs(int tot,int pre){ if(tot>n||pre>n) return ; int sum=0; for(int i=1;i<=tot;i++) for(int j=i+1;j<=tot;j++) if(num[i]<num[j]&&num[j]%num[i]==0) sum++; if(sum==k){ cout<<"Yes"<<endl<<tot<<endl; for(int i=1;i<=tot;i++) cout<<num[i]<<" "; exit(0); } num[tot+1]=pre+1; dfs(tot+1,pre+1); dfs(tot,pre+1); } int main(){ scanf("%d%d",&n,&k); dfs(0,0); cout<<"No"; }
赶脚自己实在是做不出来了。。。
( ^_^ )/~~拜拜
去网上扒了一篇大佬的题解然而木有怎么看懂，就这样了吧。。。。。（=u=.......）
选定11和22， 首先把满足 x>[n2] x>[n2] 的质数xx留出来， 然后把满足 [n3] <x<=[n2] [n3] <x<=[n2] 的质数，以及他们的两倍留出来， 留出来的这些数先不选，从33开始一个个开始选。 接近kk的时候开始选刚刚留出来的那些数, 先选满足 x>[n2] x>[n2] 的质数，满足题意的正整数对数加11， 再选满足 [n3] <x<=[n2] [n3] <x<=[n2] 的质数的两倍，满足题意的正整数对数加22， 最后选满足 [n3] <x<=[n2] [n3] <x<=[n2] 的质数，满足题意的正整数对数加22。 选完这些如果还是到不了kk，那么无解。 本来想着nn小的时候直接特判（O(2n)O(2n)暴力）的，但是把特判去掉交上去居然也通过了……
#include <bits/stdc++.h> using namespace std; #define rep(i, a, b) for (int i(a); i <= (b); ++i) #define dec(i, a, b) for (int i(a); i >= (b); --i) const int N = 3e5 + 10; int a[N], b[N], c[N], f[N]; int n, k, num1 = 0, num2 = 0; vector <int> c1, c21, c22; vector <int> ans; void print(){ puts("Yes"); sort(ans.begin(), ans.end()); int sz = ans.size(); printf("%d\n", sz); int fg = 0; for (auto u : ans){ if (!fg) fg = 1; else putchar(32); printf("%d", u); } putchar(10); exit(0); } void calc(){ int x1 = c1.size(), x21 = c21.size(), x22 = c22.size(); if (k & 1){ if (num1 == 0){ puts("No"); exit(0);} while (k >= 3 && x22 > 0){ k -= 2; --x22; ans.push_back(c22[x22]); c22.pop_back(); } while (k >= 3 && x21 > 0){ k -= 2; --x21; ans.push_back(c21[x21]); c21.pop_back(); } while (k > 0 && x1 > 0){ k--; --x1; ans.push_back(c1[x1]); c1.pop_back(); } if (k > 0){ puts("No"); exit(0); } print(); } else{ while (k >= 2 && x22 > 0){ k -= 2; --x22; ans.push_back(c22[x22]); c22.pop_back(); } while (k >= 2 && x21 > 0){ k -= 2; --x21; ans.push_back(c21[x21]); c21.pop_back(); } while (k > 0 && x1 > 0){ k--; --x1; ans.push_back(c1[x1]); c1.pop_back(); } if (k > 0){ puts("No"); exit(0);} print(); } } int main(){ scanf("%d%d", &n, &k); rep(i, 2, 3e5 + 1){ if (!b[i]){ for (int j = i + i; j <= 3e5 + 1; j += i) b[j] = 1; } } rep(i, 1, 3e5 + 1){ for (int j = i; j <= 3e5 + 1; j += i) ++f[j]; --f[i]; } c[1] = 1, c[2] = 1; rep(i, n / 2 + 1, n) if (!b[i]){ if (i <= 2) continue; c[i] = 1; c1.push_back(i); ++num1; } rep(i, n / 3 + 1, n / 2) if (!b[i]){ if (i <= 2) continue; c[i] = 1; c[i << 1] = 1; c21.push_back(i); c22.push_back(i * 2); ++num2; } --k; ans.push_back(1); ans.push_back(2); if (k == 0) print(); rep(i, 3, n){ if (c[i]) continue; if (k >= f[i]){ k -= f[i]; ans.push_back(i); } else calc(); } calc(); return 0; }
然并卵，大佬可能不是用的c++，我竟然编译木有过，太尴尬了。。
