洛谷 P1187 3D模型

P1187 3D模型

题目描述

一座城市建立在规则的n×m网格上，并且网格均由1×1正方形构成。在每个网格上都可以有一个建筑，建筑由若干个1×1×1的立方体搭建而成（也就是所有建筑的底部都在同一平面上的）。几个典型的城市模型如下图所示：

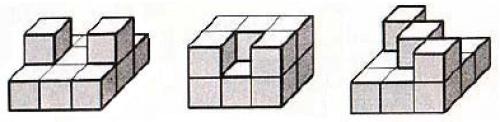
现在给出每个网格上建筑的高度，即每个网格上建筑由多少个立方体搭建而成，要求这个建筑模型的表面积是多少。

输入输出格式

输入格式：

 

输入文件的第1行包含2个正整数n和m，为城市模型的长与宽。

接下来n行，每行m个数字字符，描述了网格每个格子高度（可见所有建筑高度都大等于0且小等于9）。

 

输出格式：

 

输出文件包含一个非负整数，为城市模型的表面积。

 

输入输出样例

输入样例#1： 复制

3 3
111
212
111

输出样例#1： 复制

38

输入样例#2： 复制

3 4
1000
0010
0000

输出样例#2： 复制

12

说明

本题有2个测试数据

20%的数据满足：n, m≤10；

40%的数据满足：n, m≤100；

100%的数据满足：n, m≤1000。

思路：上正侧，一个判断一次即可，最后答案乘2，模拟。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,m,ans;
char s[1010];
int map[1010][1010];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%s",s);
        for(int j=0;j<m;j++)
            map[i][j+1]=s[j]-'0';
    }    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(map[i][j])    ans++;
    for(int j=1;j<=m;j++){
        ans+=map[1][j];
        for(int i=2;i<=n;i++)
            if(map[i][j]>map[i-1][j])
                ans+=map[i][j]-map[i-1][j];
    }
    for(int i=1;i<=n;i++){
        ans+=map[i][1];
        for(int j=2;j<=m;j++)
            if(map[i][j]>map[i][j-1])
                ans+=map[i][j]-map[i][j-1];
    }
    cout<<ans*2;
}