洛谷 P3382 【模板】三分法
题目描述
如题,给出一个N次函数,保证在范围[l,r]内存在一点x,使得[l,x]上单调增,[x,r]上单调减。试求出x的值。
输入输出格式
输入格式:
第一行一次包含一个正整数N和两个实数l、r,含义如题目描述所示。
第二行包含N+1个实数,从高到低依次表示该N次函数各项的系数。
输出格式:
输出为一行,包含一个实数,即为x的值。四舍五入保留5位小数。
输入输出样例
说明
时空限制:50ms,128M
数据规模:
对于100%的数据:7<=N<=13
样例说明:
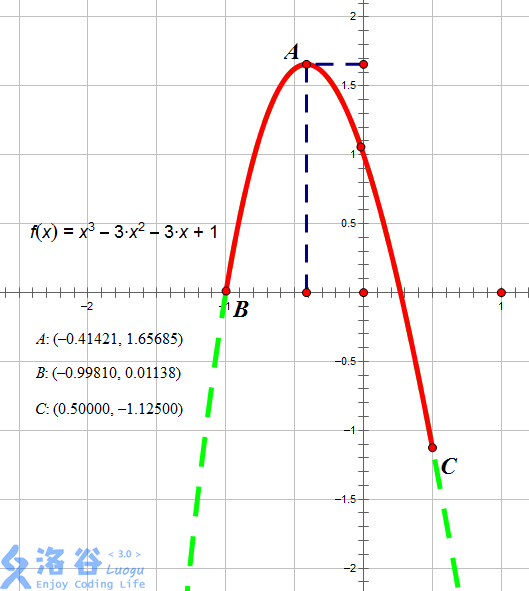
如图所示,红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。
当x=-0.41421时图像位于最高点,故此时函数在[l,x]上单调增,[x,r]上单调减,故x=-0.41421,输出-0.41421。
思路:三分法。
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define eps 1e-7 using namespace std; int n; double a[15]; double l,r,mid1,mid2; double f(double x){ double sum=0; for(int i=n;i>=0;i--) sum+=a[i]*pow(x,i); return sum; } int main(){ scanf("%d%lf%lf",&n,&l,&r); for(int i=n;i>=0;i--) scanf("%lf",&a[i]); while(r-l>eps){ mid1=(2*l+r)/3; mid2=(l+2*r)/3; if(f(mid1)<f(mid2)) l=mid1; else r=mid2; } printf("%.5lf",l); }
细雨斜风作晓寒。淡烟疏柳媚晴滩。入淮清洛渐漫漫。
雪沫乳花浮午盏,蓼茸蒿笋试春盘。人间有味是清欢。


