湖南测试 1

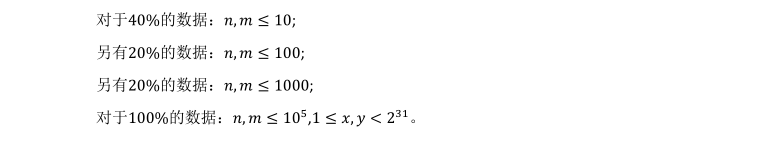
思路：二分答案水过

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100100
using namespace std;
int n,m,tx,ty,ans;
int cntx[MAXN],cnty[MAXN];
struct nond{
    int x,y,d;
    double k;
}cnt[MAXN];
bool check(int mid){
    double dy=cnt[mid].k*tx+cnt[mid].d;
    if(dy<=ty)    return true;
    else return false;
}
int main(){
    freopen("geometry.in","r",stdin);
    freopen("geometry.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&cntx[i]);
    for(int i=1;i<=n;i++)
        scanf("%d",&cnty[i]);
    sort(cntx+1,cntx+1+n);
    sort(cnty+1,cnty+1+n);
    for(int i=1;i<=n;i++){
        cnt[i].x=cntx[i];
        cnt[i].y=cnty[i];
        cnt[i].k=-1*(cnty[i]*1.0/cntx[i]*1.0);
        cnt[i].d=cnty[i];
    }
    scanf("%d",&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&tx,&ty);
        int l=0,r=n,mid;
        while(l<=r){
            mid=(l+r)/2;
            if(check(mid))    l=mid+1,ans=mid;
            else r=mid-1;
        }
        cout<<ans<<endl;
    }
}

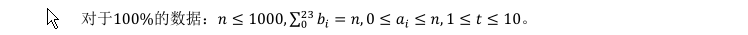
思路：贪心，水了45分，据说大佬的贪心可以水85分的。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 50
using namespace std;
int t,sum,ans;
int need[MAXN],people[MAXN],vis[MAXN];
int main(){
    freopen("cashier.in","r",stdin);
    freopen("cashier.out","w",stdout);
    scanf("%d",&t);
    while(t--){
        ans=0;
        bool flag=0;
        memset(vis,0,sizeof(vis));
        memset(need,0,sizeof(need));
        memset(people,0,sizeof(people));
        for(int i=1;i<=24;i++){ scanf("%d",&need[i]); need[24+i]=need[i]; }    
        for(int i=1;i<=24;i++){ scanf("%d",&people[i]); people[24+i]=people[i]; }    
        for(int i=25;i<=48;i++){
            if(need[i]!=0){
                sum=0;
                for(int j=i-7;j<=i;j++)
                    if(vis[j]!=0)    sum+=vis[j];
                if(sum>=need[i])    continue;
                if(i-7>=25){
                    for(int j=i;j>=i-7;j--)
                        if(vis[j]!=people[j]&&people[j]!=0){
                            if(sum==need[i])    break;
                            if(sum+people[j]-vis[j]<=need[i])    sum+=people[j]-vis[j],vis[j]=people[j];
                            else if(sum+people[j]-vis[j]>need[i])    vis[j]=need[i]-sum,sum=need[i];
                        }
                }
                else{
                    for(int j=i-7;j<=i;j++)
                        if(vis[j]!=people[j]&&people[j]!=0){
                            if(sum==need[i])    break;
                            if(sum+people[j]-vis[j]<=need[i]){
                                sum+=people[j]-vis[j],vis[j]=people[j];
                                if(j<=24)    sum+=people[j]-vis[j],vis[j+24]=people[j];    
                            }    
                            else if(sum+people[j]-vis[j]>need[i]){
                                vis[j]=need[i]-sum,sum=need[i];
                                if(j<=24)    vis[j+24]=need[i]-sum,sum=need[i];
                            }
                        }
                }
                if(sum<need[i]){ cout<<"-1";flag=1;break; }
            }
        }
        for(int i=25;i<=48;i++)    ans+=vis[i];
        if(!flag)    cout<<ans<<endl;
    }
}
/*
1
0 0 0 0 0 0 0 0 4 5 2 2 2 6 3 2 4 3 2 1 1 2 1 0
1 1 1 0 0 0 1 1 3 1 1 0 0 2 0 0 0 3 1 1 1 0 0 2
1
0 1 0 0 0 0 0 0 2 2 1 5 2 0 3 1 1 4 1 4 2 6 3 3
1 1 1 0 1 0 0 0 0 1 3 2 0 0 4 0 3 0 1 0 0 2 0 0
*/

正解思路：查分约束

记录前缀和sum[i](前缀和是指最终应该得到的答案的前缀和)

当i>=8时 应该满足条件：s[i]-s[i-8]>=a[i];

　　　　　　　　　　　　0<=s[i]-s[i-1]<=b[i];

当i<  8时 应该满足条件：s[23]-s[16+i]+s[i]>=a[i];（下标从0开始）

但是第3个式子并不满足差分约束的性质。

我们可以发现第三个式子中的s[23]具有单调性，所以可以从小到大枚举s[23]是几，第一个符合条件的一定是最小的（s[23](也就是最终的答案是几),二分s[23]的值也可以），然后就可以转为符合差分约束的式子：

　　s[i]-s[16+i]>=a[i]-s[23];

然后spfa判负环，跑差分约束即可。

#include<queue> 
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 50
using namespace std;
queue<int>que;
int t,tot,ans;
int a[MAXN],b[MAXN];
int dis[MAXN],vis[MAXN];
int to[MAXN*2],cap[MAXN*2],net[MAXN*2],head[MAXN*2];
void add(int u,int v,int w){
    to[++tot]=v;cap[tot]=w;net[tot]=head[u];head[u]=tot;
}
bool spfa(int s){
    memset(vis,0,sizeof(vis));
    memset(dis,-0x7f7f7f7f,sizeof(dis));
    while(!que.empty())    que.pop();
    que.push(s);
    dis[s]=0;vis[s]=1;
    while(!que.empty()){
        int now=que.front();
        que.pop();
        vis[now]=0;
        if(dis[now]>1000)    return false;
        for(int i=head[now];i;i=net[i])
            if(dis[to[i]]<dis[now]+cap[i]){
                dis[to[i]]=dis[now]+cap[i];
                if(!vis[to[i]]){
                    vis[to[i]]=1;
                    que.push(to[i]);
                }
            }
    }
    return true;
}
bool judge(int ans){
    memset(head,0,sizeof(head));tot=0;
    for(int i=9;i<=24;i++)    add(i-8,i,a[i]);
    for(int i=1;i<=8;i++)    add(i+16,i,a[i]-ans);
    for(int i=1;i<=24;i++)    add(i-1,i,0);
    for(int i=1;i<=24;i++)    add(i,i-1,-b[i]);
    add(0,24,ans);
    add(24,0,-ans);
    return spfa(0);
}
int main(){
    freopen("cashier.in","r",stdin);
    freopen("cashier.out","w",stdout);
    scanf("%d",&t);
    while(t--){
        for(int i=1;i<=24;i++)    scanf("%d",&a[i]);
        for(int i=1;i<=24;i++)    scanf("%d",&b[i]);
        ans=0;
        while(1){
            if(++ans>1000){
                ans=-1;
                break;
            }
            if(judge(ans))    break;
        }
        cout<<ans<<endl;
    }
}
/*
1
0 0 0 0 0 0 0 0 2 2 1 5 2 0 3 1 1 4 1 4 2 6 3 3
1 1 1 0 1 0 0 0 0 1 3 2 0 0 4 0 3 0 1 0 0 2 0 0
*/

 

 

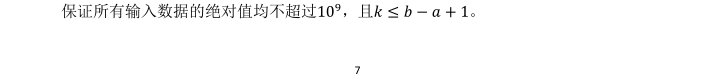
思路：

 自己写的80分暴力的线段树，然并卵，爆零了，QwQ求大佬找茬...

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN  50100
#define mod 1000000007
using namespace std;
int n,m;
struct nond{
    int l,r;
    long long sum;
    long long flag1,flag2;
}tree[MAXN*4];
void up(int now){
    tree[now].sum=(tree[now*2].sum+tree[now*2+1].sum)%mod;
}
void build(int now,int l,int r){
    tree[now].l=l;
    tree[now].r=r;
    tree[now].flag2=1;
    if(tree[now].l==tree[now].r){
        scanf("%d",&tree[now].sum);
        return ;
    }
    int mid=(tree[now].l+tree[now].r)/2;
    build(now*2,l,mid);
    build(now*2+1,mid+1,r);
    up(now);
}
void down(int now){
    tree[now*2].flag2=(tree[now].flag2*tree[now*2].flag2)%mod;
    tree[now*2+1].flag2=(tree[now].flag2*tree[now*2+1].flag2)%mod;
    tree[now*2].flag1=(tree[now].flag2*tree[now*2].flag1%mod+tree[now].flag1)%mod;
    tree[now*2+1].flag1=(tree[now].flag2*tree[now*2+1].flag1%mod+tree[now].flag1)%mod;
    tree[now*2].sum=(tree[now].flag2*tree[now*2].sum%mod+tree[now].flag1*(tree[now*2].r-tree[now*2].l+1)%mod)%mod;
    tree[now*2+1].sum=(tree[now].flag2*tree[now*2+1].sum%mod+tree[now].flag1*(tree[now*2+1].r-tree[now*2+1].l+1)%mod)%mod;
    tree[now].flag2=1;
    tree[now].flag1=0;
}
void change1(int now,int l,int r,int k){
    if(tree[now].l==l&&tree[now].r==r){
        tree[now].flag1+=k;
        tree[now].sum+=1ll*(tree[now].r-tree[now].l+1)*k;
        return ;
    }
    down(now);
    int mid=(tree[now].l+tree[now].r)/2;
    if(r<=mid)    change1(now*2,l,r,k);
    else if(l>mid)    change1(now*2+1,l,r,k);
    else{
        change1(now*2,l,mid,k);
        change1(now*2+1,mid+1,r,k);
    }
    up(now);
}
void change2(int now,int l,int r,int v){
    if(tree[now].l==l&&tree[now].r==r){
        tree[now].flag2=(tree[now].flag2*v)%mod;
        tree[now].flag1=(tree[now].flag1*v)%mod;
        tree[now].sum=(tree[now].sum*v)%mod;
        return ;
    }
    down(now);
    int mid=(tree[now].l+tree[now].r)/2;
    if(r<=mid)    change2(now*2,l,r,v);
    else if(l>mid)    change2(now*2+1,l,r,v);
    else{
        change2(now*2,l,mid,v);
        change2(now*2+1,mid+1,r,v);
    }
    up(now);
}
long long query(int now,int l,int r){
    if(tree[now].l==l&&tree[now].r==r)
        return tree[now].sum%mod;
    down(now);
    int mid=(tree[now].l+tree[now].r)/2;
    if(r<=mid)    return query(now*2,l,r);
    else if(l>mid)    return query(now*2+1,l,r);
    else return query(now*2,l,mid)+query(now*2+1,mid+1,r);
}
int main(){
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    scanf("%d%d",&n,&m);
    build(1,1,n);
    for(int i=1;i<=m;i++){
        int a,b,c,d;
        scanf("%d%d%d",&a,&b,&c);
        if(a==1){
            scanf("%d",&d);
            change1(1,b,c,d);
        }
        if(a==2)    change2(1,b,c,-1);
        if(a==3){
            scanf("%d",&d);
            if(d==1){
                long long ans=0;
                ans=query(1,b,c);
                if(ans<0)    ans+=mod;
                cout<<ans<<endl;
            }    
            if(d==2){
                long long ans=0;
                for(int i=b;i<c;i++)
                    ans=(ans+query(1,i+1,c)*query(1,i,i))%mod;
                if(ans<0)    ans+=mod;
                cout<<ans<<endl;
            }
        }
    }
}
/*
10 9
3 6 7 4 6 1 6 7 2 6
3 5 7 3
1 1 7 -9
1 2 3 5
3 2 6 1
2 5 8
3 5 7 3
2 2 3
3 1 10 2
3 1 2 2
*/

线段树

部分分可以dp f[i][j]表示前i个数选了j个的答案

f[i][j]=f[i-1][j]+f[i-1][j-1]*a[i] (i选不选)

k=1时线段树区间求和区间修改，我只会这个....

 

线段树区间合并操作。

k比较小，所以线段树每个节点维护一个区间答案记为f[i]

考虑一段区间i,左边取j个右边就取i-j个 答案是每个方案的左边乘右边的和。

就是i左儿子f[j]和右边的f[i-j] 所以f[i]=Σ(j=0~i) lc f[j]*rc f[i-j]

考虑取反操作，i是奇数就取反，偶数无影响(因为是相乘)

考虑区间加， 开始f[i] 是 a1*a2……an  后来是(a1+c)*(a2+c)……(an+c)

考虑类似二项式定理,当上述a1~an  n个方案如果取了j个了，分别为al1,al2……alj

那考虑最后答案，如果已经选了j个方案是(al1+c)(al2+c)……(alj+c)再还能选i-j个 最后答案是C(len-i,i-j)*f[j]*c^(i-j)

复杂度 O(k^2*nlogn)

 

只懂思路，代码....果断粘std

#include <cstdio>
#include <cstdlib>
#define MOD 1000000007
#define N 100005
typedef long long LL;
using namespace std;
struct Node
{
    LL f[11];
} node[N * 4];
LL a[N], lazy1[N * 4];
bool lazy2[N * 4];
LL C[N][11];
 
Node merge(Node lc, Node rc)
{
    Node o;
    o.f[0] = 1;
    for (int i = 1; i <= 10; i++)
    {
        o.f[i] = 0;
        for (int j = 0; j <= i; j++)
            o.f[i] = (o.f[i] + lc.f[j] * rc.f[i - j] % MOD) % MOD;
    }
    return o;
}
 
void build(int o, int l, int r)
{
    if (l == r)
    {
        for (int i = 0; i <= 10; i++) node[o].f[i] = 0;
        node[o].f[0] = 1;
        node[o].f[1] = (a[l] % MOD + MOD) % MOD;
        return ;
    }
    int mid = (l + r) >> 1;
    build(o * 2, l, mid);
    build(o * 2 + 1, mid + 1, r);
    node[o] = merge(node[o * 2], node[o * 2 + 1]);
    return ;
}
 
void update1(int o, int l, int r, int c)
{
    int len = r - l + 1;
    LL ff[11];
    for (int i = 0; i <= 10; i++) ff[i] = node[o].f[i];
    for (int i = 1; i <= 10; i++)
    {
        node[o].f[i] = 0;
        LL t = 1;
        for (int j = 0; j <= i; j++)
        {
            LL tmp = ff[i - j] * C[len - (i - j)][j] % MOD * t % MOD;
            node[o].f[i] = (node[o].f[i] + tmp) % MOD;
            t = t * c % MOD;
        }
    }
    return ;
}
 
void push_down(int o, int l, int r)
{
    int mid = (l + r) >> 1;
    if (lazy1[o])
    {
        if (lazy2[o * 2])
            lazy1[o * 2] = (lazy1[o * 2] + MOD - lazy1[o]) % MOD;
        else
            lazy1[o * 2] = (lazy1[o * 2] + lazy1[o]) % MOD;
        if (lazy2[o * 2 + 1])
            lazy1[o * 2 + 1] = (lazy1[o * 2 + 1] + MOD - lazy1[o]) % MOD;
        else
            lazy1[o * 2 + 1] = (lazy1[o * 2 + 1] + lazy1[o]) % MOD;
        update1(o * 2, l, mid, lazy1[o]);
        update1(o * 2 + 1, mid + 1, r, lazy1[o]);
        lazy1[o] = 0;
    }
    if (lazy2[o])
    {
        lazy2[o * 2] ^= 1;
        lazy2[o * 2 + 1] ^= 1;
        for (int j = 1; j <= 10; j += 2)
        {
            node[o * 2].f[j] = MOD - node[o * 2].f[j];
            node[o * 2 + 1].f[j] = MOD - node[o * 2 + 1].f[j];
        }
        lazy2[o] = 0;
    }
}
 
void modify1(int o, int l, int r, int ll, int rr, int c)
{
    if (ll <= l && rr >= r)
    {
        if (lazy2[o]) lazy1[o] = (lazy1[o] + MOD - c) % MOD;
        else lazy1[o] = (lazy1[o] + c) % MOD;
        update1(o, l, r, c);
        return ;
    }
    int mid = (l + r) >> 1;
    push_down(o, l, r);
    if (ll <= mid) modify1(o * 2, l, mid, ll, rr, c);
    if (rr > mid) modify1(o * 2 + 1, mid + 1, r, ll, rr, c);
    node[o] = merge(node[o * 2], node[o * 2 + 1]);
    return ;
}
 
void modify2(int o, int l, int r, int ll, int rr)
{
    if (ll <= l && rr >= r)
    {
        for (int i = 1; i <= 10; i += 2) node[o].f[i] = MOD - node[o].f[i];
        lazy2[o] ^= 1;
        return ;
    }
    int mid = (l + r) >> 1;
    push_down(o, l, r);
    if (ll <= mid) modify2(o * 2, l, mid, ll, rr);
    if (rr > mid) modify2(o * 2 + 1, mid + 1, r, ll, rr);
    node[o] = merge(node[o * 2], node[o * 2 + 1]);
    return ;
}
 
Node query(int o, int l, int r, int ll, int rr)
{
    if (ll <= l && rr >= r)
        return node[o];
    int mid = (l + r) >> 1;
    push_down(o, l, r);
    if (rr <= mid) return query(o * 2, l, mid, ll, rr);
    if (ll > mid) return query(o * 2 + 1, mid + 1, r, ll, rr);
    Node lc = query(o * 2, l, mid, ll, rr);
    Node rc = query(o * 2 + 1, mid + 1, r, ll, rr);
    return merge(lc, rc);
}
 
int main(int argc, char ** argv)
{
    freopen("game.in", "r", stdin);
    freopen("game.out", "w", stdout);
    int n, m;
    scanf("%d %d", &n, &m);
    C[0][0] = 1;
    for (int i = 1; i <= n; i++)
    {
        C[i][0] = 1;
        for (int j = 1; j <= 10; j++)
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
    }
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    for (int i = 1; i <= m; i++)
    {
 
        int l, r, opt;
        scanf("%d%d%d",&opt, &l, &r);
        if (opt == 1)
        {
            int c;
            scanf("%d", &c);
            c = (c % MOD + MOD) % MOD;
            modify1(1, 1, n, l, r, c);
        }
        else if (opt == 2)
        {
            modify2(1, 1, n, l, r);
        }
        else
        {
            int k;
            scanf("%d", &k);
            Node o = query(1, 1, n, l, r);
            printf("%d\n", o.f[k] % MOD);
        }
    }
    return 0;
}