bzoj 4806: 炮

4806: 炮

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 663  Solved: 320
[Submit][Status][Discuss]

Description

众所周知，双炮叠叠将是中国象棋中很厉害的一招必杀技。炮吃子时必须隔一个棋子跳吃，即俗称"炮打隔子"。 

炮跟炮显然不能在一起打起来，于是rly一天借来了许多许多的炮在棋盘上摆了起来……他想知道，在N×M的矩形

方格中摆若干炮（可以不摆）使其互不吃到的情况下方案数有几种。

棋子都是相同的。

 

Input

一行，两个正整数N和M。

N<=100,M<=100

 

Output

一行，输出方案数mod 999983。

 

Sample Input

1 3

Sample Output

7

HINT

 

Source

By FancyCoder

思路：f[i][j][k]表示截止到第i行为止，在所有的列中有一个炮的有j列，有2个炮的有k列。

举一个例子：

 

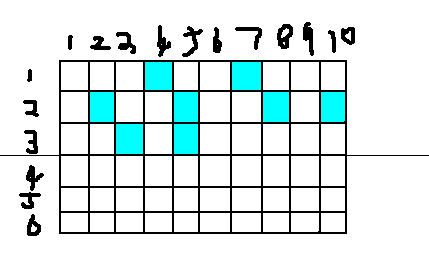
比如，这个图假设是截止到第3行为止，就可以表示成f[3][6][1]。

然后，我们就可以推想出以下6种状态：

1：在下一行什么也不放：　f[i+1][j][k]=f[i+1][j][k]+f[i][j][k];

2：在下一行中找一个0个炮的列去放一个炮：　　f[i+1][j+1][k]=f[i+1][j+1][k]+f[i][j][k]*(m-j-k);

3：在下一行中找一个1个炮的列去放一个炮：　　f[i+1][j-1][k+1]=f[i+1][j-1][k+1]+f[i][j][k]*j;

4：在下一行中找两个0个炮的列去分别放一个炮：　　f[i+1][j+2][k]=f[i+1][j+2][k]+f[i][j][k]*(m-j-k)*(m-j-k-1)/2;

（这里运用了组合数公式，因为有m-j-k个0个炮的列，任选两个进行组合，一共有C²_m-j-k种放法，化简开来就是有(m-j-k)*(m-j-k-1)/2种）

5：在下一行中找一个0个炮的列和一个1个炮的列分别去放一个炮：　　f[i+1][j][k+1]=f[i+1][j][k+1]+f[i][j][k]*(m-j-k)*j;

6：在下一行中找两个1个炮的列去分别放一个炮：　　f[i+1][j-2][k+2]=f[i+1][j-2][k+2]+f[i][j][k]*j*(j-1)/2;

最后的ans是所有的f[n]加起来：　　ans=ans+f[n][j][k];

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 999983
#define MAXN 110
using namespace std; 
int n,m,i,j,k; 
long long f[MAXN][MAXN][MAXN];
int main(){
    //freopen("B.in","r",stdin);
    //freopen("B.out","w",stdout);
    scanf("%d%d",&n,&m); 
    f[0][0][0]=1; 
    for(int i=0;i<=n-1;i++) 
        for(int j=0;j<=m;j++)
            for(int k=0;k<=m-j;k++)
                if(f[i][j][k]){ 
                    f[i+1][j][k]=(f[i+1][j][k]+f[i][j][k])%mod; 
                    f[i+1][j+1][k]=(f[i+1][j+1][k]+f[i][j][k]*(m-j-k))%mod; 
                    if(j>=1)    f[i+1][j-1][k+1]=(f[i+1][j-1][k+1]+f[i][j][k]*j)%mod;   
                    if(m-j-k>=2)    f[i+1][j+2][k]=(f[i+1][j+2][k]+f[i][j][k]*((m-j-k)*(m-j-k-1)/2))%mod; 
                    if(j>=1&&m-j-k>=1)    f[i+1][j][k+1]=(f[i+1][j][k+1]+f[i][j][k]*(j*(m-j-k)))%mod; 
                    if(j>=2)    f[i+1][j-2][k+2]=(f[i+1][j-2][k+2]+f[i][j][k]*(j*(j-1)/2))%mod; 
                } 
    long long ans=0; 
    for(int j=0;j<=m;j++)
        for(int k=0;k<=m-j;k++)
            ans=(ans+f[n][j][k])%mod; 
    cout<<ans; 
}