算法可视化

  • 本代码参考慕课网的liuyubobobo老师的一门课《7个经典应用诠释Java算法精髓》，并且基于课程中的参考代码做了一定的完善和个人定制。
  • 以Java语言主讲，通过7款经典好玩游戏，真正将算法用于实际开发。

可视化用到的语言和技术

Java Swing

可视化内容

1. 概率模拟算法

使用蒙特卡洛算法模拟计算PI

2. 排序算法

选择排序可视化

插入排序可视化

归并排序可视化

3. 迷宫自动求解迷宫

  • 注：迷宫自动求解游戏添加了键盘点击事件按对应的键盘按键将触发相应的操作

    • 按数字1：深度优先遍历算法生成迷宫
    • 按数字2：深度优先遍历非递归算法生成迷宫
    • 按数字3：广度优先遍历算法生成迷宫
    • 按数字4：随机队列遍历算法生成迷宫
    • 按数字5：增强随机队列算法生成迷宫
    • 按数字7：深度优先遍历递归算法求解迷宫
    • 按数字8：深度优先遍历非递归算法求解迷宫
    • 按数字9：广度优先遍历算法求解迷宫
    • 按数字0：清屏，游戏回到迷雾笼罩的状态

  • 从文件中读取迷宫信息，并且进行可视化；

深度优先遍历递归写法+回溯法求解迷宫可视化；

深度优先遍历的非递归写法求解迷宫可视化；

广度优先遍历算法求解迷宫可视化；

4. 生成迷宫

  • 为了简单起见，在M行N列的迷宫中，先规定迷宫的入口是(1, 0)，出口是(M-2, N-1)

迷宫生成前的准备工作

下面是61x91规格的迷宫，奇数行和奇数列相交的位置是通路（没有墙），生成迷宫前需要先产生一个这样的图。然后只需要深度优先遍历所有在奇数行和奇数列相交的路，然后打破两个路之前的墙即可产生一个迷宫。

image-20210326235007632

深度优先遍历递归算法生成一个迷宫

深度优先遍历非递归算法生成一个迷宫

广度优先遍历非递归算法生成一个迷宫

创建一个随机队列让迷宫的生成过程更随机

给未生成部分添加迷雾，让生成迷宫的过程更具备观赏性和神秘感

随机队列的代码请参考RandomQueue.java

随机迷宫的生成过程如下图所示：

随机迷宫的求解过程如下图所示：

增强生成迷宫的随机性

经过多次迷宫的生成和求解过程来看，迷宫的解路径大致趋势是从左上到右下的一条不是很曲折的曲线，随机性还不够强，所以优化了随机队列的随机存取元素的代码，参考EnhancedRandomQueue.java

增强随机性后迷宫的生成过程如下图所示：

增强随机性后迷宫的求解过程如下图所示：

5. 扫雷

扫雷游戏胜利与游戏结束

游戏结束

注：游戏结束后可按回车重新开局！

image-20210328180303684

胜利

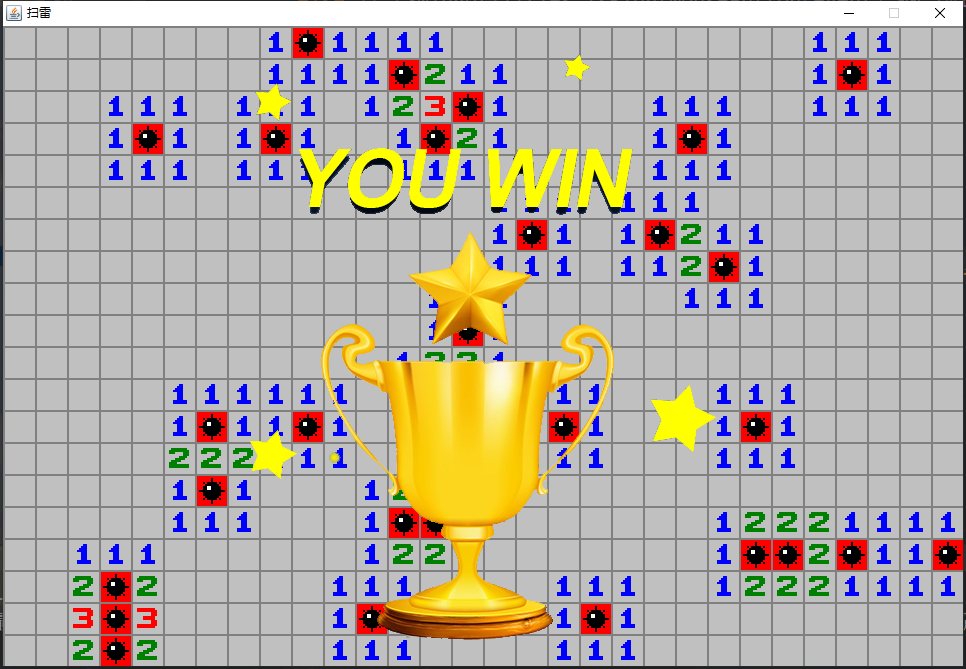
image-20210328212853457

在游戏盘面中随机30枚雷

image-20210328141001452

随机算法好坏评估

  • 算法目标：将指定数量的雷随机放在游戏区域中的相同数量的格子中

  • 使用大量次数统计的方法对三种随机打乱算法，参考RandomAlgorithmAssessment.java

    • arr：待随机打算顺序的数组；mineNumber：雷的个数（小于数组长度）

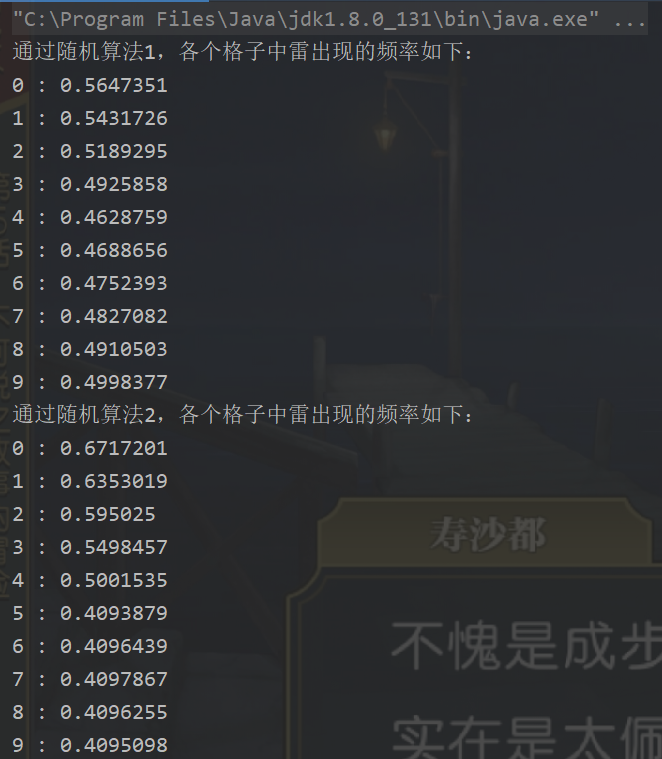
    • 随机算法1：将每一个格子上的值和随机的格子上的值进行交换

      for (int i = 0; i < arr.length; i++) {
    int j = (int) (Math.random() * arr.length);
    swap(arr, i, j);
}

    • 随机算法2：将每一个雷所在的格子上的值和随机的格子上的值进行交换

      for (int i = 0; i < mineNumber; i++) {
    int j = (int) (Math.random() * arr.length);
    swap(arr, i, j);
}

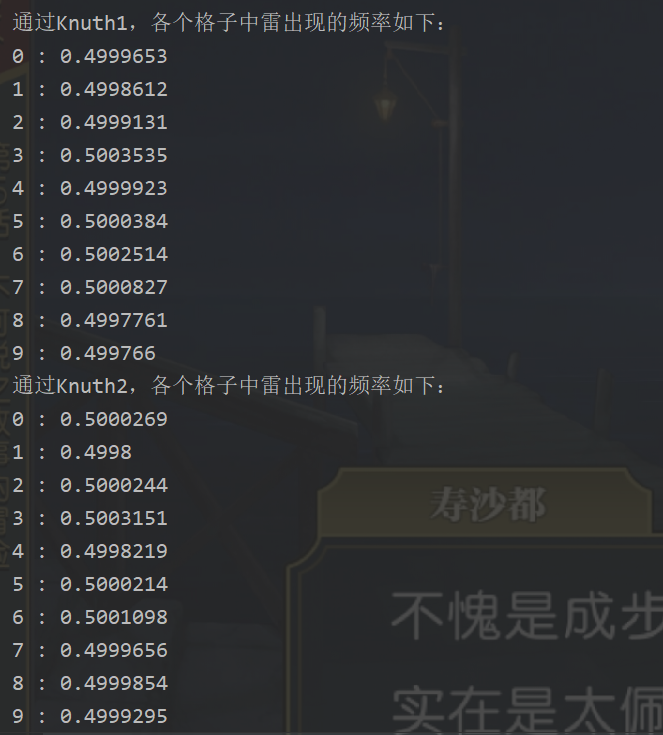
    • knuth算法：从[i, n)区间中随机获取元素，然后和第i个元素交换

      for (int i = 0; i < arr.length; i++) {
    int j = (int) (Math.random() * (arr.length - i) + i);
    swap(arr, i, j);
}

    • knuth算法的另一种写法，从[0, i+1)区间中随机获取元素，然后和第i个元素交换

      for (int i = arr.length - 1; i >= 0; i--) {
    int j = (int) (Math.random() * (i + 1));
    swap(arr, i, j);
}

    • 各个算法在N=10000000，n=10，m=5的情况下（N为统计次数，n为数组长度，m为数组中的雷的个数），数组中的各个位置上出现雷的频率如下图所示：

      image-20210328160137277

      image-20210328155957042

6. 移动箱子游戏给出求解步骤

游戏介绍：

这是一个三消类推箱子游戏，跟传统的推箱子不一样，这个推箱子需要你在规定的步数内移动箱子，促使游戏面板中三个相同的箱子连成一行或者一列，可以达成消除的条件，另外游戏设置了重力系统，高出的箱子如果往左或者往右或者它下面的箱子被消除了，都会促使这个箱子向下坠落，坠落以后，又会检测是否出现新的可消除的连续的三个相连的箱子，游戏封面如下

image-20210329180005073

这是游戏中的某一个关卡：要求在移动一步的条件下消除所有的箱子。

image-20210329180302902

游戏物体符号化

现将上面关卡中的箱子的分布转换为一个二维字符数组，连同操作步数一起保存到文件中。

1
.....
..A..
..B..
..A..
..B..
.BAB.
.BAB.
.ABA.

然后通过代码来读取操作步数和二维字符数组，为了对齐每列的字符，空的位置用 点 表示，不同种类的箱子用不同的字母表示。

渲染符号化的游戏物体

用代码读取后渲染到页面上如下图所示，由于没有原游戏的箱子素材，我就在网上找了一些图片进行了替换。

image-20210329182751415

查看求解步骤

为了使得求解后的答案更直观，在每一个箱子中间写了一个坐标，代表目前这个箱子所在的行和列。

image-20210329181210898

根据控制台打印出的结果和图上的坐标，去游戏里面进行相应操作即可通过此关。

交换 (3, 2) 和 (4, 2)
游戏有解！

7. 绘制分形图

递归绘制同心圆

image-20210329193958960

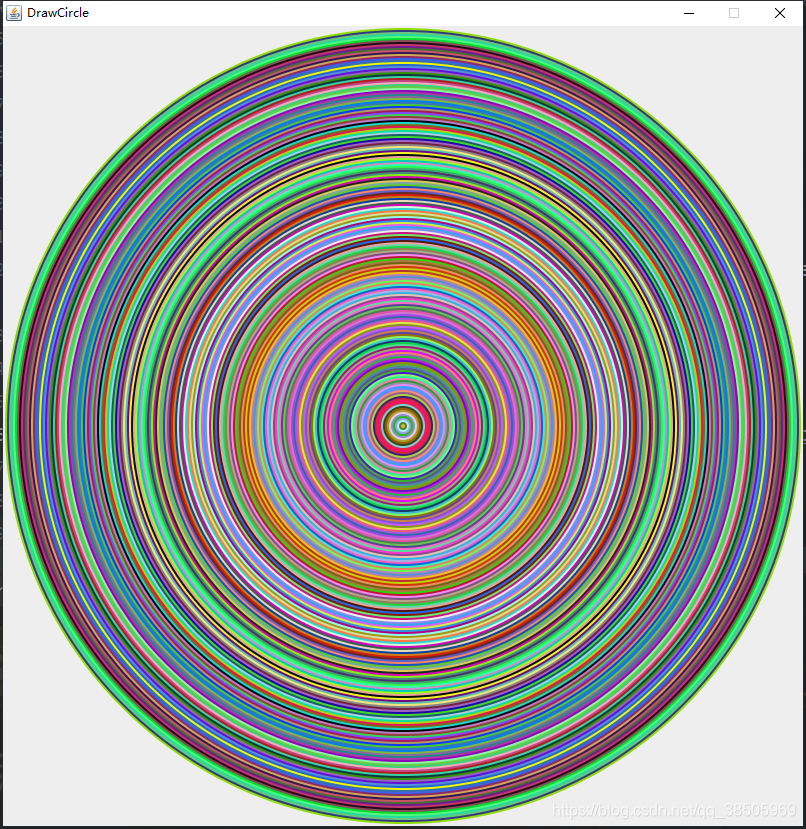
在这里插入图片描述

递归绘制vicsek（矩形）分形图

可以按键盘上的0到6进行不同递归次数的分形

初始化默认递归次数为0，呈现出整个区域都是一个颜色

分别按下键盘1-6又可以绘制出如下分形图

递归绘制SierpinskiCarpet（矩形）分形图

递归绘制SierpinskiTriangle（三角形）分形图

递归绘制KochSnowflake（雪花）分形图

递归绘制二叉树分形图