HDU 3944 DP? [Lucas定理 诡异的预处理]

DP?

Time Limit: 10000/3000 MS (Java/Others)    Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 3126    Accepted Submission(s): 978

Problem Description

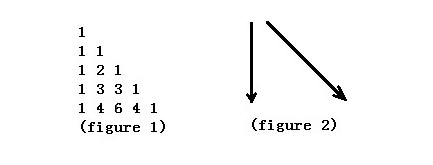
Input

Input to the problem will consists of series of up to 100000 data sets. For each data there is a line contains three integers n, k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is terminated by end-of-file.

 

---

数据范围诡异系列~

题意：杨辉三角可以往左或者往右走走到$(n,k)$的最小权值和

---

显然每一层都要取一个权值，并且越往外权值越小，当然是尽量往外最好啦

对称，k>n/2时变成n-k

如果从$(n,k)$向左斜着上去，结果就是

${n\choose k}+{n-1\choose k-1}+...+{n-k\choose 0}+n-k$

然后用组合数递推式合并，就是

${n+1\choose k}+n-k$

 

问题在于T太大啦，以致于<10000的质数远比T小，我们预处理模所有质数意义下的阶乘吧！

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=10007;
int n,m,P;
bool notp[N];
int p[N];
void sieve(int n){
    for(int i=2;i<=n;i++){
        if(!notp[i]) p[++p[0]]=i;
        for(int j=1;j<=p[0]&&i*p[j]<=n;j++){
            notp[i*p[j]]=1;
            if(i%p[j]==0) break;
        }
    }
}
int fac[N][1300],mp[N],pnum;
void ini(int n){
    sieve(n);
    for(int j=1;j<=p[0];j++){
        int x=p[j];mp[x]=j;
        fac[0][j]=1;
        for(int i=1;i<=n;i++) fac[i][j]=fac[i-1][j]*i%x;
    }
}
int Pow(int a,int b){
    int re=1;
    for(;b;b>>=1,a=a*a%P)
        if(b&1) re=re*a%P;
    return re;
}
int Inv(int a){return Pow(a,P-2);}
int C(int n,int m){
    if(n<m) return 0;
    return fac[n][pnum]*Inv(fac[m][pnum])%P*Inv(fac[n-m][pnum])%P;
}
int Lucas(int n,int m){
    if(n<m) return 0;
    int re=1;
    for(;m;n/=P,m/=P) re=re*C(n%P,m%P)%P;
    return re;
}
int main(){
    freopen("in","r",stdin);
    int cas=0;
    ini(10000);
    while(scanf("%d%d%d",&n,&m,&P)!=EOF){
        if(m>n/2) m=n-m;
        pnum=mp[P];
        printf("Case #%d: %d\n",++cas,(Lucas(n+1,m)+n-m)%P);
    }
}