HDU 1724 Ellipse [辛普森积分]

Ellipse

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1868    Accepted Submission(s): 792

Problem Description

Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..
Look this sample picture:



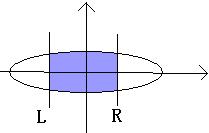
A ellipses in the plane and center in point O. the L,R lines will be vertical through the X-axis. The problem is calculating the blue intersection area. But calculating the intersection area is dull, so I have turn to you, a talent of programmer. Your task is tell me the result of calculations.(defined PI=3.14159265 , The area of an ellipse A=PI*a*b )

Input

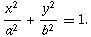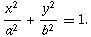Input may contain multiple test cases. The first line is a positive integer N, denoting the number of test cases below. One case One line. The line will consist of a pair of integers a and b, denoting the ellipse equation , A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).

 

Output

For each case, output one line containing a float, the area of the intersection, accurate to three decimals after the decimal point.

Sample Input

2 2 1 -2 2 2 1 0 2

 

Sample Output

6.283 3.142

---

可以计算椭圆面积了哈哈

注意eps小一点

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const double eps=1e-10;

double a,b,l,r;
inline double F(double x){
    return sqrt((a*a-x*x)/(a*a))*b;
}
inline double cal(double l,double r){
    return (F(l)+F(r)+4*F((l+r)/2))*(r-l)/6;
}
double Simpson(double l,double r,double now){
    double mid=(l+r)/2,p=cal(l,mid),q=cal(mid,r);
    if(abs(now-p-q)<eps) return now;
    else return Simpson(l,mid,p)+Simpson(mid,r,q);
}

int main(int argc, const char * argv[]) {
    int T;scanf("%d",&T);
    while(T--){
        scanf("%lf%lf%lf%lf",&a,&b,&l,&r);
        l=max(l,-a);r=min(r,a);
        printf("%.3f\n",2*Simpson(l,r,cal(l,r)));
    }

    return 0;
}