BZOJ 2154: Crash的数字表格 [莫比乌斯反演]

2154: Crash的数字表格

Time Limit: 20 Sec  Memory Limit: 259 MB
Submit: 2924  Solved: 1091
[Submit][Status][Discuss]

Description

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

Input

输入的第一行包含两个正整数，分别表示N和M。

Output

输出一个正整数，表示表格中所有数的和mod 20101009的值。

Sample Input

4 5

Sample Output

122
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。

---

计算所有lcm(i,j)的和

 

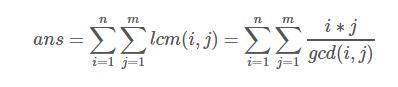
考虑每个gcd的取值，

 

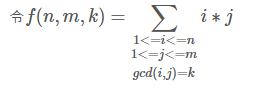
那么可以得到

ans=Σ{d=1...min(n,m)}f(n,m,d)/d 进一步改写方便分块

 

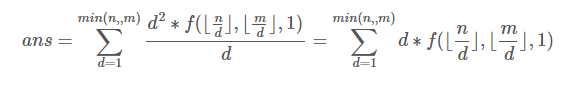
(原因：考虑所有gcd(i,j)=k的i和j都是ii*k和jj*k且gcd(ii,jj)=1)

 

问题就是求解f函数，发现f函数和bzoj2301中用的“

• f(i)为1<=x<=n,1<=y<=m且gcd(x,y)=i的数对(x,y)的个数

”很像，这个不是个数而是i*j的和，同样考虑莫比乌斯反演

构造F(x,y,k)为k|gcd(i,j)的i*j和，想办法直接算出F

 

 

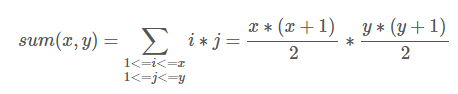
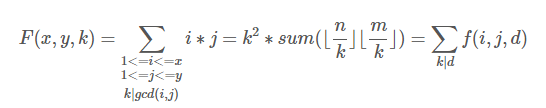
(原因：k|gcd(i,j) --> 所有的k的倍数)

 

莫比乌斯反演

 

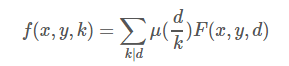
ans需要的部分即为

 

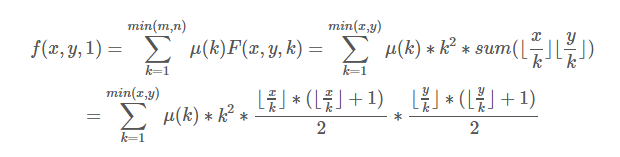
我们发现ans的部分用f可以sqrt(n)分块，求f的时候又可以sqrt(n)分块(处理mu[i]*i*i前缀和)，总共O(n)

 

 

经验：

需要f(x,y,1)想的时候不要只想1，这样并不好就行莫比乌斯反演

 

注意：

前缀和要用ll，然而本题int也没问题

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=1e7+5,MOD=20101009;
inline int read() {
    char c=getchar();
    int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int n,m;
bool notp[N];int p[N];
ll s[N],mu[N];
void sieve(int n){
    mu[1]=1;
    for(int i=2;i<=n;i++){
        if(!notp[i]) p[++p[0]]=i,mu[i]=-1;
        for(int j=1;j<=p[0]&&i*p[j]<=n;j++){
            int t=i*p[j];
            notp[t]=1;
            if(i%p[j]==0){
                mu[t]=0;
                break;
            }
            mu[t]=-mu[i];
        }
    }
    for(ll i=1;i<=n;i++)
     s[i]=(s[i-1]+(i*i*mu[i])%MOD)%MOD;
}
inline ll S(ll x,ll y){
    return ((x*(x+1)/2)%MOD)*((y*(y+1)/2)%MOD)%MOD;
}
ll f(ll n,ll m){
    ll ans=0,r=0;
    for(ll d=1;d<=n;d=r+1){
        r=min(n/(n/d),m/(m/d));
        ans=(ans+(s[r]-s[d-1])*S(n/d,m/d)%MOD)%MOD;
    }
    return ans;
}
int main() {
    n=read();
    m=read();
    sieve(n);
    if(n>m) swap(n,m);
    ll ans=0,r=0;
    for(ll d=1;d<=n;d=r+1){
        r=min(n/(n/d),m/(m/d));
        ans=(ans+f(n/d,m/d)*((r-d+1)*(r+d)/2)%MOD)%MOD;
    }
    printf("%lld",(ans+MOD)%MOD);

}