HDU1890 Robotic Sort[splay 序列]

Robotic Sort

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3913    Accepted Submission(s): 1717

Problem Description

Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes. 

In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order. 

Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B. 

A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc. 



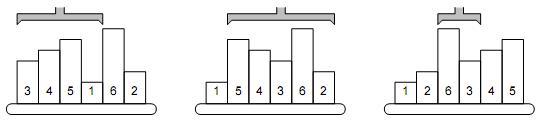
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc. 

Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too. 

 

 

Input

The input consists of several scenarios. Each scenario is described by two lines. The first line contains one integer number N , the number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N space-separated positive integers, they specify the heights of individual samples and their initial order. 

The last scenario is followed by a line containing zero. 

 

 

Output

For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation. 

Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed. 

 

 

Sample Input

6 3 4 5 1 6 2 4 3 3 2 1 0

 

 

Sample Output

4 6 4 5 6 6 4 2 4 4

---

题意：n个试管，每次找最短的位置p[i]输出，翻转i~p[i]

---

没想到写了好长时间

对序列的理解：

1.build之后数组下标就是序列编号，中序遍历就是序列

2.这样的splay并没有左小右大的关系，因为有反转操作

3.加哨兵之后，翻转序列[l,r]，就是处理kth(l)和kth(r+2)

 

一开始想了很多应该处理哪个序列，都错了

其实题目已经很清楚了，就是翻转i~p[i]

处理第i短的编号为x，x就是序列编号就是数组下标，把x splay到根然后p[i]=左子树大小+1(就是t[lc].size 因为1是哨兵)

翻转操作就是rever(i,t[lc].size);

 

关于标记下传：

1.翻转操作先要kth，在kth中下传了就没必要在splay中下传了

2.否则的话先从x找到tar，然后从tar往x下传标记，最后splay(x,tar)

 

//
//  main.cpp
//  hdu1890
//
//  Created by Candy on 30/11/2016.
//  Copyright © 2016 Candy. All rights reserved.
//
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define pa t[x].fa
#define lc t[x].ch[0]
#define rc t[x].ch[1]
const int N=1e5+5;
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
struct node{
    int fa,ch[2],w,size,flp;
}t[N];
int root;
inline void update(int x){t[x].size=t[lc].size+t[rc].size+t[x].w;}
inline int wh(int x){return t[pa].ch[1]==x;}
inline void pushDown(int x){
    if(t[x].flp){
        swap(lc,rc);
        t[lc].flp^=1;t[rc].flp^=1;
        t[x].flp=0;
    }
}
inline void rotate(int x){
    int f=t[x].fa,g=t[f].fa,c=wh(x);
    if(g) t[g].ch[wh(f)]=x;t[x].fa=g;
    t[f].ch[c]=t[x].ch[c^1];t[t[f].ch[c]].fa=f;
    t[x].ch[c^1]=f;t[f].fa=x;
    update(f);update(x);
}
inline void splay(int x,int tar){
    for(;t[x].fa!=tar;rotate(x))
        if(t[pa].fa!=tar) rotate(wh(pa)==wh(x)?pa:x);
    if(tar==0) root=x;
}
int ne[N];
void spl(int x,int tar){
    int _=x;
    while(x!=tar) ne[pa]=x,x=pa;
    x=_;
    for(int i=tar;i!=x;i=ne[i]) pushDown(i);
    pushDown(x);
    splay(x,tar);
}
int build(int l,int r){
    if(l>r) return 0;
    int x=(l+r)>>1;
    lc=build(l,x-1);rc=build(x+1,r);
    t[lc].fa=t[rc].fa=x;
    t[x].w=1;t[x].flp=0;
    update(x);
    //printf("build %d %d %d\n",x,lc,rc);
    return x;
}
int kth(int k){
    int x=root,ls=0;
    while(x!=0){
        pushDown(x);
        int _=ls+t[lc].size;
        if(_<k&&k<=_+t[x].w) return x;
        if(k<=_) x=lc;
        else ls=_+t[x].w,x=rc;
    }
    return -1;
}
void rever(int l,int r){//printf("rev %d %d ",l,r);
    splay(kth(l),0);
    int x=kth(r+2);//printf("x %d\n",x);
    splay(x,root);
    t[lc].flp^=1;
}
int n;
struct data{
    int id,v;
    bool operator <(const data &a)const{
        if(v==a.v) return id<a.id;
        return v<a.v;
    }
}a[N];
int main(int argc, const char * argv[]){
    while(scanf("%d",&n)!=EOF&&n){
        memset(t,0,sizeof(t));
        for(int i=1;i<=n;i++) a[i].v=read(),a[i].id=i+1;
        sort(a+1,a+1+n);
        root=build(1,n+2);
        for(int i=1;i<=n;i++){
            int x=a[i].id;//printf("hi %d %d\n",i,x);
            spl(x,0);
            printf("%d%c",t[lc].size,i<n?' ':'\n');
            rever(i,t[lc].size);
        }
    }
    return 0;
}