NOIP2003pj栈[卡特兰数]
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即pop(从栈顶弹出一个元素)和push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
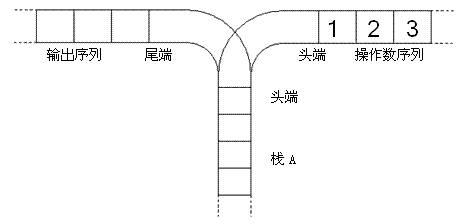
宁宁考虑的是这样一个问题:一个操作数序列,从1,2,一直到n(图示为1到3的情况),栈A的深度大于n。
现在可以进行两种操作,
1.将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的push操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的pop操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由1 2 3生成序列2 3 1的过程。
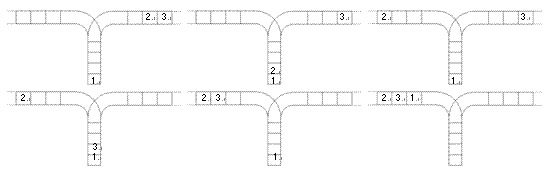
(原始状态如上图所示)
你的程序将对给定的n,计算并输出由操作数序列1,2,…,n经过操作可能得到的输出序列的总数。
输入输出格式
输入格式:
输入文件只含一个整数n(1≤n≤18)
输出格式:
输出文件只有一行,即可能输出序列的总数目
输入输出样例
输入样例#1:
3
输出样例#1:
5
按最后一个数分类,卡特兰数
一些知识:
令h(0)=1,h(1)=1,catalan数满足递推式
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
h(n)=h(n-1)*(4*n-2)/(n+1);
#include <cstdio> int main(){ long long n,f=1; scanf("%lld",&n); for(int i=1;i<=n;i++) f=f*(4*i-2)/(i+1); printf("%lld",f); }
Copyright:http://www.cnblogs.com/candy99/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号