Java集合之TreeMap源码解析中篇
前言
上期我介绍了TreeMap的基本结构以及put方法的解读，包括自平衡保持红黑树特性的种种变化，
从代码角度来看，红黑树是否需要自我调整必须满足三个条件，
1.当前结点不是空结点，
2.当前结点不是根节点，
3.当前结点的父结点必须为红色。
本期主要是承接上期Java集合之TreeMap源码解析上篇（←戳）的内容，继续深入探讨。
建立一个简单的红黑树
1 public static void main(String[] args) { 2 TreeMap<Integer, Integer> map = new TreeMap<Integer, Integer>(); 3 map.put(50,3001); 4 map.put(30,3002); 5 map.put(70,3003); 6 map.put(20,3004); 7 map.put(40,3005); 8 map.put(60,3006); 9 map.put(80,3007); 10 map.put(85,3008); 11 }
第2行，新增一个结点50，
由于root为null，因此50便成为树结构的根，颜色为黑色，如下图所示，
第3行，新增一个结点30，找到30的父结点为50，新增之后如下图所示
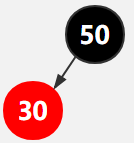
符合红黑树的5条规则，因此无须调整，
第4行，新增一个结点70，找到70的父结点为50，新增之后如下图所示
依然符合红黑树的5条规则，因此无须调整，
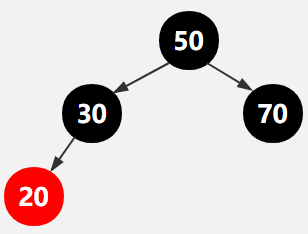
第5行，新增一个结点20，找到20的父结点为30，新增之后如下图所示，
违反了红黑树的规则，红色结点的两个子节点都是黑色。因此我们需要fixAfterInsertion(20)，此处我把元素20标记为x
由于x不为空，且不是根结点，同时满足x的父结点30位红色，我们进入调整的动作，
由于20的父结点30是20父结点的父结点 的左结点，所以我们取到20的父结点的父结点的右结点70，标记为y，
因为y是红色，所以我们把x的父结点变为黑色，y变为黑色，同时把根节点变为红色，同时把x的引用指向x的父结点的父结点，也就是50，
由于50是根，结束调整，最后将50变为黑色，如下图所示
第7行，新增元素40，找到40的父结点30，新增之后如下图所示，
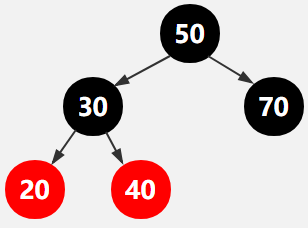
符合红黑树的5条规则，因此不需要调整。
第8-9行新增元素60,80，皆没有破坏红黑树，都不需要调整，如下图所示，
第10行，新增元素85，找到85的父结点为80，新增之后如下图所示，
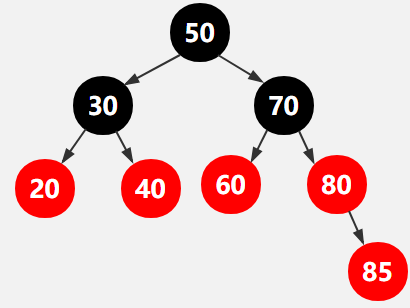
违反了红黑树的规则，红色结点的两个子节点必须为黑色，因此我们需要fixAfterInsertion(85)，此处我把元素85标记为x
由于x满足1.不为空 2.不是根 3.x的父结点为红色，我们进入调整的动作，
由于85的父结点是85父结点的父结点的右结点，所以我们取到85的父结点的父结点的左结点60，记作y，
由于y的颜色为红色，因此，我们把85的父结点80置为黑色，同时把y，即60置为黑色，把85的父结点的父结点，即70变成红色 ，此时x的引用指向x的父结点的父结点，即70，
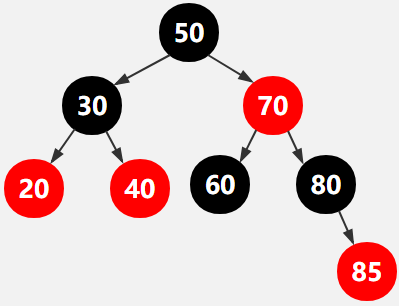
此时，x指向70, 70不满足 父结点是红色，因此不需要调整。
左旋和右旋
我在前面一直提到了左旋转和右旋转，忘记贴上代码，因此，下面我们来逐行阅读左旋和右旋的过程。
1 private void rotateLeft(Entry<K,V> p) { 2 if (p != null) { 3 Entry<K,V> r = p.right; 4 p.right = r.left; 5 if (r.left != null) 6 r.left.parent = p; 7 r.parent = p.parent; 8 if (p.parent == null) 9 root = r; 10 else if (p.parent.left == p) 11 p.parent.left = r; 12 else 13 p.parent.right = r; 14 r.left = p; 15 p.parent = r; 16 } 17 }
预设把待左旋的结点记为p，
第2行，判断该节点是否为空，
第3行，把p的右结点记为r，
第4行，把r的左结点变成p的右结点，
第5-6行，r的左结点不为空时，把r的左结点的父节点变为p,
第7行，把p的父结点变为r的父结点，
第8-13行，如果p本身就是根结点，则把r变为根节点，如果p是父结点的左结点，则把r作为p父结点的左结点，如果p是父结点的右结点，则把r作为p父结点的右结点，
第14行，r的左结点引用指向p，
第15行，p的父结点引用指向r
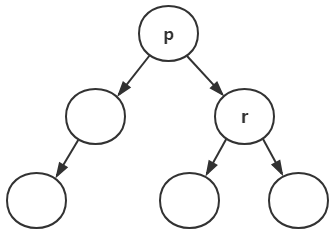
比较简单，我之前用了大量的篇幅讲述了左旋和右旋的的变化，并且画了大量的示意图，
右旋的和左旋刚好相反，源代码如下，我就不再逐行介绍了，
1 private void rotateRight(Entry<K,V> p) { 2 if (p != null) { 3 Entry<K,V> l = p.left; 4 p.left = l.right; 5 if (l.right != null) l.right.parent = p; 6 l.parent = p.parent; 7 if (p.parent == null) 8 root = l; 9 else if (p.parent.right == p) 10 p.parent.right = l; 11 else p.parent.left = l; 12 l.right = p; 13 p.parent = l; 14 } 15 }
TreeMap的remove方法解读
我们在上面建立好的红黑树上，我们跟一下源代码，再来做一下解析和总结，
今天早上醒来翻看微信无意发现一位Java技术界的神跳槽去了阿里，老夫闻之实在是不胜欢喜，这位神一样的人物，对于技术是非常精深与热爱，
老夫我也深受他的启蒙，老夫我的博客也有几天由于工作或者其他各种事情导致断更，今天本来都已就寝，突然脑海里有一种声音在呼唤着，于
是不得不爬起来继续学习，努力在路上....
我们来跟一下remove方法的源码，
1 public V remove(Object key) { 2 Entry<K,V> p = getEntry(key); 3 if (p == null) 4 return null; 5 6 V oldValue = p.value; 7 deleteEntry(p); 8 return oldValue; 9 }
第2行，根据key值得到key对应的结点， getEntry方法根据默认的比较器或者是自定义的比较器，从root根结点开始比较，设当前结点p和key比较，
cmp为比较结果，当cmp>0时，把比较的目标p引用执行p的右结点，cmp<0把比较的目标p引用指向p的左结点，cmp等于0时，该结点就时要查找
的结点
第7行，deleteEntry方法是删除结点的核心方法，如下，
1 private void deleteEntry(Entry<K,V> p) { 2 modCount++; 3 size--; 4 5 // If strictly internal, copy successor's element to p and then make p 6 // point to successor. 7 if (p.left != null && p.right != null) { 8 Entry<K,V> s = successor(p); 9 p.key = s.key; 10 p.value = s.value; 11 p = s; 12 } // p has 2 children 13 14 // Start fixup at replacement node, if it exists. 15 Entry<K,V> replacement = (p.left != null ? p.left : p.right); 16 17 if (replacement != null) { 18 // Link replacement to parent 19 replacement.parent = p.parent; 20 if (p.parent == null) 21 root = replacement; 22 else if (p == p.parent.left) 23 p.parent.left = replacement; 24 else 25 p.parent.right = replacement; 26 27 // Null out links so they are OK to use by fixAfterDeletion. 28 p.left = p.right = p.parent = null; 29 30 // Fix replacement 31 if (p.color == BLACK) 32 fixAfterDeletion(replacement); 33 } else if (p.parent == null) { // return if we are the only node. 34 root = null; 35 } else { // No children. Use self as phantom replacement and unlink. 36 if (p.color == BLACK) 37 fixAfterDeletion(p); 38 39 if (p.parent != null) { 40 if (p == p.parent.left) 41 p.parent.left = null; 42 else if (p == p.parent.right) 43 p.parent.right = null; 44 p.parent = null; 45 } 46 } 47 }
把待删除的结点设为p，
第2-3行，modCount自增，size自减，
第5-6行，注释，If strictly internal, copy successor's element to p and then make p， point to successor.，直译过来就是：如果严格的内部，赋值p的继承者，同时把p的引用指向p的继承者，
第7-12行，如果p的左结点和右结点都不为空，则寻找p的继承者，
第8行，successor()方法，右结点不为空，往右子树查找最小的结点，右结点为空时，作别的查找，此处，p的右结点必定不为空的情况，为空情况稍微有点复杂，下面会有个专门的版块讲解，
第9-11行，把p指向继承者。
未完待续.....
