从树型结构谈到红黑树的概念以及在源码中的应用
原文地址http://www.cnblogs.com/sunshine798798/p/9075848.html,转载请注明出处,谢谢!
树型结构
什么是树型结构呢?
树型结构指的是数据元素之间存在一对多的树型关系的数据结构,是一类非线性的数据结构,
下面先来看一个简单的树型结构图,
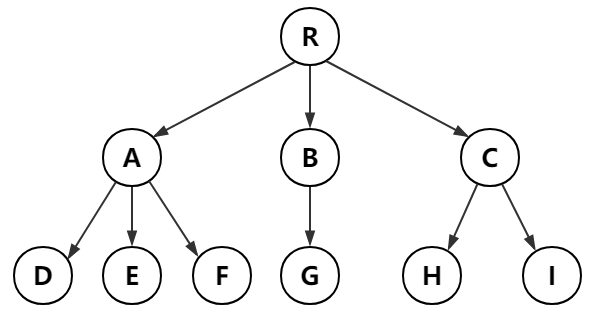
从上图,我们可以清楚的知道,树型结构指的就是数据元素的集合,那么这些数据元素我们称之为“结点”,
1.结点:树型结构中的任何一个数据元素都称之为结点,如图中R、A、B、C、D、E、F、G、H、I
2.根:最上面的结点是树的根,也叫根结点,一个树型结构有且仅有一个根结点,如图示中R,其他结点都是根据根结点发展而来,
3.父结点:当前结点的上一个结点称为该结点的父结点。如图中D结点的父结点是A结点,H结点的父结点是C结点,
4.子结点:和父结点相反,如图中的D结点是A结点的子结点,
5.兄弟结点:具有相同父结点的所有结点是兄弟结点,如图中DEF的父结点都是结点A,因此DEF是兄弟结点,
6.结点的度:当前结点拥有子结点的个数称为该结点的度,如图中A的度为3,
7.树叶:没有子结点的结点叫树叶,如图中 DEFGHI
8.分支结点:除了树叶之外,其他的所有结点,包括根结点都是分支结点,
9.结点的层次:规定根结点的层次为1,它的子结点层次为2,以此类推
10.树的深度:最大层次树,如图中最大层次树为3
二叉树
二叉树是一类特殊的树结构,在基本树形态的基础上,只要满足树中任何一个结点的子结点不超过2个,
那该树称之为二叉树,如下图
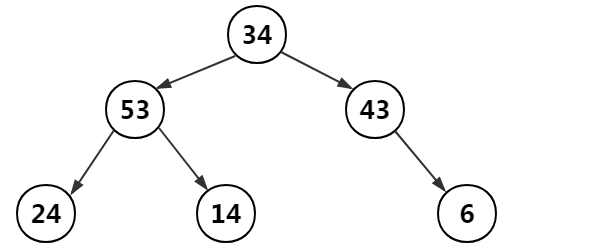
二叉查找树
二叉查找树是在二叉树的基础上,我们增加约束条件,在树型结构中的任何一个结点a,他的左子树b,他的右子树c,满足 b<a 且 c>a的树,
称为二叉查找树。如下示意图,
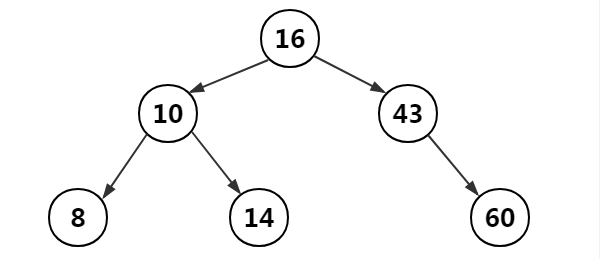
例如我需要查找14
第一步:由于14 <16,所以查找左子树
第二步:由于14 >10,所以查找右子树
第三步:发现10的右子树就是14
这种方式也正是二分查找的思想。
在二叉树查找树的极端情况下,举个例子,在树结构中依次存储数据元素 43 32 31 28 12,树形态如下图
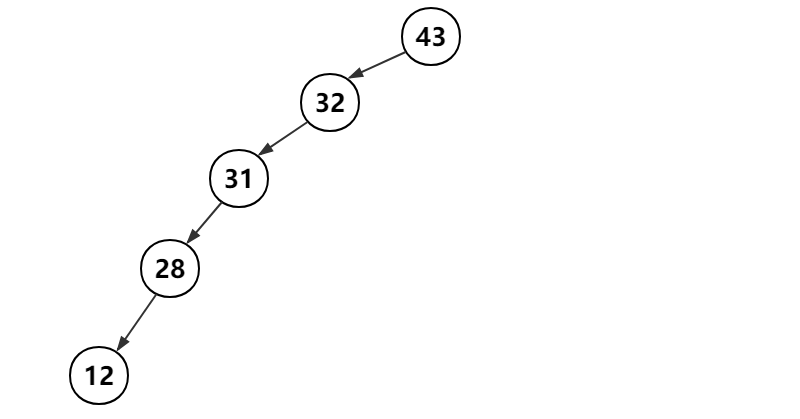
我们称为这种形态的树为只有左子树的不平衡树,反之称为只有右子树的不平衡树。
红黑树的概念
以上从普通树结构谈到二叉树,以及二叉查找树。在极端情况下,还是难以避免树结构失去平衡,红黑树的出现就是为了保证树结构的平衡,
那什么是红黑树呢?
红黑树(Red Black Tree)是一种自平衡的二叉树,
除了二叉树所有拥有的性质之外,还具有以下独有的性质
1.结点是红色或者黑色,
2.根结点为黑色,
3.每个叶子结点都是黑色的空结点,
4.每个红色结点的两个子结点都是黑色,
5.从任何一个结点到叶子结点的所有路径的黑色结点的个数相同。
如下图中的树结构,就是一颗典型的红黑树。
也是因为上面5条规则才保证了红黑树的自平衡,红黑树从根结点到叶子结点的最长路径不会超过最短路径的2倍。
下面我们来简单的举两个例子说明红黑树是如何保持自平衡。
第一个例子:向原红黑树插入数据为45的结点,
由于45结点的插入,并没有破坏红黑树的5条规则,因此并不会红黑树的平衡。
第二个例子:向原红黑树插入数据为72的结点
由于72的父结点为红色结点,这破坏了红黑树规则4.每个红色结点的两个子结点都是黑色,因此红黑树需要通过一定的调整保持树结构的平衡,
调整的方式有两种,一种是旋转,另外一种是变色,而自旋转有分为左旋转和右旋转,
红黑树变色
为了使红黑树重新符合规则,我们尝试将黑色结点变为红色,将红色结点变为黑色。
因为72与75同为红色,不符合规则4.每个红色结点的两个子节点都是黑色,因此我们将结点75变为黑色,如下图,
但是还没有结束,结点75和父结点80同为黑色,破坏了规则5.从任何一个结点到叶子结点的所有路径的黑色结点的个数相同。
我们尝试把结点80变为红色,此时结点80和结点85同为红色,不满足规则4.每个红色结点的两个子结点都是黑色, 于是把85变为黑色,如下图,
此时结点80和父结点70同为红色,如果将结点70变为黑色,那根结点只能变成红色,这和规则根结点必须为黑色不符合,变色似乎很难解决红黑树的平衡问题,
我们想到了旋转。那么什么是旋转呢?
红黑树旋转
红黑树的旋转分为1.左旋转 2.右旋转
左旋转是将两个红黑树的结点逆时针旋转。使得右结点旋转成为父结点,而原来的父结点称为左结点,如下图所示,
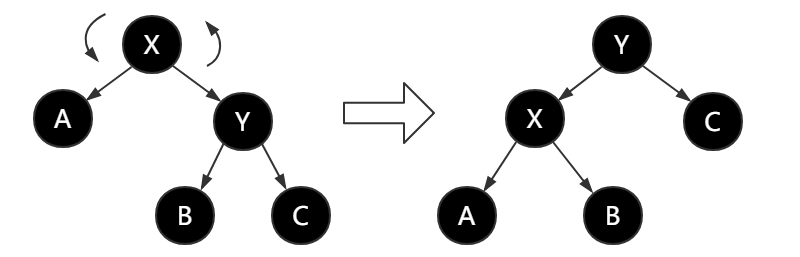
由上图,我们可以得出,将结点X左旋,使得结点Y成为X的父结点,而X成为Y的左结点,Y的左结点B称为X结点的右结点,这就是左旋转
右旋转是将两个红黑树的结点顺时针旋转,使得左结点旋转成为父结点。而原来的父结点成为右结点,如下图所示,
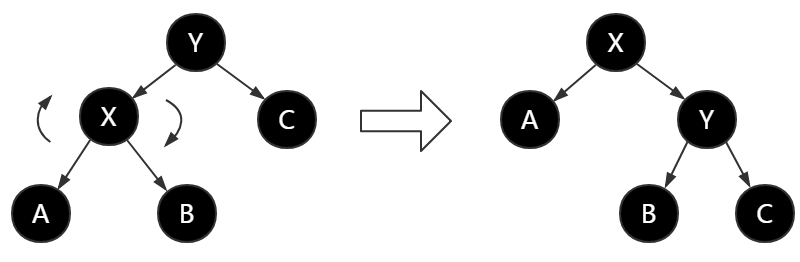
我们尝试着将刚才的树结构左旋转,如下图所示,
此时根据规则我们把根节点70变为黑色,50变为红色,30变为黑色,20,40变为红色,28变为黑色
这样就结束了吗?并没有,其中有两条路径的黑色结点个数为4个,而其他路径的黑色结点为3个,违反了红黑树规则5.从任何一个结点到叶子结点的所有路径的黑色结点的个数相同。
于是我们继续对结点50右旋转,用来降低结点28的层次,如下图所示,
下面对树结构进行变色30变成红色,20,50变成黑色,28,60变成红色,
这就是第一颗自平衡以后的标准红黑树,理论知识暂时先介绍到这里。
红黑树在JDK源代码中的应用
红黑树在JDK源代码中的应用最典型的就是TreeMap,以及Java 8中的Hashmap,
由于篇幅的原因,源代码我会在下一篇讲解。


