XX Open Cup, Grand Prix of Korea【杂题】
很喜欢 Alpha1022 的一句话:Open Cup 还是一场场做比较有感觉 。
。
A. 6789
给定一个 \(n \times m\) 的矩阵,每个位置上有一张写着 \(6,7,8\) 或 \(9\) 的卡牌。求最少反转多少张卡牌使得将矩阵反转 \(180^{\circ}\) 后和原来相同,或判断无解。
\(n,m \leq 500\)。
模拟。
code
#include <bits/stdc++.h>
using namespace std;
const int N = 5e2 + 5;
int n, m, ans; char s[N][N];
void chk(char c1, char c2) {
if (c1 == '6' && c2 == '9' || c1 == '9' && c2 == '6' || c1 == '8' && c2 == '8') return;
if (c1 == c2) return ans++, void();
puts("-1"), exit(0);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) scanf("%s", s[i] + 1);
for (int i = 1; i <= n / 2; i++) {
for (int j = 1; j <= m / 2; j++) chk(s[i][j], s[n - i + 1][m - j + 1]);
for (int j = (m + 1) / 2 + 1; j <= m; j++) chk(s[i][j], s[n - i + 1][m - j + 1]);
}
if (n & 1) for (int j = 1; j <= m / 2; j++) chk(s[n / 2 + 1][j], s[n / 2 + 1][m - j + 1]);
if (m & 1) for (int i = 1; i <= n / 2; i++) chk(s[i][m / 2 + 1], s[n - i + 1][m / 2 + 1]);
if ((n & 1) && (m & 1))
if (s[n / 2 + 1][m / 2 + 1] != '8') return puts("-1"), 0;
cout << ans << endl;
return 0;
}
B. Bigger Sokoban 40k
推 \(2 \times 2\) 箱子游戏,构造一个 \(n \times m\) 的地图使得移动步数不小于 \(4 \times 10^4\)。你需要保证 \(n + m \leq 100\)。
观察下面这个从官方题解贺来的图:

玩家想要改变推箱子的方向,就不得不绕过整个地图。把尽量多的这种拐弯拼起来就行了。
由于俺不会写代码,于是就手造了一个,感觉很趣味(
code
51 47
.....##########################################
.##P.##...#.............#...#.............#...#
.#.BB.....#.................#.................#
.#.BB.....#.................#.................#
.#....#...##..#.........#...##..#.........#...#
.######..###..###########..###..###########..##
.#...##..##...#....#...##..##...#....#...##..##
.#........#........#........#........#........#
.#........#........#........#........#........#
.#...#....#...##..##...#....#...##..##...#....#
.##..###########..###..###########..###..######
.##..##...#....#...##..##...#....#...##..##...#
.#........#........#........#........#........#
.#........#........#........#........#........#
.#....#...##..##...#....#...##..##...#....#...#
.######..###..###########..###..###########..##
.#...##..##...#....#...##..##...#....#...##..##
.#........#........#........#........#........#
.#........#........#........#........#........#
.#...#....#...##..##...#....#...##..##...#....#
.##..###########..###..###########..###..######
.##..##...#....#...##..##...#....#...##..##...#
.#........#........#........#........#........#
.#........#........#........#........#........#
.#....#...##..##...#....#...##..##...#....#...#
.######..###..###########..###..###########..##
.#...##..##...#....#...##..##...#....#...##..##
.#........#........#........#........#........#
.#........#........#........#........#........#
.#...#....#...##..##...#....#...##..##...#....#
.##..###########..###..###########..###..######
.##..##...#....#...##..##...#....#...##..##...#
.#........#........#........#........#........#
.#........#........#........#........#........#
.#....#...##..##...#....#...##..##...#....#...#
.######..###..###########..###..###########..##
.#...##..##...#....#...##..##...#....#...##..##
.#........#........#........#........#........#
.#........#........#........#........#........#
.#...#....#...##..##...#....#...##..##...#....#
.##..###########..###..###########..###..######
.##..##...#....#...##..##...#....#...##..##...#
.#........#........#........#........#........#
.#........#........#........#........#........#
.#....#...##..##...#....#...##..##...#....#...#
.######..###...##########..###...##########..##
.#...#.........#...#...#.........#...#...#....#
.#...#.........#...#...#.........#...#...#SS..#
.#...#....##...#...#...#....##...#...#...#SS..#
.############################################.#
...............................................
C. Cleaning
给定一个 \(n \times m\) 的网格图,每个位置上有一个方向,表示在该位置时不能朝该方向走。
\(q\) 次询问,每次给定 \(a,b,c,d\),求有多少格子在至少一条 \((a,b)\) 到 \((c,d)\) 的路径上。
\(n,m \leq 10^3\),\(q \leq 3 \times 10^5\)。
这是一个可达性相关问题,考虑先求出所有的强连通分量并按拓扑序排序。
性质 \(1\):按拓扑序依次加入所有强连通分量,在任意时刻所形成的图形都是若干个不相邻的矩形。
证明:若某个图形 \(G\) 不是矩形,则 \(G\) 外一定存在一个位置与 \(G\) 的至少两条边相邻,因此这个位置向 \(G\) 有至少一条边,与拓扑序矛盾。
考虑在按拓扑序加入的过程中维护图的变化。在维护的过程中我们不保证图形是若干个不相邻的矩形,而可以是若干个矩形并排。加入一个强连通分量 \(G\) 后,我们进行如下操作:
-
从包含 \(G\) 的最小矩形内部的所有矩形向 \(G\) 连 树边。
-
处理上下左右四个方向的矩形。以右方为例,我们建一个虚点,对所有右方紧贴着的矩形向虚点连 树边,并从虚点向 \(G\) 连 非树边。特别地,如果所有矩形的左边界都是
L则不连边。
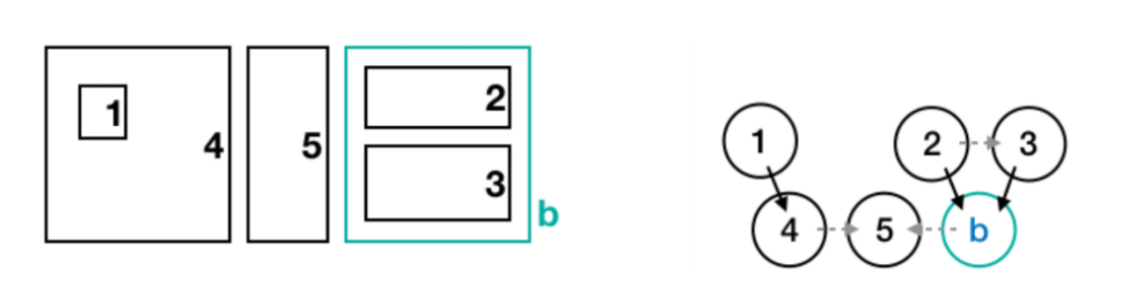
为了说明这张图和原来的图等价,需要证明如下性质:
性质 \(2\):在任意时刻,对于并排的若干个矩形和任意垂直于并排方向的方向,要么矩形内的所有小格都能从该方向离开矩形,要么都不能。
证明:考虑归纳:
-
对于强连通分量 \(G\) 和其内部的矩形合并成的矩形,以上方为例,有两种情况:
- 若上边界所有位置都在 \(G\) 内,则由连通性结论显然。
- 若上边界存在某些位置在 \(G\) 外,设为矩形 \(Q\),若 \(Q\) 能从上方离开而 \(G\) 不能,则 \(G\) 上边界的所有位置都是
U。因此一定存在上边界的某个位置可以通过左右移动进入 \(Q\),这与拓扑序矛盾。
-
对于 \(G\) 和某个边界紧贴的矩形并排的情况,以左右并排,从下方离开为例:若存在一个矩形无法从下方离开,那么其下边界所有位置都是
D。因此其一定能够通过左右移动进入紧贴着的其他矩形,于是结论显然成立。
于是我们成功得到了一颗树的结构,且每个点的儿子被连成了若干条有向链。此时可达点计数是简单的:只需要从起点往上跳到深度等于终点的祖先,它们一定有同一个父亲。检查这两个点是否被同一条链相连即可。
使用并查集维护建树过程,倍增回答询问,记 \(r = n \times m\),则时间复杂度为 \(O(r \alpha(r) + q \log r)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef vector <int> vi;
typedef pair <int, int> pi;
#define pb emplace_back
const int N = 1e6 + 5;
const int dx[] = {0, 0, -1, 1}, dy[] = {-1, 1, 0, 0};
int n, m, q, d[N];
int tim, cnt, bel[N], dfn[N], low[N]; vi stk;
int xMi[N], xMx[N], yMi[N], yMx[N], sz[2 * N]; vi vr[N];
void tarjan(int u) {
dfn[u] = low[u] = tim++;
stk.pb(u);
int ux = u / m, uy = u % m;
for (int k = 0; k < 4; k++) {
if (k == d[u])
continue;
int vx = ux + dx[k], vy = uy + dy[k];
if (vx < 0 || vx >= n || vy < 0 || vy >= m)
continue;
int v = vx * m + vy;
if (dfn[v] == -1) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (bel[v] == -1) {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
int v;
do {
v = stk.back();
stk.pop_back();
bel[v] = cnt;
} while (v != u);
cnt++;
}
}
int f[2 * N], par[2 * N];
int gf(int x) {
while (x != f[x]) x = f[x] = f[f[x]];
return x;
}
int root;
vi e[2 * N];
int dep[2 * N], dir[2 * N], sum[2 * N], le[2 * N], ri[2 * N], val[2 * N], ch[2 * N], cp[2 * N];
vector <pi> E;
int p[2 * N][21], pos[2 * N], deg[2 * N];
void dfs(int u) {
p[u][0] = par[u];
for (int i = 1; (1 << i) <= dep[u]; i++)
p[u][i] = p[p[u][i - 1]][i - 1];
for (auto v : e[u]) {
dep[v] = dep[u] + 1;
dfs(v);
}
}
void dfs2(int u) {
if (e[u].empty())
return;
int d = e[u].size();
for (int i = 0, x = 0; i < d; i++) {
int v = e[u][i];
x += sz[v];
sum[v] = x;
}
for (int i = 0; i < d; i++) {
int v = e[u][i];
if (i == 0 || dir[e[u][i - 1]] != -1) {
le[v] = v;
} else {
le[v] = le[e[u][i - 1]];
}
}
for (int i = d - 1; i >= 0; i--) {
int v = e[u][i];
if (dir[v] != 1) {
ri[v] = v;
} else {
ri[v] = ri[e[u][i + 1]];
}
}
for (auto v : e[u])
val[v] = sum[ri[v]] - sum[le[v]] + sz[le[v]];
for (auto v : e[u]) {
val[v] += val[u];
dfs2(v);
}
}
int qry(int a, int b) {
if (dep[a] < dep[b])
return 0;
int ret = val[a];
for (int i = 20; i >= 0; i--)
if (dep[a] - (1 << i) >= dep[b])
a = p[a][i];
ret -= val[a];
if (par[a] != par[b])
return 0;
if (pos[a] < pos[b]) {
if (pos[ri[a]] >= pos[b]) {
return sum[b] - sum[a] + ret + sz[a];
} else {
return 0;
}
} else {
if (pos[le[a]] <= pos[b]) {
return sum[a] - sum[b] + ret + sz[b];
} else {
return 0;
}
}
}
int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> q;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < m; j++) {
int u = i * m + j;
if (s[j] == 'L') {
d[u] = 0;
} else if (s[j] == 'R') {
d[u] = 1;
} else if (s[j] == 'U') {
d[u] = 2;
} else {
d[u] = 3;
}
}
}
fill(dfn, dfn + n * m, -1);
fill(bel, bel + n * m, -1);
for (int i = 0; i < n * m; i++)
if (dfn[i] == -1)
tarjan(i);
for (int i = 0; i < n * m; i++)
vr[bel[i]].pb(i);
for (int i = 0; i < cnt; i++) {
xMi[i] = yMi[i] = N;
xMx[i] = yMx[i] = -1;
for (auto u : vr[i]) {
int x = u / m, y = u % m;
xMi[i] = min(xMi[i], x);
xMx[i] = max(xMx[i], x);
yMi[i] = min(yMi[i], y);
yMx[i] = max(yMx[i], y);
}
sz[i] = vr[i].size();
}
for (int i = 0; i < 2 * N; i++)
f[i] = i;
for (int c = cnt - 1; c >= 0; c--) {
for (auto u : vr[c]) {
int ux = u / m, uy = u % m;
for (int k = 0; k < 4; k++) {
int vx = ux + dx[k], vy = uy + dy[k];
if (vx < xMi[c] || vx > xMx[c] || vy < yMi[c] || vy > yMx[c])
continue;
int v = vx * m + vy;
v = gf(bel[v]);
if (v != c)
par[v] = f[v] = c;
}
}
for (auto x : {xMi[c] - 1, xMx[c] + 1}) {
if (x < 0 || x >= n || bel[x * m + yMi[c]] < c)
continue;
bool all = 1;
int u = gf(bel[x * m + yMi[c]]);
bool fl = 1;
for (int y = yMi[c]; y <= yMx[c]; y++) {
int v = x * m + y;
if (d[v] != (x < xMi[c] ? 3 : 2))
all = 0;
v = gf(bel[v]);
if (gf(v) != u) {
if (fl) {
par[u] = f[u] = cnt;
u = cnt++;
fl = 0;
}
par[v] = f[v] = u;
}
}
if (!all) {
E.pb(u, c);
deg[u]++, ch[u] ^= c;
deg[c]++, ch[c] ^= u;
}
}
for (auto y : {yMi[c] - 1, yMx[c] + 1}) {
if (y < 0 || y >= m || bel[xMi[c] * m + y] < c)
continue;
bool all = 1;
int u = gf(bel[xMi[c] * m + y]);
bool fl = 1;
for (int x = xMi[c]; x <= xMx[c]; x++) {
int v = x * m + y;
if (d[v] != (y < yMi[c] ? 1 : 0))
all = 0;
v = gf(bel[v]);
if (gf(v) != u) {
if (fl) {
par[u] = f[u] = cnt;
u = cnt++;
fl = 0;
}
par[v] = f[v] = u;
}
}
if (!all) {
E.pb(u, c);
deg[u]++, ch[u] ^= c;
deg[c]++, ch[c] ^= u;
}
}
}
root = cnt;
for (int i = 0; i < cnt; i++)
if (f[i] == i)
par[i] = f[i] = root;
for (int i = 0; i < cnt; i++)
e[par[i]].pb(i);
cnt++;
par[root] = -1;
dfs(root);
fill(pos, pos + cnt, -1);
for (int i = 0; i < cnt - 1; i++) {
if (pos[i] != -1)
continue;
if (deg[i] == 0) {
pos[i] = cp[par[i]]++;
} else if (deg[i] == 1) {
int u = i, v = 0, p = par[u];
do {
pos[u] = cp[p]++;
v ^= ch[u];
swap(u, v);
} while (deg[u] == 2);
pos[u] = cp[p]++;
}
}
for (int i = 0; i < cnt - 1; i++)
e[par[i]][pos[i]] = i;
for (auto [a, b] : E) {
if (pos[a] < pos[b]) {
dir[a] = 1;
} else {
dir[b] = -1;
}
}
dfs2(root);
while (q--) {
int a, b, c, d;
cin >> a >> b >> c >> d;
a--;
b--;
c--;
d--;
int u = bel[a * m + b];
int v = bel[c * m + d];
cout << qry(u, v) << "\n";
}
return 0;
}
D. Container
给定两个长为 \(n\) 的序列 \(a,b\),序列中只包含 \(1\) 和 \(2\)。
每次操作可以选择 \(a\) 的一个长度为 \(2\) 或 \(3\) 的区间 \([l,r]\),然后将它翻转。一次操作的代价为 \(c + \sum \limits_{i=l}^r a_i\)。
求使得 \(a\) 和 \(b\) 相同的最小代价,并构造方案。
\(n \leq 100\),\(c \leq 10^3\)。
显然可以只考虑 \([2,1,1] \stackrel{c+4}{\longleftrightarrow} [1,1,2]\),\([1,2] \stackrel{c+3}{\longleftrightarrow} [2,1]\),\([2,2,1] \stackrel{c+5}{\longleftrightarrow} [1,2,2]\) 这三种操作。
不妨分别称这三种操作为操作 \(1\),操作 \(2\),和操作 \(3\)。
我们可以只考虑 \(2\) 的移动,这是因为当所有的 \(2\) 都复原之后 \(1\) 显然也都复原了。把 \(a\) 和 \(b\) 中的 \(2\) 一一匹配后,设它们之间的距离为 \(d_1,d_2,\cdots,d_k\)(其中 \(k\) 为 \(2\) 的个数),设逆序对数为 \(z\),则我们可以得到答案的一个下界: \(z + \sum \limits_{i=1}^k \left( \lfloor \frac{d_i}{2} \rfloor \cdot (c+4) + (d_i \ \text{mod} \ 2) \cdot (c+3) \right)\)。
这是因为,我们可以通过操作 \(1\) 使一个 \(2\) 移动两步,通过操作 \(2\) 使一个 \(2\) 移动一步。而每有一个逆序对,就需要将一个操作 \(2\) 改成操作 \(3\),从而额外产生 \(1\) 的代价。可以证明这个下界是能够取到的。
但这个式子的最小值仍然不好直接计算,我们需要进一步观察匹配的性质。
考虑一个特殊的情况:若 \(b\) 中所有 \(2\) 的位置奇偶性相同,那么此时无论 \(a\) 如何匹配,操作 \(2\) 的贡献都是确定的。于是此时只需要最小化 \(z + \sum \limits_{i=1}^k \lfloor \frac{d_i}{2} \rfloor\) 的值即可。通过调整法容易说明,将 \(a\) 和 \(b\) 从小到大依次匹配是最优的,此时 \(z\) 和 \(\sum \limits_{i=1}^k \lfloor \frac{d_i}{2} \rfloor\) 都取到了最小值。
类似地,对于一般情况,我们将 \(b\) 中所有 \(2\) 的位置分成两个集合 \(B_0\) 和 \(B_1\),其中 \(B_0\) 中的位置都是偶数,\(B_1\) 中的位置都是奇数。假设我们已经确定了 \(a\) 中所有 \(2\) 的位置的一个划分 \(A_0\) 和 \(A_1\),使得 \(A_0\) 和 \(B_0\),\(A_1\) 和 \(B_1\) 内部匹配,那么最优的匹配方式是让两个部分分别从小到大依次匹配。
简单证明一下:由上面的讨论我们知道此时 \(A_0\) 和 \(B_0\),\(A_1\) 和 \(B_1\) 内部代价都是最小的,只需要考虑两个部分之间产生的逆序对数。通过调整容易说明这样匹配后两个部分之间的逆序对数也是最小的,因此结论成立。
于是可以考虑 DP,设 \(f_{i,j}\) 为考虑了 \(a\) 中前 \(i\) 个 \(2\) 的位置,其中有 \(j\) 个划分到 \(A_0\),\(i-j\) 个划分到 \(A_1\),转移是简单的。通过记录最优决策点及拓扑排序容易构造方案,总时间复杂度 \(O(n^2)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef pair <int, int> pi;
#define pb emplace_back
const int N = 505, inf = 1e9;
int n, c;
string s, t;
vector <int> a, b[2];
int sum[N][N], f[N][N], g[N][N], e[N][N];
int v[N], deg[N];
queue <int> q;
vector <pi> ans;
void dfs(int x, int y) {
if (x == 0)
return;
if (g[x][y] == 0) v[x - 1] = b[0][y - 1], x--, y--;
else v[x - 1] = b[1][x - y - 1], x--;
dfs(x, y);
}
int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> c >> s >> t;
for (int i = 0; i < n; i++) {
if (s[i] == '2') a.pb(i);
if (t[i] == '2')
b[i % 2].pb(i), sum[i % 2][i]++;
}
for (int i = 0; i < n; i++) {
sum[0][i] += sum[0][i - 1];
sum[1][i] += sum[1][i - 1];
}
int m = a.size();
for (int i = 0; i <= m; i++)
for (int j = 0; j <= m; j++)
f[i][j] = inf;
f[0][0] = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j <= i; j++) {
if (f[i][j] == inf)
continue;
if (j < b[0].size()) {
int x = b[0][j];
int d = abs(a[i] - x);
int val = f[i][j] + (d / 2) * (c + 4) + (d % 2) * (c + 3);
int w = max(0, sum[1][x] - (i - j));
val += w;
if (val < f[i + 1][j + 1]) {
f[i + 1][j + 1] = val;
g[i + 1][j + 1] = 0;
}
}
if (i - j < b[1].size()) {
int x = b[1][i - j];
int d = abs(a[i] - x);
int val = f[i][j] + (d / 2) * (c + 4) + (d % 2) * (c + 3);
int w = max(0, sum[0][x] - j);
val += w;
if (val < f[i + 1][j]) {
f[i + 1][j] = val;
g[i + 1][j] = 1;
}
}
}
}
dfs(m, b[0].size());
for (int i = 0; i < m; i++)
for (int j = 0; j < i; j++) if (v[i] > v[j]) {
if (a[i] <= v[j]) {
e[i][j] = 1, deg[j]++;
}
if (a[j] >= v[i]) {
e[j][i] = 1, deg[i]++;
}
}
for (int i = 0; i < m; i++)
if (deg[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front();
q.pop();
if (a[u] < v[u]) {
while (a[u] + 2 <= v[u]) {
ans.pb(a[u] + 1, a[u] + 3), a[u] += 2;
}
if (a[u] < v[u])
ans.pb(a[u] + 1, a[u] + 2);
} else {
while (a[u] - 2 >= v[u]) {
ans.pb(a[u] - 1, a[u] + 1), a[u] -= 2;
}
if (a[u] > v[u])
ans.pb(a[u], a[u] + 1);
}
for (int v = 0; v < m; v++)
if (e[u][v] && --deg[v] == 0) q.push(v);
}
cout << ans.size() << "\n";
for (auto [x, y] : ans)
cout << x << " " << y << "\n";
return 0;
}
E. Dead Cacti Society
给定一棵 \(n\) 个点 \(m\) 条边的仙人掌,你需要割掉其中的一些边使其变成一棵树。
其中 \(i\) 号点有治愈系数 \(p_i\),第 \(i\) 条边有长度 \(c_i\),治愈系数 \(q_i\)。若割掉了边 \(e_i = \{u,v\}\),那么会新生成一个点 \(u'\) 和 \(u\) 连接,边权为 \(p_u + q_i\)。点 \(v\) 同理。
求最后生成的树的直径的最小值。
\(n \leq 10^5\),\(n \leq m \leq 1.5 \times 10^5\),\(c_i,p_i,q_i \leq 10^9\),时限 \(\text{10.0s}\)。
直径就是树上所有点对距离的最大值,所以我们其实是要求一个最大值的最小值,考虑二分。
我们先对仙人掌分解成环和单点,它们形成一颗树的结构。然后对于当前二分的 \(\text{mid}\),我们按照如下方式判断:我们对所有点求出 \(d_u\) 表示考虑完了 \(u\) 子树内的所有环,此时 \(u\) 子树内直径 \(\leq \text{mid}\),在这种情况下 \(u\) 子树深度的最小值。
-
对于单点,我们将其儿子的 \(d\) 合并,如果最长距离 \(\leq \text{mid}\) 就更新 \(d_u\),否则不合法。
-
对于环,我们枚举断开哪条边,然后分类讨论 DP 合并出经过环的最长距离,如果它 \(\leq \text{mid}\) 就更新 \(d_u\)。
最后检查所有 \(d_i\) 是否都 \(\leq \text{mid}\) 即可。环上需要分类讨论的情况有点多,因为我是懒狗所以这里就不赘述了,具体还是看代码吧(
总时间复杂度 \(O((n+m) \log V)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair <int, LL> pi;
#define mp make_pair
#define fi first
#define se second
#define pb push_back
const int N = 2e5 + 5;
const LL inf = 1e18;
int n, m, rv[N], re[N], w[N]; vector <pi> g[N], t[N];
int tim, dfn[N], low[N], stk[N], tp, cnt;
int id[N]; LL lim, l[N], r[N], d[N], ld[N], rd[N], lf[N], rf[N], lg[N], rg[N], lh[N], rh[N], ans; bool ok;
vector <int> bl, e;
map <pi, int> f;
LL min(LL x, LL y) { return x < y ? x : y; }
LL max(LL x, LL y) { return x > y ? x : y; }
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
stk[++tp] = u;
for (auto [v, w] : g[u]) if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] == dfn[u]) {
if (stk[tp] == v) { t[u].pb(mp(v, w)), t[v].pb(mp(u, w)); tp--; continue; }
++cnt; int lst = u;
for (int x = 0, _w; x != v; tp--) {
x = stk[tp], _w = f[mp(lst, x)];
t[cnt].pb(mp(x, _w)), t[x].pb(mp(cnt, _w));
lst = x;
}
int _w = f[mp(u, lst)];
t[cnt].pb(mp(u, _w));
t[u].pb(mp(cnt, _w));
}
} else low[u] = min(low[u], dfn[v]);
}
void dfs(int u, int ff) {
d[u] = inf;
for (auto [v, w] : t[u]) if (v != ff) dfs(v, u);
if (u > n) {
bl.clear(), e.clear();
bl.pb(ff);
for (auto [v, w] : t[u]) bl.pb(v), e.pb(w);
int L = e.size();
for (int i = 1; i < L; i++) l[i] = l[i - 1] + w[e[i - 1]];
for (int i = 1; i < L; i++) ld[i] = max(ld[i - 1], d[bl[i]] + l[i]);
for (int i = 1; i < L; i++) lf[i] = max(lf[i - 1], d[bl[i]] - l[i]);
for (int i = 1; i < L; i++) lh[i] = max(lh[i - 1] + w[e[i - 1]], d[bl[i]]);
for (int i = 2; i < L; i++) lg[i] = max(lg[i - 1], lf[i - 1] + (d[bl[i]] + l[i]));
for (int i = L; i > 1; i--) r[i] = r[i + 1] + w[e[i - 1]];
for (int i = L - 1; i; i--) rd[i] = max(rd[i + 1], d[bl[i]] + r[i + 1]);
for (int i = L - 1; i; i--) rf[i] = max(rf[i + 1], d[bl[i]] - r[i + 1]);
for (int i = L - 1; i; i--) rh[i] = max(rh[i + 1] + w[e[i]], d[bl[i]]);
for (int i = L - 2; i; i--) rg[i] = max(rg[i + 1], rf[i + 1] + (d[bl[i]] + r[i + 1]));
for (int i = 1; i <= L; i++) {
LL w1 = rv[bl[i - 1]] + re[e[i - 1]];
LL w2 = rv[bl[i]] + re[e[i - 1]];
LL r1 = lg[i - 1];
LL r2 = rg[i];
LL r3 = ld[i - 1] + rd[i];
LL r4 = w1 + max(lh[i - 1], l[i - 1] + rd[i]);
LL r5 = w2 + max(rh[i], r[i + 1] + ld[i - 1]);
LL r6 = w1 + l[i - 1] + r[i + 1] + w2;
LL R = max({r1, r2, r3, r4, r5, r6});
if (R <= lim) {
LL d1 = ld[i - 1];
LL d2 = rd[i];
LL d3 = w1 + l[i - 1];
LL d4 = w2 + r[i + 1];
LL D = max({d1, d2, d3, d4});
d[u] = min(d[u], D);
}
}
fill(l + 1, l + L + 1, 0);
fill(ld + 1, ld + L + 1, 0);
fill(lf + 1, lf + L + 1, 0);
fill(lg + 1, lg + L + 1, 0);
fill(lh + 1, lh + L + 1, 0);
fill(r + 1, r + L + 1, 0);
fill(rd + 1, rd + L + 1, 0);
fill(rf + 1, rf + L + 1, 0);
fill(rg + 1, rg + L + 1, 0);
fill(rh + 1, rh + L + 1, 0);
} else {
LL d1 = 0, d2 = 0;
for (auto [v, i] : t[u]) if (v != ff) {
LL D = d[v] + (v > n ? 0 : w[i]);
if (D > d1) d2 = d1, d1 = D;
else if (D > d2) d2 = D;
}
LL D = d1 + d2;
if (D > lim) ok = 0;
d[u] = d1;
}
if (d[u] > lim) ok = 0;
}
bool check(LL mid) {
fill(d + 1, d + cnt + 1, 0);
lim = mid, ok = 1, dfs(1, 0);
return ok;
}
int main() {
ios :: sync_with_stdio(0);
cin >> n >> m; cnt = n;
for (int i = 1; i <= n; i++) cin >> rv[i];
LL l = 0, r = 0;
for (int i = 1, u, v; i <= m; i++) {
cin >> u >> v >> w[i] >> re[i];
g[u].pb(mp(v, i)), g[v].pb(mp(u, i));
r = max(r, w[i]);
r = max(r, max(rv[u] + re[i], rv[v] + re[i]));
f[mp(u, v)] = f[mp(v, u)] = i;
}
tarjan(1);
r *= (n - 1 + 2 * (m - n + 1));
while (l <= r) {
LL mid = (l + r) >> 1;
if (check(mid)) r = mid - 1, ans = mid;
else l = mid + 1;
}
cout << ans << "\n";
return 0;
}
F. Hilbert's Hotel
小 A 开了一个酒店,其中有无数个房间,编号分别为 \(0,1,2,\cdots\),每个房间只能住一个人。
酒店只接待团队入住。酒店有一个团队编号 \(G\),所有入住的团队按照顺序从 \(1\) 开始标号。
当有新的团队到达酒店时,小 A 将会按照如下规则安排房间:
- 若有 \(k\) 个人到达酒店,那么对于每个房间 \(x\),其中的客人将移动到房间 \(x+k\)。之后,新客人填满 \(0 \sim k−1\) 的所有房间。
- 若有无数个人到达酒店,那么对于每个房间 \(x\),其中的客人将移动到房间 \(2x\)。之后,新客人填满所有编号为奇数的房间。
现在有 \(q\) 次操作,每次操作为如下三种之一:
-
1 k:若 \(k≥1\),表示有 \(k\) 人到达酒店。若 \(k=0\),则表示有无数人到达酒店。将团队编号 \(G\) 分配给新来宾,然后将 \(G\) 加 \(1\)。 -
2 g x:求团队编号为 \(g\) 的客人中的第 \(x\) 小的房间号。输出其对 \(10^9 + 7\) 取模后的结果。 -
3 x:求 \(x\) 号房间内客人的团队编号。
假设初始时酒店里住满了无数个团队编号为 \(0\) 的客人。
\(q \leq 3 \times 10^5\),\(g < G\),\(x,k \leq 10^9\)。
对于操作 \(2\),我们维护最小值的位置以及公差,每次相当于区间 \(\times 2\) 或区间 \(+k\),用线段树维护即可。
对于操作 \(3\),考虑将修改回溯,那么至多只会有 \(\log\) 个 \(k=0\) 的修改,这些修改将所有修改分成了 \(\log\) 块,只需要记录每块的前缀和,从后往前找到对应的块,然后二分就行了。
总时间复杂度 \(O(q \log V)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 5, M = N << 2, mod = 1e9 + 7;
#define pb push_back
#define mp make_pair
#define ls o << 1
#define rs o << 1 | 1
#define mid ((l + r) >> 1)
#define LS ls, l, mid
#define RS rs, mid + 1, r
void inc(int &x, int y) { x = (x + y >= mod) ? (x + y - mod) : (x + y); }
int pls(int x, int y) { return (x + y >= mod) ? (x + y - mod) : (x + y); }
struct SGT {
int v[M], add[M], mul[M];
void build(int o, int l, int r) {
v[o] = add[o] = 0, mul[o] = 1;
if (l == r) return;
build(LS), build(RS);
}
void up(int o) { v[o] = pls(v[ls], v[rs]); }
void pmul(int o, int k) {
add[o] = 1ll * add[o] * k % mod;
mul[o] = 1ll * mul[o] * k % mod;
v[o] = 1ll * v[o] * k % mod;
}
void padd(int o, int k, int L) {
inc(add[o], k);
inc(v[o], 1ll * k * L % mod);
}
void down(int o, int L) {
if (mul[o] != 1) {
pmul(ls, mul[o]);
pmul(rs, mul[o]);
mul[o] = 1;
}
if (add[o]) {
padd(ls, add[o], L - (L >> 1));
padd(rs, add[o], L >> 1);
add[o] = 0;
}
}
void tadd(int o, int l, int r, int L, int R, int k) {
if (r < L || l > R) return;
if (L <= l && R >= r) return padd(o, k, r - l + 1);
down(o, r - l + 1);
tadd(LS, L, R, k), tadd(RS, L, R, k), up(o);
}
void tmul(int o, int l, int r, int L, int R) {
if (r < L || l > R) return;
if (L <= l && R >= r) return pmul(o, 2);
down(o, r - l + 1);
tmul(LS, L, R), tmul(RS, L, R), up(o);
}
void upd(int o, int l, int r, int p, int k) {
if (l == r) return v[o] = k, void();
down(o, r - l + 1);
(p <= mid ? upd(LS, p, k) : upd(RS, p, k)), up(o);
}
int qry(int o, int l, int r, int p) {
if (l == r) return v[o];
down(o, r - l + 1);
return (p <= mid ? qry(LS, p) : qry(RS, p));
}
} T1, T2;
#undef mid
int n, m, q, stk[N], tp, l[N], lst, fl;
vector <LL> vr[N];
int main() {
scanf("%d", &q), n = 1;
T1.build(1, 1, q), T1.upd(1, 1, q, 1, 0);
T2.build(1, 1, q), T2.upd(1, 1, q, 1, 1);
stk[++tp] = 1;
for (int i = 1, op; i <= q; i++) {
scanf("%d", &op);
if (op == 1) {
int k; scanf("%d", &k);
if (k) {
T1.tadd(1, 1, q, 1, n, k);
n++;
T1.upd(1, 1, q, n, 0);
T2.upd(1, 1, q, n, 1);
if (fl) vr[m].pb(vr[m].back() + k);
else vr[++m].pb(k);
fl = 1, lst = 0;
} else {
T1.tmul(1, 1, q, 1, n);
T2.tmul(1, 1, q, 1, n);
n++;
T1.upd(1, 1, q, n, 1);
T2.upd(1, 1, q, n, 2);
stk[++tp] = n;
fl = 0;
if (!lst) l[tp] = n, lst = n;
else l[tp] = lst;
}
} else if (op == 2) {
int g, x; scanf("%d %d", &g, &x); g++;
int s = T1.qry(1, 1, q, g);
int k = T2.qry(1, 1, q, g);
cout << pls(s, 1ll * k * (x - 1) % mod) << '\n';
} else {
int x; scanf("%d", &x);
int _tp = tp, _m = m, o = fl, cur = n + 1;
while (1) {
if (o) {
if (x >= vr[_m].back()) x -= vr[_m].back(), --_m, o = 0;
else {
int l = 0, r = vr[_m].size() - 1, ans;
LL s = vr[_m].back();
while (l <= r) {
int mid = (l + r) >> 1;
if (s - vr[_m][mid] <= x) r = mid - 1, ans = mid;
else l = mid + 1;
}
ans = cur - (vr[_m].size() - ans);
cout << ans - 1 << '\n';
break;
}
} else {
if (_tp == 1) { puts("0"); break; }
if (x == 0) { cout << max(l[_tp] - 1, 1) - 1 << '\n'; break; }
if (x % 2) { cout << stk[_tp] - 1 << '\n'; break; }
cur = stk[_tp--], x /= 2;
if (stk[_tp] + 1 != stk[_tp + 1]) o = 1;
}
}
}
}
return 0;
}
G. Lexicographically Minimum Walk
给定一个 \(n\) 个点 \(m\) 条边的有向图,边有边权 \(c_i\)。求 \(s\) 到 \(t\) 字典序最小的路径。
\(n \leq 10^5\),\(m \leq 3 \times 10^5\),\(c_i \leq 10^9\)。
首先只保留能到达 \(t\) 的点,如果 \(s\) 不能到达 \(t\) 则无解。
从 \(s\) 开始,每次贪心走 \(c\) 最小的边,如果在到达 \(t\) 之前出现环则会一直沿着环走。否则第一次到达 \(t\) 时的路径就是答案。时间复杂度 \(O(n+m)\)。
code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef pair <int, int> pi;
#define pb push_back
#define fi first
#define se second
int n, m, s, t, vis[N], f[N], a[N];
vector <pi> e[N]; vector <int> g[N], pa;
bool cmp(pi i, pi j) { return i.se < j.se; }
void dfs(int u) {
f[u] = 1;
for (int v : g[u]) if (!f[v]) dfs(v);
}
void get(int u) {
if (vis[u]) { puts("TOO LONG"); exit(0); }
vis[u] = 1;
if (u == t) { for (int z : pa) printf("%d ", z); exit(0); }
for (pi p : e[u]) {
int v = p.fi;
if (f[v]) pa.pb(p.se), get(v);
}
}
int main() {
ios :: sync_with_stdio(0);
cin >> n >> m >> s >> t;
for (int i = 1, u, v, c; i <= m; i++) {
cin >> u >> v >> c;
e[u].pb({v, c}), g[v].pb(u);
}
for (int i = 1; i <= n; i++) sort(e[i].begin(), e[i].end(), cmp);
dfs(t);
if (!f[s]) return puts("IMPOSSIBLE"), 0;
get(s);
return 0;
}
H. Maximizer
给定两个长为 \(n\) 的排列 \(a,b\),每次操作可以选择一个 \(i \in [0,n)\),然后交换 \(a_i,a_{i+1}\)。
求最少需要多少次操作使得 \(\sum \limits_{i=1}^n |a_i - b_i|\) 的值最大。
\(n \leq 2.5 \times 10^5\)。
考虑 \(|a_i - b_i|\) 的实质,这相当于给一对匹配中较大数分配了一个系数 \(1\),较小数分配了一个系数 \(-1\)。我们希望分配到 \(1\) 的系数尽量大,显然 \(\{1,2,\cdots,n\}\) 和 \(\{n,n-1,\cdots,1\}\) 能够取到最大值。
更进一步地:当 \(n\) 为偶数时,取到最大值当且仅当每对 \((a_i,b_i)\) 都由一个 \(\le \frac{n}{2}\) 的数和 \(> \frac{n}{2}\) 的数组成。当 \(n\) 为奇数时取到最大值当且仅当每对 \((a_i,b_i)\) 都由一个 \(\le \frac{n+1}{2}\) 和一个 \(\ge \frac{n+1}{2}\) 的数组成。
相当于我们将 \(a\) 和 \(b\) 分别分成了 \(A_0,A_1\) 和 \(B_0,B_1\),其中 \(A_0\) 和 \(B_1\) 匹配,\(A_1\) 和 \(B_0\) 匹配。显然只要一个部分匹配了另一个部分也自然匹配了。枚举哪个部分匹配,显然最小交换次数就是从小到大排序后对应位置的差的绝对值之和。总时间复杂度 \(O(n)\)。
code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef vector <int> vi;
typedef long long LL;
#define pb push_back
int n, a[N], b[N]; vi va, vb; LL ans, w;
int main() {
ios :: sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
double mid = 1.0 * (n + 1) / 2;
for (int i = 1; i <= n; i++) if (a[i] <= mid) va.pb(i);
for (int i = 1; i <= n; i++) if (b[i] >= mid) vb.pb(i);
for (int i = 0; i < (n + 1) / 2; i++) ans += abs(va[i] - vb[i]);
va.clear(), vb.clear();
for (int i = 1; i <= n; i++) if (a[i] >= mid) va.pb(i);
for (int i = 1; i <= n; i++) if (b[i] <= mid) vb.pb(i);
for (int i = 0; i < (n + 1) / 2; i++) w += abs(va[i] - vb[i]);
cout << min(ans, w) << endl;
return 0;
}
I. Minimum Diameter Spanning Tree
给定一个 \(n\) 个点 \(m\) 条边的无向图,求其最小直径生成树。
\(n \leq 500\),\(m \leq \frac{n \times (n-1)}{2}\),时限 \(\text{5.0s}\)。
考虑先求出图的绝对中心,求出绝对中心后,从绝对中心开始生成一个最短路径树即为答案。
设 \(d(i,j)\) 为 \(i,j\) 之间的最短路径长度。考虑枚举每条边 \((u,v)\),设其长为 \(L\),并假设绝对中心 \(p\) 在这条边上并且距离 \(u\) 长为 \(x(x \le L)\)。那么对于图中任意一点 \(i\),\(p\) 到 \(i\) 的距离可以写作 \(d(p, i) = \min\{ d(u, i) + x,\ d(v, i) + (L - x) \}\)。
可以看出,\(d(p, i)\) 的函数图像是一个由两条斜率相同的线段构成的折线段。于是 \(p\) 到最远点距离的函数可以写作 \(f = \max\limits_{1\le i\le n}\{d(p, i)\}\),图像是由一堆折线组成的更加曲折的折线。
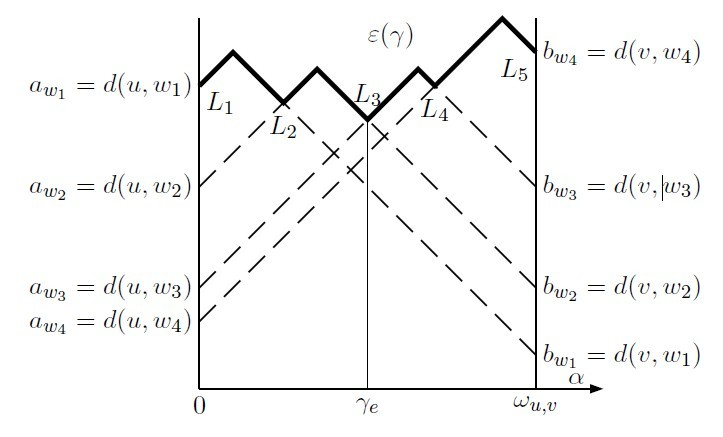
图中的 \(\alpha\) 即为文中的 \(x\),\(\omega_{u, v}\) 即为 \(L\),\(w_{1,\cdots,n}\) 为图中异于 \(u, v\) 的点。答案即为图像中的最低点,横坐标即为绝对中心的位置。接下来考虑如何求出最低点的位置。
显然,最低点是某两条折线的交点。对于图中的两点 \(i, j\),若 \(d(u, i) \ge d(u, j)\) 且 \(d(v, i) \ge d(v, j)\),那么 \(d(p, j)\) 的函数图像完全位于 \(d(p, i)\) 下方,因此我们可以直接将折线 \(j\) 删掉。
对于剩下的折线,若我们将它们按照 \(d(u, i)\) 从大到小排序,那么对应 \(d(v, i)\) 的大小是递减的,于是排序后相邻两折线必定会有交点,并且最低点一定在这些交点之中,依次检查即可。时间复杂度 \(O(n^3 + nm)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef vector <int> vi;
typedef pair <int, int> pi;
#define pb push_back
#define mp make_pair
const int N = 5e2 + 5;
const LL inf = 1e18;
struct E {
int u, v; LL w;
} e[N * N];
int n, m, pre[N], rk[N][N];
LL d[N][N], g[N][N], tmp[N], ans, dis[N], X;
bool cmp(int i, int j) { return tmp[i] < tmp[j]; }
vi adj[N];
set <pi, less<pi> > q, res;
void dij(int s1, int s2) {
for (int i = 1; i <= n; i++) dis[i] = inf;
dis[s1] = X, dis[s2] = g[s1][s2] - X;
q.insert(mp(dis[s1], s1));
q.insert(mp(dis[s2], s2));
if (s1 != s2) pre[s2] = s1;
while (!q.empty()) {
auto it = q.begin();
int u = it -> second;
q.erase(*it);
for (int v : adj[u]) if (dis[v] > dis[u] + g[u][v]) {
q.erase(mp(dis[v], v));
dis[v] = dis[u] + g[u][v];
q.insert(mp(dis[v], v));
res.erase(mp(pre[v], v));
pre[v] = u;
res.insert(mp(pre[v], v));
}
}
}
int main() {
ios :: sync_with_stdio(0);
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = inf;
for (int i = 1; i <= n; i++)
d[i][i] = 0;
for (int i = 1, u, v, w; i <= m; i++) {
cin >> u >> v >> w; w *= 2;
e[i].u = u, e[i].v = v, e[i].w = g[u][v] = g[v][u] = w;
d[u][v] = d[v][u] = w;
adj[u].pb(v), adj[v].pb(u);
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
rk[i][j] = j;
tmp[j] = d[i][j];
}
sort(rk[i] + 1, rk[i] + n + 1, cmp);
}
ans = inf; int s1, s2;
for (int k = 1; k <= m; k++) {
int u = e[k].u, v = e[k].v;
if (d[u][rk[u][n]] == d[u][rk[u][n - 1]] && d[u][rk[u][n]] * 2ll < ans) {
ans = d[u][rk[u][n]] * 2ll;
s1 = u;
s2 = u;
}
if (d[v][rk[v][n]] == d[v][rk[v][n - 1]] && d[v][rk[v][n]] * 2ll < ans) {
ans = d[v][rk[v][n]] * 2ll;
s1 = v;
s2 = v;
}
int lst, cur;
for (cur = n - 1, lst = n; cur >= 1; cur--) {
if (d[v][rk[u][lst]] < d[v][rk[u][cur]]) {
if (d[u][rk[u][cur]] + d[v][rk[u][lst]] + e[k].w < ans) {
ans = d[u][rk[u][cur]] + d[v][rk[u][lst]] + e[k].w;
X = ans / 2 - d[u][rk[u][cur]];
s1 = u;
s2 = v;
}
lst = cur;
}
}
}
cout << ans / 2ll << endl;
dij(s1, s2);
for (auto [x, y] : res)
cout << x << " " << y << "\n";
if (s1 != s2)
cout << s1 << " " << s2 << "\n";
return 0;
}
J. Parklife
给定 \(n\) 条线段,第 \(i\) 条线段 \([l_i,r_i]\) 有权值 \(c_i\)。
现在你需要选择其中的一些线段,使得每个位置被不超过 \(k\) 条线段覆盖,并最大化这些线段的权值和。你只需要求出这个最大的权值。对 \(k = i \in [1,n]\) 求出答案。
\(n \leq 2.5 \times 10^5\),\(l_i < r_i \leq 10^6\),\(c_i \leq 10^9\)。
显然这些线段的结构是一颗树,我们不妨就建出这颗树。
考虑 DP,设 \(f_{u,i}\) 表示 \(u\) 的子树内最多覆盖 \(i\) 层的最大权值。DP 的转移是简单的:将所有儿子的 \(f\) 相加,并与 \([0,w_u]\) 卷积。由此容易归纳证明 \(f_u\) 是一个凸函数。
于是 \(f_u\) 的差分数组单调递增。考虑用小根堆维护 \(f\) 的差分,求 \(\sum f_v\) 是简单的,与 \([0,w_u]\) 卷积相当于向差分数组中插入了一个 \(w_u\),时间复杂度 \(O(n \log n)\)。
code
#include <bits/stdc++.h>
using namespace std;
const int N = 2.5e5 + 5;
typedef long long LL;
typedef vector <int> vi;
#define pb push_back
int n, stk[N], tp; vi e[N];
struct dat {
int l, r; LL w;
} a[N];
bool cmp(const dat &i, const dat &j) {
return (i.l != j.l) ? (i.l < j.l) : (i.r > j.r);
}
priority_queue <LL> q[N];
void dfs(int u, int ff) {
for (int v : e[u]) {
if (v == ff) continue;
dfs(v, u);
if (q[u].empty()) swap(q[u], q[v]);
else {
vector <LL> f;
if (q[u].size() < q[v].size()) swap(q[u], q[v]);
while (!q[v].empty()) {
LL a = q[u].top;
LL b = q[v].top;
f.pb(a + b);
q[u].pop();
q[v].pop();
}
for (LL x : f) q[u].push(x);
}
}
q[u].push(a[u].w);
}
int main() {
ios :: sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].l >> a[i].r >> a[i].w;
}
++n, a[n].l = 1, a[n].r = 1e6, a[n].w = 0;
sort(a + 1, a + n + 1, cmp);
stk[++tp] = 1;
for (int i = 2, f; i <= n; i++) {
f = stk[tp];
while (a[i].r > a[f].r) f = stk[--tp];
e[f].pb(i);
e[i].pb(f);
stk[++tp] = i;
}
dfs(1, 0); LL ans = 0;
for (int i = 1; i < n; i++) {
if (!q[1].empty()) {
ans += q[1].top(), q[1].pop();
}
cout << ans << " ";
}
cout << "\n";
return 0;
}
K. Wind of Change
给定两颗 \(n\) 个点的树 \(T_1,T_2\),边有边权。
定义 \(d(T_1,i,j)\) 为 \(i,j\) 在 \(T_1\) 上的距离,\(d(T_2,i,j)\) 同理。对每个点 \(i\) 求出 \(\min \limits_{j \neq i} \{ d(T_1,i,j) + d(T_2,i,j) \}\)。
\(n \leq 2.5 \times 10^5\),\(w_i \leq 10^9\),时限 \(\text{12.0s}\)。
本题做法多种多样,这里给一种看起来比较麻烦的(
对第一颗树边分治,求出每个点的边分树,然后对第二颗树边分治,那么问题就变成了给定两个集合,要查询每个点到另一个集合内点的答案,我们把两个集合内所有点的边分树分别合并,这样每次查询就是 \(\log\) 的了。
时间复杂度 \(O(n \log^2 n)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef vector <int> vi;
typedef long long LL;
const int N = 1e6 + 5, M = N << 1, S = 5e7 + 5;
const LL inf = 1e18;
#define pb push_back
void chkmin(LL &x, LL y) { x = min(x, y); }
int n;
namespace T1 {
int rt[N], ls[S], rs[S], all; LL tr[S], dis[N], ans[N];
void ins(int x, int y) {
int cur = rt[x];
while (1) {
if (ls[cur]) {
if (!ls[y]) ls[y] = ++all, tr[all] = inf;
chkmin(tr[ls[y]], tr[ls[cur]] + dis[x]);
cur = ls[cur], y = ls[y];
} else if (rs[cur]) {
if (!rs[y]) rs[y] = ++all, tr[all] = inf;
chkmin(tr[rs[y]], tr[rs[cur]] + dis[x]);
cur = rs[cur], y = rs[y];
} else break;
}
}
void del() {
tr[all] = inf, ls[all] = rs[all] = 0, all--;
}
LL qry(int x, int y) {
int cur = rt[x]; LL res = inf;
while (1) {
if (ls[cur]) {
chkmin(res, tr[ls[cur]] + dis[x] + tr[rs[y]]);
cur = ls[cur], y = ls[y];
} else if (rs[cur]) {
chkmin(res, tr[rs[cur]] + dis[x] + tr[ls[y]]);
cur = rs[cur], y = rs[y];
} else break;
}
return res;
}
void calc(vi &L, vi &R) {
int tmp = all, l = ++all, r = ++all;
for (int x : L) ins(x, l);
for (int x : R) ins(x, r);
for (int x : L) chkmin(ans[x], qry(x, r));
for (int x : R) chkmin(ans[x], qry(x, l));
while (all > tmp) del();
}
int m, to[M], nxt[M], hd[N], cnt, val[M];
void add(int u, int v, int w) {
to[++cnt] = v, nxt[cnt] = hd[u], hd[u] = cnt, val[cnt] = w;
}
vi son[N]; int h[N];
void dfs0(int u, int ff) {
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (v == ff) continue;
dfs0(v, u), h[v] = val[i], son[u].pb(v);
}
}
void build() {
dfs0(1, 1), cnt = 1, m = n;
for (int i = 1; i <= n; i++) hd[i] = 0;
for (int i = 1; i <= n; i++) ans[i] = inf;
for (int u = 1; u <= m; u++) {
if (son[u].size() < 3) {
for (int v : son[u]) add(u, v, h[v]), add(v, u, h[v]);
} else {
int L = ++m, R = ++m;
add(u, L, 0), add(L, u, 0);
add(u, R, 0), add(R, u, 0);
for (int v : son[u]) son[L].pb(v), swap(L, R);
}
}
}
int sz[N], mx[N], _rt; bool vis[M];
void find(int u, int ff, int tot) {
sz[u] = 1;
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (vis[i] || v == ff) continue;
find(v, u, tot), sz[u] += sz[v];
mx[i >> 1] = max(tot - sz[v], sz[v]);
if (mx[i >> 1] < mx[_rt]) _rt = (i >> 1);
}
}
vi vr;
void dfs(int u, int ff) {
sz[u] = 1;
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (vis[i] || v == ff) continue;
dis[v] = dis[u] + val[i], dfs(v, u), sz[u] += sz[v];
}
if (u <= n) vr.pb(u);
}
void solve(int u, int tot) {
mx[_rt = 0] = m, find(u, u, tot);
if (!_rt) return;
vis[_rt << 1] = vis[_rt << 1 | 1] = 1;
int L = to[_rt << 1], R = to[_rt << 1 | 1];
vr.clear();
dis[L] = 0, dfs(L, R);
vi vl; swap(vl, vr);
vr.clear();
dis[R] = val[_rt << 1 | 1], dfs(R, L);
calc(vl, vr);
solve(L, sz[L]), solve(R, sz[R]);
}
void work() {
tr[0] = inf;
for (int i = 1, u, v, w; i < n; i++) {
cin >> u >> v >> w;
add(u, v, w), add(v, u, w);
}
build(), solve(1, m);
for (int i = 1; i <= n; i++) cout << ans[i] << '\n';
}
}
namespace T2 {
int m, to[M], nxt[M], hd[N], cnt, val[M];
void add(int u, int v, int w) {
to[++cnt] = v, nxt[cnt] = hd[u], hd[u] = cnt, val[cnt] = w;
}
vi son[M]; int h[M], lst[N];
void dfs0(int u, int ff) {
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (v == ff) continue;
dfs0(v, u), h[v] = val[i], son[u].pb(v);
}
}
void build() {
dfs0(1, 1), cnt = 1, m = n;
for (int i = 1; i <= n; i++) hd[i] = 0;
for (int i = 1; i <= n; i++) T1 :: rt[i] = lst[i] = ++T1 :: all;
for (int u = 1; u <= m; u++) {
if (son[u].size() < 3) {
for (int v : son[u]) add(u, v, h[v]), add(v, u, h[v]);
} else {
int L = ++m, R = ++m;
add(u, L, 0), add(L, u, 0);
add(u, R, 0), add(R, u, 0);
for (int v : son[u]) son[L].pb(v), swap(L, R);
}
}
}
int sz[N], mx[N], rt; bool vis[M];
void find(int u, int ff, int tot) {
sz[u] = 1;
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (vis[i] || v == ff) continue;
find(v, u, tot), sz[u] += sz[v];
mx[i >> 1] = max(tot - sz[v], sz[v]);
if (mx[i >> 1] < mx[rt]) rt = (i >> 1);
}
}
LL dis[N]; vi vr;
void dfs(int u, int ff) {
sz[u] = 1;
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if (vis[i] || v == ff) continue;
dis[v] = dis[u] + val[i], dfs(v, u), sz[u] += sz[v];
}
if (u <= n) vr.pb(u);
}
void solve(int u, int tot) {
mx[rt = 0] = m, find(u, u, tot);
if (!rt) return;
vis[rt << 1] = vis[rt << 1 | 1] = 1;
int L = to[rt << 1], R = to[rt << 1 | 1];
vr.clear();
dis[L] = 0, dfs(L, R);
for (int x : vr) {
T1 :: ls[lst[x]] = ++T1 :: all, lst[x] = T1 :: all;
T1 :: tr[lst[x]] = dis[x];
}
vr.clear();
dis[R] = val[rt << 1], dfs(R, L);
for (int x : vr) {
T1 :: rs[lst[x]] = ++T1 :: all, lst[x] = T1 :: all;
T1 :: tr[lst[x]] = dis[x];
}
solve(L, sz[L]), solve(R, sz[R]);
}
void work() {
for (int i = 1, u, v, w; i < n; i++) {
cin >> u >> v >> w;
add(u, v, w), add(v, u, w);
}
build(), solve(1, m);
}
}
int main() {
ios :: sync_with_stdio(0);
cin >> n;
T2 :: work(), T1 :: work();
return 0;
}

