[学习笔记] 根号数据结构

前几天太摸了，来个大的。参考了 lxl 的 ppt 和神仙们的众多博客。

若没有特殊说明，默认 $n=m={10}^5$。

本文未完。

根号分治

就是在预处理与询问的复杂度之间寻找平衡的一个思想。通常以根号作为问题规模的分界线，规模小于根号的询问可以 $n\sqrt{n}$ 求出，而回答一次规模为 $B\ge n$ 的询问的时间只需要 $\frac{n}{B}\le \sqrt{n}$，那么整个题目就可以做到 $n\sqrt{n}$。

一个简单的抽象是有 $n$ 个和为 $m$ 的数，那么大于 $\frac{m}{B}$ 的数最多只有 $B$ 个。这里的 $B$ 通常取 $\sqrt{n}$。

还有一种常用的技巧是先搞两个暴力出来，然后取个阈值把两个暴力拼一拼，有很大概率能行。

虽然这里说得很简单，但根号分治是一个非常重要的思想，同时也是很厉害的东西，平时做题/考试的时候千万不要把它忘了。

听说 ntf 说过 “没事的时候考虑根号分治”，其实是非常有道理的。

P5901 [IOI2009] regions

容易想到两种暴力：

暴力 $1$：对于询问 $(r1,r2)$，它的答案可以通过 DFS 到一个属性为 $r_1$ 的点时，计算这个点的子树中属性为 $r_2$ 的点的数量求和。

暴力 $2$：对于询问 $(r1,r2)$，它的答案也可以通过 DFS 到一个属性为 $r_2$ 的点时统计 $1\to e_2$ 的路径上有多少属性为 $r_1$ 的点求和。

显然这两个暴力都是不能通过的。考虑把这两个暴力拼一拼，设属性为 $r_2$ 的点数为 $S$，按 $S$ 的大小分别处理：

• 当 $S\ge \sqrt{n}$ 时，最多存在 $\sqrt{n}$ 个这样的 $r2$，那么使用第一种暴力，每个点最多枚举 $\sqrt{n}$ 次，因此复杂度为 $O(n\sqrt{n})$。

• 当 $S\le \sqrt{n}$ 时，每种 $r_2$ 最多出现 $\sqrt{n}$ 次，使用第二种暴力，最多会有 $q\sqrt{n}$ 个询问，复杂度 $O(n\sqrt{n})$。

因此总时间复杂度为 $O(n\sqrt{n})$。

CF1039D You Are Given a Tree

注意到若 $k>\sqrt{n}$，那么答案一定不大于 $\sqrt{n}$。对于 $k\le \sqrt{n}$，我们直接暴力树形 DP。对于 $k>\sqrt{n}$ 的部分，我们枚举答案，显然答案单调不增，二分出答案的区间即可。树形 DP 的部分类似赛道修建，转移比较简单，这里就不说了。

卡常小技巧：将每个节点的父亲预处理出来，然后按照 DFS 序排序，这样可以直接循环树形 DP，就不需要 DFS了。时间复杂度 $O(n\sqrt{n}\log n)$。

分块

分块可以分为动态分块和静态分块两种。

静态分块指的是放一些关键点，预处理关键点到关键点的信息来加速查询，不能支持修改。动态分块指的是把序列分为一些块，每块维护一些信息，可以支持修改。目前认为：如果可以离线，静态分块是莫队算法的子集。

动态分块

以下提到的分块均默认为动态分块。

例题 $1$

维护一个序列，支持区间加，查询区间和。

朴素做法有 $O(n)$ 修改 $O(1)$ 查询和 $O(1)$ 修改 $O(n)$ 查询两种暴力。但我们可以利用根号平衡达到 $O(\sqrt{n})$ 修改 $O(\sqrt{n})$ 查询的复杂度。具体来说，我们可以把原序列分成 $O(\sqrt{n})$ 个块，每个块中有 $O(\sqrt{n})$ 个元素。形态如下图：

我们把每次操作完整覆盖的块称为为“整块”，把每次操作没有完整覆盖的块称为“散块”。从上图中可以看出，每次操作我们最多经过 $O(\sqrt{n})$ 个整块和 $2$ 个散块，所以我们可以 $O(1)$ 维护整块信息，$O(\sqrt{n})$ 查询散块信息，这样就达到了 $O(m\sqrt{n})$ 的复杂度。

事实上，分块的结构是一个度数为 $O(\sqrt{n})$，但只有三层的树。每次修改只需要分别更新 $O(\sqrt{n})$ 个二层节点和 $O(\sqrt{n})$ 个叶子节点，并且我们不用维护根节点的信息。因为树的形态相对简单，因此实际应用时我们一般不会显式地建出树的结构。

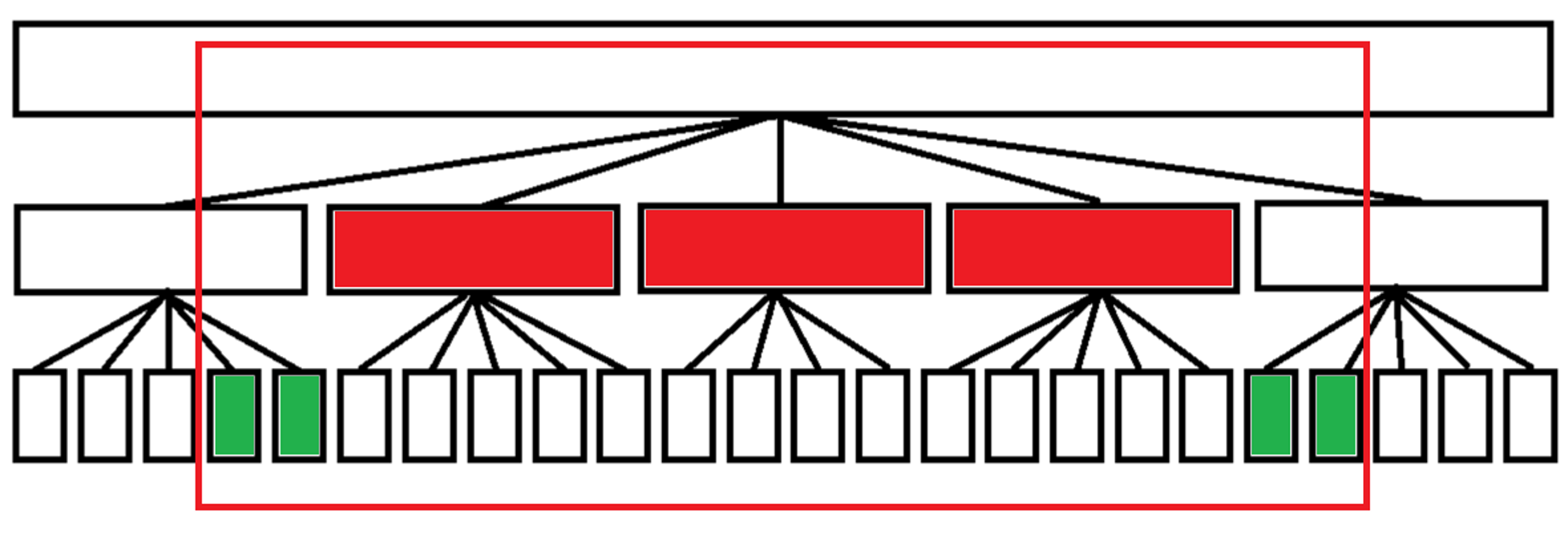
所以如果在分治结构上很难快速合并某些信息，我们就可以考虑利用分块来做。

例题 $2$

维护一个序列，支持区间加，查询区间小于 $x$ 的数的个数。

容易发现，区间加这个操作使得我们没有办法在分治结构上快速地合并信息。考虑分块，维护每个块内排序后的数组。每次区间加时，对整块打标记，散块可以重构。查询时，假设整块查询小于 $x$ 的数，这个整块的标记为 $y$，那么等价于查询整块排序后的数组中小于 $x-y$ 的数的个数，这可以二分解决。对于零散快，我们直接暴力查询即可。

分析一下复杂度，假设分成了 $x$ 个块，查询时，整块复杂度 $O(x\log \frac{n}{x})$，散块复杂度 $O(\frac{n}{x})$。修改时，整块复杂度 $O(1)$，散块复杂度 $O(\frac{n}{x})$（重构时使用归并）。简单计算可得当 $x=\sqrt{n\log n}$ 时取最优复杂度 $O(m\sqrt{n\log n})$。

根号平衡

有时，根据修改和查询次数的不同，我们需要调整每次修改和查询的复杂度，使得整体复杂度得到平衡。以下举几个简单例子：

• $O(1)$ 单点修改，$O(\sqrt{n})$ 区间和：分块维护块内和，每次修改更新块内和以及该位置在数组上的值，查询和普通分块一样。

• $O(\sqrt{n})$ 单点修改，$O(1)$ 区间和：分块维护整块前缀和和每个块内前缀和，查询时把前缀和拼起来即可。

• $O(1)$ 区间加，$O(\sqrt{n})$ 查单点：每次区间加时差分成两个前缀加减，同时在数组和块上打标记，查询时扫一遍块内标记和块外标记即可。

• $O(\sqrt{n})$ 区间加，$O(1)$ 查单点：直接分块即可。

• $O(1)$ 往集合中加入一个数，$O(\sqrt{n})$ 查询 $k$ 小（值域 $O(n)$）：离散化后对值域分块，每次查询从左往右扫，最多经过 $\sqrt{n}$ 个整块和 $\sqrt{n}$ 个单点。

• $O(\sqrt{n})$ 往集合中加入一个数，$O(1)$ 查询 $k$ 小（值域 $O(n)$）：对值域分块，对每个数维护其在哪个块中，对每个块维护一个从小到大的有序表表示块内的数，修改的时候只会改变 $O(\sqrt{n})$ 个数所属的块，查询的时候定位其所属的块，然后找到在该块中对应位置的值即可。

Chef and Churu

先对函数分块，维护整块的答案，这只需要差分+前缀和预处理出每个数在块内出现的次数，修改是简单的。但查询时，我们希望对于散块能够 $O(1)$ 查询每个区间的和。再次根号平衡，我们对序列分块，维护整块前缀和和块内前缀和即可 $O(\sqrt{n})$ 修改 $O(1)$ 查询。设块大小为 $B$，总时间复杂度为 $O(\frac{n^2}{B}+q(B+\frac{n}{B}))$，当 $B=\sqrt{n}$ 时取最优复杂度 $O((n+q)\sqrt{n})$。

P3863 序列

将询问离线，扫描线扫序列维，数据结构维护时间维，然后变成区间加区间排名，分块维护即可。

静态分块

静态分块一般通过预处理一些信息来得到更好的复杂度，通常分整块和散块的几种情况来考虑。它的功能是莫队的子集，因此一般对于强制在线的问题我们才考虑使用静态分块。

P4168 [Violet]蒲公英

考虑分块，设块数为 $B$，如果询问区间在同一块直接暴力，否则每次询问的众数要么是整块中的众数，要么是某个散块中出现过的数。整块的答案可以预处理 $f_{i,j}$ 表示第 $i$ 块到第 $j$ 块内的众数，散块的答案可以预处理 $s_{i,j}$ 表示前 $i$ 块中 $a_j$ 出现的次数，暴力差分查询即可。

预处理 $s,f$ 复杂度均为 $O(\frac{n^2}{B})$，暴力 $O(B)$，查询整块答案 $O(1)$，查询散块答案 $\frac{n}{B}$，取 $B=\sqrt{n}$ 得最优时间复杂度 $O(n\sqrt{n})$。

P5046 [Ynoi2019 模拟赛] Yuno loves sqrt technology I

考虑分块，设块数为 $B$，当询问在同一块时可以预处理出 $p_{i,j}$ 表示 $i$ 往后 $j$ 个数中有多少个数小于 $a_i$，则答案为 $\sum p_{i,r-i}$。容易发现 $j\le B$，分块预处理即可。具体来说可以类似差分，先用数据结构预处理出每个数右边块内比它小的数的个数 $c_i$，然后从后往前扫，在 $i$ 加入数据结构后更新 $j\le i$ 的 $p_j$。预处理 $f$ 的时间复杂度为 $O(\frac{n^2}{B})$，回答询问的复杂度为 $O(\frac{n}{B})$。

如果询问不在同一块，我们分几种情况分别考虑：

• 散块及整块内部：预处理每块的前缀答案和后缀答案即可。

• 散块间：$O(\frac{n}{B})$ 归并计算即可。

• 散块到整块：设 $f_{i,j}$ 为第 $j$ 块中小于 $a_i$ 的数的个数，这可以 $O(nB)$ 预处理。答案即 $\sum _{be{l}_i=be{l}_l}\sum _{be{l}_l<j<be{l}_r}{f}_{i,j}+\sum _{be{l}_i=be{l}_r}\sum _{be{l}_l<j<be{l}_r}{f}_{i,j}$，可以 $O(nB)$ 前缀和算出 $s_{i,j}=\sum _{k\le j}{f}_{i,j}$ 然后 $O(\frac{n}{B})$ 计算。

• 整块到整块：即 $\sum _{be{l}_l<k<be{l}_r}\sum _{be{l}_i=k}\sum _{k<j<be{l}_r}{f}_{i,j}$，即 $\sum _{be{l}_l<k<be{l}_r}\sum _{be{l}_i=k}{s}_{i,be{l}_r-1}-s_{i,k}$，$O(nB)$ 预处理 $g_{i,j}=\sum _{be{l}_k=i}{s}_{k,j}$ 后答案即为 $\sum _{be{l}_l<k<be{l}_r}{g}_{k,be{l}_r-1}-g_{k,k}$，可以 $O(B)$ 计算。

取 $B=\sqrt{n}$，预处理复杂度均为 $O(n\sqrt{n})$，求答案复杂度为 $O(n)$，因此总时间复杂度为 $O(n\sqrt{n})$。实现时可能需要调整一些数组的维度顺序来减少 cache miss。

操作分块

本质是对时间轴分块。

P5443 [APIO2019] 桥梁

如果只有操作 $2$，将边按照 $w$ 从大到小加入边即可，但这个做法不能支持边权修改。

考虑操作分块，设把操作分为 $B$ 块，对于每一个块，如果没有修改，那么可以按照没有修改的方式做。如果有修改，我们先不加入被修改的边，而是把所有被修改的边积一起处理。具体来说，我们扫一遍时间小于当前询问的块内的修改，把边的权值改掉，然后把修改后依然合法的边加进去。对于修改时间在当前询问之后的修改我们直接以原本的权值加入即可。询问后需要把修改的边集体删除，需要支持可撤销并查集。这部分时间复杂度为 $O(\frac{m}{B}\log n)$。

每条边最多被加进 $B$ 个块，复杂度为 $O(Bm\log n)$。对于块内，被修改的边最多有 $O(\frac{m}{B})$ 个，因此所有块的修改撤回复杂度为 $O(\frac{m^2}{B}\log n)$。因此总复杂度为 $O(Bm\log n+\frac{m^2}{B}\log n)$，取 $B=\sqrt{m}$ 得最优复杂度 $O(m\sqrt{m}\log n)$。

CF1588F Jumping Through the Array

如果直接暴力修改并进行加操作，这样单次复杂度 $O(n)$。考虑进行优化。

对于 $2$ 操作，每一个环长都是 $O(n)$ 级别的，我们考虑进行操作分块，设将 $B$ 个操作分成一块，我们发现对于每一个需要修改的位置，从它到它后边第一个需要修改位置之前的所有位置的 $p$ 都不会发生变化，所以我们可以将这些位置缩成一个，这样环长就是 $O(B)$ 级别了，每次可以暴力遍历。而每次预处理要花 $O(\frac{q}{B}\times n)$ 的时间缩点。

对于 $1$ 操作，我们直接查询每一个需要修改的位置所带来的贡献。我们可以记录所有要修改位置所对应的缩后的点一共包含了多少 $1$ 到 $i$ 的点，然后从左往右扫一遍，假如遇到了一个之后需要查询的位置，我们就将这些信息记录下来，这样在询问时可以直接差分得到询问的区间里有多少个要修改的点，这样预处理复杂度 $O(B^2)$，单次查询复杂度 $O(B)$。

总复杂度为 $O(\frac{q}{B}\times (n+B^2)+qB)$，取 $B=\sqrt{n}$ 得最优复杂度 $O(q\sqrt{n})$。

莫队

能够高效维护区间信息的一种算法。假设有 $2$ 个区间询问 $[l_1,r_1]$ 和 $[l_2,r_2]$，如果我们可以 $O(x)$ 加入或删除一个元素，即当我们得到了 $[l,r]$ 的答案时我们可以在 $O(x)$ 的复杂度内得到 $[l+1,r],[l-1,r],[l,r+1],[l,r-1]$ 的答案，那么我们我们可以在 $O(x(|l_1-l_2|+|r_1-r_2|))$ 的时间内由 $[l_1,r_1]$ 的答案得到 $[l_2,r_2]$ 的答案。

对于序列长为 $n$，有 $m$ 个询问的情况，我们考虑以一种特殊的顺序依次处理每个询问使得 $\sum (|l_i-l_{i-1}|+|r_i-r_{i-1}|)$ 在一个可以接受的范围内。对序列以每块大小 $\frac{n}{\sqrt{m}}$ 分块，然后把询问排序，排序的时候以左端点所在块编号为第一关键字，右端点位置为第二关键字，可以证明这样做的复杂度是 $O(n\sqrt{m})$ 的。

一个基础的卡常方法是奇偶排序，即对于奇数块右端点从小到大排，右端点从大到小排。原理很简单，奇数块右端点会到右边去，偶数块右端点回来的时候就可以顺便处理掉询问了。

P4689 [Ynoi2016] 这是我自己的发明

容易发现换根是假的，根据 DFS 序转化成区间查询，每个点对应 $1\sim 2$ 个 DFS 序上的区间。 $2$ 个区间不好维护，我们可以考虑差分，这样都能变成前缀的询问。但是在在最坏的情况下我们需要拆出 $4\times 4=16$ 个询问，无法通过本题。但发现 $f_{1,i,1,n}$ 是可以预处理的，这样每次查询只用拆出 $4$ 个询问，具体留给读者一一验证。然后跑莫队就行了。

P3604 美好的每一天

能够重排成回文串的条件：区间内至多只有一个数出现奇数次。容易想到异或，每一位代表一种字符出现次数的奇偶性，维护前缀异或值 $b_i$ 后区间 $[l,r]$ 的异或和相当于 $b_{l-1}\oplus b_r$。于是问题变成了查询有多少二元组 $(i,j)$ 满足 $b_{i-1}\oplus b_j=2^k(0\le k<26)$。莫队维护即可，转移直接枚举每一位算算贡献。设字符集大小为 $c$，则时间复杂度为 $O(nc\sqrt{n})$。

莫队二次离线

莫队二次离线基于莫队 + 扫描线的思想，通过扫描线，再次将更新答案的过程离线处理，以降低时间复杂度。具体地，若更新答案的复杂度为 $O(k)$，那么它可以将莫队的复杂度从 $O(nk\sqrt{n})$ 降到 $O(nk+n\sqrt{n})$。

其本质是将莫队当做 $O(n\sqrt{m})$ 次查询区间内满足某特定特征的元素的某个信息，如果这个信息具有可减性，那么可以差分，差分后就变成 $O(n\sqrt{m})$ 次查询前缀满足某特定特征的元素的某个信息，这样插入次数 $O(n)$，查询次数 $O(n\sqrt{m})$。

由于只进行了 $O(n)$ 次插入，所以我们可以考虑把根号平衡向插入的方向移动，插入代价可以较高，从而降低查询代价。

P4887 【模板】莫队二次离线（第十四分块(前体)）

如果使用用普通莫队，每一次移动指针的复杂度为 $O(C_{14}^k)$，显然过不去。考虑莫队二次离线，设 $a_x$ 对 $[l,r]$ 的贡献为 $f(x,[l,r])$，我们考虑区间端点变化对答案的影响，以 $[l,r]\to [l,r+k]$ 为例，答案增加了 $\sum _{i=r+1}^{r+k}f(i,[l,i-1])$。

注意到，$f(i,[l,i-1])$ 可以差分成 $f(i,[1,i-1])-f(i,[1,l-1])$，这样转移的贡献分为两类：

1. 一个前缀和它后面一个数的贡献，这可以预处理。
2. 区间 $[r+1,r+k]$ 对 $[1,l-1]$ 的贡献，离线后扫描线即可。

对于其他情况也是类似的，四种情况对应的贡献变化如下：

• $[l,r]\to [l,r+k]$，答案增加 $\sum _{i=r+1}^{r+k}f(i,[1,i-1])-f(i,[1,l-1])$。
• $[l,r]\to [l,r-k]$，答案减少 $\sum _{i=r-k+1}^{r}f(i,[1,i-1])-f(i,[1,l-1])$。
• $[l,r]\to [l+k,r]$，答案减少 $\sum _{i=l}^{l+k-1}f(i,[1,r])-f(i,[1,i])$。
• $[l,r]\to [l-k,r]$，答案增加 $\sum _{i=l-k}^{l-1}f(i,[1,r])-f(i,[1,i])$。

对于扫描线部分，对每个前缀开一个 vector 存二元组 $(l_0,r_0)$（对应上面的 $[r+1,r+k]$），算算贡献即可。莫队部分时间复杂度 $O(n\sqrt{n})$（也可以利用前缀和优化至 $O(n)$，但这是无关紧要的），扫描线部分时间复杂度为 $O(n\sqrt{n}+n{C}_{14}^k)$，因此总时间复杂度为 $O(n\sqrt{n}+n{C}_{14}^k)$。

P5047 [Ynoi2019 模拟赛] Yuno loves sqrt technology II

空间限制 $O(n)$。

首先 $O(n\sqrt{n}\log n)$ 谁都会做，而且谁都知道被卡了。于是我们考虑莫队二次离线，对于第一类贡献，预处理即可。对于第二类贡献，左端点移动答案变化量为比这个数小的数的个数，右端点移动答案变化量为比这个数大的数的个数。

对于第二类贡献如果使用树状数组 $O(\log n)$ 修改 $O(\log n)$ 查询，时间复杂度为 $O(n\log n+n\sqrt{n}\log n)$，甚至不如被卡的算法。但由于我们只有 $O(n)$ 次插入，于是我们考虑将复杂度向修改的方向平衡。值域分块维护前缀和即可做到 $O(\sqrt{n})$ 修改 $O(1)$ 查询，这样时间复杂度为 $O(n\sqrt{n})$，然后就做完了。

带修莫队

带修莫队是一种支持单点修改的莫队算法。

如果没有修改操作，一次询问可以表示为二元组 $(l,r)$，加上修改操作之后，一次询问可以表示为 $(l,r,t)$，$t$ 表示在查询 $[l,r]$ 之前做了 $t$ 次修改操作。也可以把 $t$ 理解成时间，显然有 $1\le t\le m$，$m$ 是操作次数。和普通莫队类似，我们先以左端点所在块为第一关键字，以右端点所在块为第二关键字，以时间为第三关键字对询问排序。

暴力查询时，如果当前修改数比询问的修改数少就把没修改的进行修改，反之回退。

需要注意的是，修改分为两部分：

1. 若修改的位置在当前区间内，需要更新答案。

2. 无论修改的位置是否在当前区间内，都要进行修改。

分块大小的选择及复杂度证明

以下用 $B$ 表示分块大小，$c$ 表示修改个数，$q$ 表示询问个数，l 块表示 $\frac{l}{B}$ 分的块，r 块表示 $\frac{r}{B}$ 分的块，每个 l 块包含 $\frac{n}{B}$ 个 r 块。对三个指针分别分析：

1. 对时间指针：对每个 r 块最坏情况下会移动 $c$，共有 $(\frac{n}{B}{)}^2$ 个 r 块，所以总移动次数为 $O(\frac{c{n}^2}{B^2})$。

2. 对左端点指针：l 块内移动每次最多 $B$，换 l 块每次最多 $2B$，所以从移动次数为 $O(qB)$。

3. 对右端点指针：r 块内移动每次最多 $B$，换 r 块每次最多 $2B$，所以在 l 块内移动次数之和为 $O(qB)$。换 l 块时最多移动 $n$，因此换 l 块时总移动次数为 $O(\frac{n^2}{B})$，所以总移动次数为 $O(qB+\frac{n^2}{B})$。

所以总移动次数为 $O(\frac{c{n}^2}{B}+qB+\frac{n^2}{B})$。由于题目一般不会告诉你修改和询问分别的个数，所以统一用 $m$ 表示，可得总移动次数为 $O(\frac{m{n}^2}{B}+mB+\frac{n^2}{B})$。如果认为 $n,m$ 同阶，那么总移动次数为 $O(\frac{n^3}{B}+nB+\frac{n^2}{B})$，当 $B=n^{\frac{2}{3}}$ 时取最优复杂度 $O(n^{\frac{5}{3}})$。

P1903 [国家集训队] 数颜色 / 维护队列

板子题，不讲了，维护一下每个数的颜色和出现次数，按上面说的做就行。

回滚莫队（不删除莫队）

莫队的一个条件是需要在一个可以接受的复杂度内从 $[l,r]$ 转移到 $[l+1,r],[l-1,r],[l,r+1],[l,r-1]$，然而有的信息并不支持快速删除（比如取 $max$）。回滚莫队就是用来解决这类问题，我们只需要支持按顺序撤销，而不需要删除信息。

具体的方法如下：首先还是对询问排序，排序时以左端点所在块为第一关键字，右端点位置为第二关键字。我们把左端点在同一块内的询问一起处理，设这一块的左端点为 $L$，右端点为 $R$，初始时令 $l\to R+1$，$r\to R$，表示初始的空区间。对于每个询问，如果其左右端点都在该块内，那么我们直接暴力，复杂度为 $O(\sqrt{n})$。对于剩下的询问，每处理一个询问都先将 $r$ 移动到询问的右端点，保存此时的信息，然后将 $l$ 移动到左端点求出答案，最后令 $l\to R+1$，利用保存下的信息回滚到原来的状态。

分析一下该做法的复杂度：每块内，右端点单调递增，移动的次数为 $O(n)$，一共有 $O(\sqrt{n})$ 块，因此右端点移动的总次数为 $O(n\sqrt{n})$。对于左端点，每个询问移动次数为 $O(\sqrt{n})$，共有 $n$ 个询问，因此左端点移动的总次数为 $O(n\sqrt{n})$。暴力部分的总复杂度为 $O(n\sqrt{n})$，因此总复杂度就是 $O(n\sqrt{n})$。

AT1219 歴史の研究

板子题，不讲了，维护一下每个数的出现次数，按上面说的做就行。

P5906 【模板】回滚莫队&不删除莫队

和上一题差不多，维护一下每个数最左和最右的位置，然后跑回滚莫队即可。

树上莫队

其实，莫队算法除了序列还可以用于树。复杂度和序列上的莫队相同。

树分块

我们需要先解决一个问题，类似普通莫队，我们如何对一颗树进行分块？更形式化地说，对于给定的常数 $B$，我们需要使得每块的大小在 $[B,3B]$ 内，并且块内每个点到核心点路径上的所有点都在块内（同一个点可以成为多个块的核心点）。

先给出如下构造方式，再予以证明：

我们对整棵树进行 DFS，并创建一个栈，DFS 一个点时先记录初始栈顶高度，每 DFS 完当前节点的一棵子树就判断栈内新增节点的数量是否 $\ge B$，是则将栈内所有新增点分为同一块，核心点为当前 DFS 的点。当前节点结束 DFS 时将当前节点入栈，DFS 结束后将栈内所有剩余节点归入已经分好的最后一个块。

每块大小 $\ge B$ 是显然的。下面证明每个块大小 $\le 3B$：

对于当前节点的每一棵子树：

• 若未被分块的节点数 $>B$，那么在 DFS 这棵子树的根节点时就一定会把这棵子树的一部分分为一块直至这棵子树的剩余节点数 $\le B$，所以这种情况不存在。

• 若未被分块的节点数 $=B$，这些节点一定会和栈中所有节点分为一块，栈中之前还剩 $[0,B-1]$ 个节点，那么这一块的大小为 $[B,2B-1]$。

• 若未被分块的节点数 $<B$，当未被分块的节点数+栈中剩余节点数 $\ge B$ 时，这一块的大小在 $[B,2B-1)$ 内，否则继续进行下一棵子树。

对于 DFS 结束后栈内剩余节点，其数量一定在 $[1,B]$ 内，而已经分好块的每一块的大小在 $[B,2B-1]$ 之内，所以每块的大小都在 $[B,3B)$ 内。

修改方式

类似序列上的莫队，我们需要从某个询问 $(cu,cv)$ 转移至询问 $(tu,tv)$。

下文中 $T(u,v)$ 表示 $u\to v$ 的路径上除了 $lca(u,v)$ 以外的所有点构成的集合，$S(u,v)$ 表示 $u\to v$ 的路径，$\oplus$ 表示集合对称差。$cu,cv$ 为当前指针，$vis$ 数组记录每个节点是否在 $T(cu,cv)$ 内。按照如下方式更新：

• 由 $T(cu,cv)$ 更新至 $T(tu,tv)$ 时，将 $T(cu,tu)$ 和 $T(cv,tv)$ 的 $vis$ 分别取反，并相应地更新答案。

• 记录答案时对 $lca(cu,cv)$（此时 $cu,cv$ 已经变为了上面的 $tu,tv$）的 $vis$ 取反并更新答案，记录后再恢复。

对第二步的证明：

$$\begin{array}{rl}T(cu,cv)\oplus T(tu,tv)& =(S(cu,root)\oplus S(cv,root))\oplus (S(tu,root)\oplus S(tv,root))\\ & =(S(cu,root)\oplus S(tu,root))\oplus (S(cv,root)\oplus S(tv,root))\\ & =T(cu,tu)\oplus T(cv,tv)\end{array}$$

把 $T(cu,cv)\oplus T(tu,tv)$ 转化为 $T(cu,tu)\oplus T(cv,tv)$ 之后就可以通过对询问排序来降低复杂度。排序方式就是以 $u$ 所在块编号为第一关键字，$v$ 的编号为第二关键字排序，如果是带修莫队还要加上时间为第三关键字。树上莫队的单点修改和序列莫队类似，唯一不同的是用一个数组判断是否更新答案。复杂度分析和序列上的莫队类似，这里不做展开了。

括号序

另一种做法是将树的括号序分块，然后在上面跑莫队。事实上，无论常数还是代码复杂度，括号序都比树分块要更优。

具体实现就开一个 $vis$ 数组表示现在这个点的贡献是否计算，每次经过将 $vis$ 取反。但还有一些细节：如果 $lca$ 不是路径端点，那么它的贡献不会被计算，这需要特判。相对的，如果起点不是 $lca$，那么它的贡献不会被计算，这也需要特判。

P4074 [WC2013] 糖果公园

板子题，在括号序上跑带修莫队就行了。