深度学习（六）激活函数

激活函数是用来加入非线性因素的，解决线性模型所不能解决的问题。

 

激活函数通常有如下一些性质：

1. 非线性： 当激活函数是线性的时候，一个两层的神经网络就可以逼近基本上所有的函数了。但是，如果激活函数是恒等激活函数的时候（即f(x)=x），就不满足这个性质了，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的。
2. 可微性： 当优化方法是基于梯度的时候，这个性质是必须的。
3. 单调性： 当激活函数是单调的时候，单层网络能够保证是凸函数。
4. f(x)≈x： 当激活函数满足这个性质的时候，如果参数的初始化是random的很小的值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要很用心的去设置初始值。
5. 输出值的范围： 当激活函数输出值是 有限 的时候，基于梯度的优化方法会更加 稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是 无限 的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的learning rate.

 

首先我们有这个需求，就是二分类问题，如我要将下面的三角形和圆形点进行正确的分类，如下图：

 

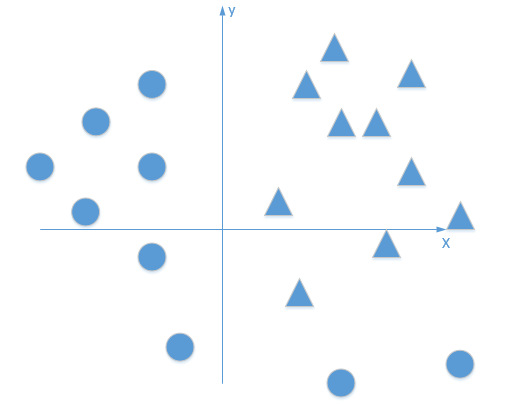
利用我们单层的感知机, 用它可以划出一条线, 把平面分割开：

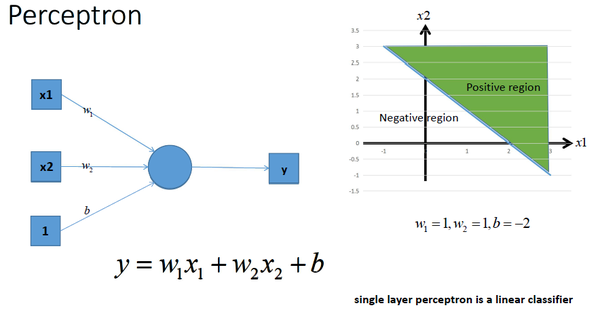
上图直线是由得到，那么该感知器实现预测的功能步骤如下，就是我已经训练好了一个感知器模型，后面对于要预测的样本点，带入模型中，如果,那么就说明是直线的右侧，也就是正类（我们这里是三角形），如果,那么就说明是直线的左侧，也就是负类（我们这里是圆形），虽然这和我们的题目关系不大，但是还是提一下~

好吧，很容易能够看出，我给出的样本点根本不是线性可分的，一个感知器无论得到的直线怎么动，都不可能完全正确的将三角形与圆形区分出来，那么我们很容易想到用多个感知器来进行组合，以便获得更大的分类问题，好的，下面我们上图，看是否可行：

 

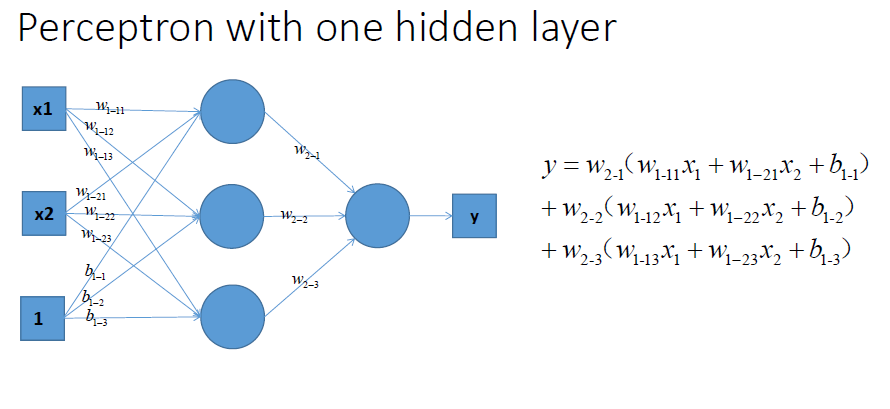
好的，我们已经得到了多感知器分类器了，那么它的分类能力是否强大到能将非线性数据点正确分类开呢~我们来分析一下：

我们能够得到

哎呀呀，不得了，这个式子看起来非常复杂，估计应该可以处理我上面的情况了吧，哈哈哈哈~不一定额，我们来给它变个形.上面公式合并同类项后等价于下面公式：

啧啧，估计大家都看出了，不管它怎么组合，最多就是线性方程的组合，最后得到的分类器本质还是一个线性方程，该处理不了的非线性问题，它还是处理不了。

就好像下图，直线无论在平面上如果旋转，都不可能完全正确的分开三角形和圆形点：

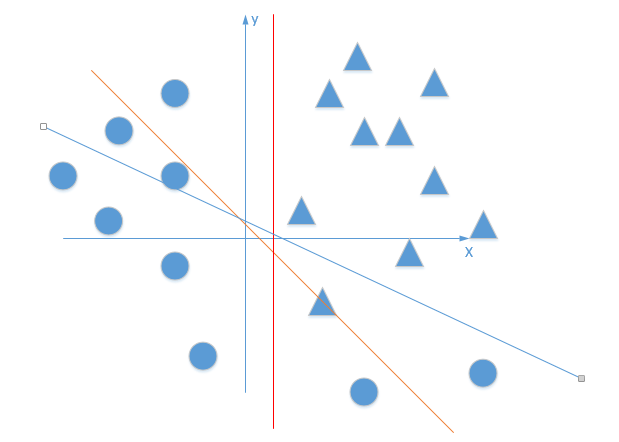
既然是非线性问题，总有线性方程不能正确分类的地方~

那么抛开神经网络中神经元需不需要激活函数这点不说，如果没有激活函数，仅仅是线性函数的组合解决的问题太有限了，碰到非线性问题就束手无策了.那么加入激活函数是否可能能够解决呢？

在上面线性方程的组合过程中，我们其实类似在做三条直线的组合，如下图：

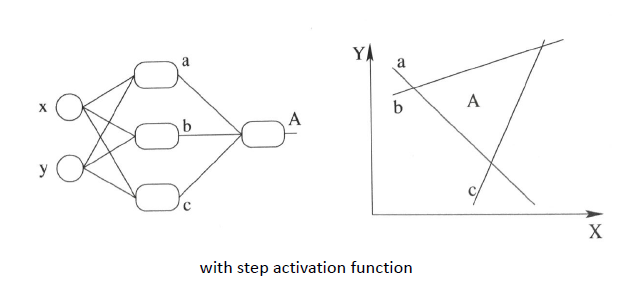
下面我们来讲一下激活函数，我们都知道，每一层叠加完了之后，我们需要加入一个激活函数（激活函数的种类也很多，如sigmoid等等~）这里就给出sigmoid例子，如下图：

 

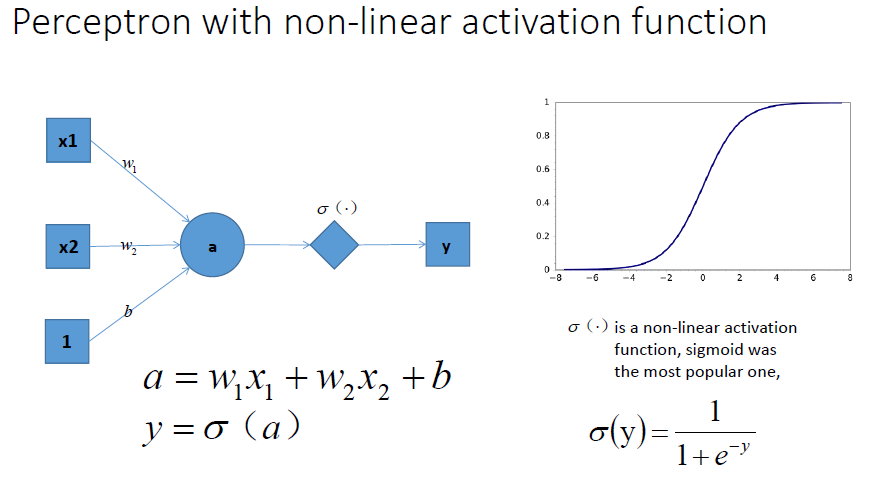
通过这个激活函数映射之后，输出很明显就是一个非线性函数！能不能解决一开始的非线性分类问题不清楚，但是至少说明有可能啊，上面不加入激活函数神经网络压根就不可能解决这个问题~

同理，扩展到多个神经元组合的情况时候，表达能力就会更强~对应的组合图如下：（现在已经升级为三个非线性感知器在组合了）

 

 

跟上面线性组合相对应的非线性组合如下：

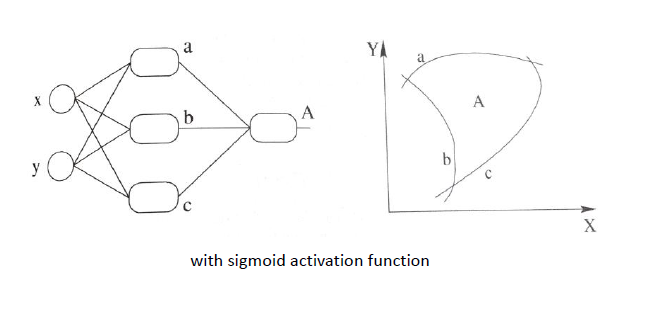
这看起来厉害多了，是不是~最后再通过最优化损失函数的做法，我们能够学习到不断学习靠近能够正确分类三角形和圆形点的曲线，到底会学到什么曲线，不知道到底具体的样子，也许是下面这个~

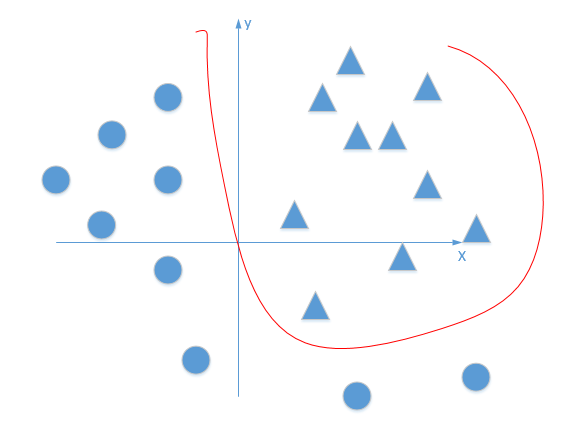
那么随着不断训练优化，我们也就能够解决非线性的问题了~

所以到这里为止，我们就解释了这个观点，加入激活函数是用来加入非线性因素的，解决线性模型所不能解决的问题。

 

下面就以Sigmoid为例，介绍激活函数的使用：

Sigmoid函数

它能够把输入的连续实值“压缩”到0和1之间。 
特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1. 我的个人理解是：输出0-1之间的概率，或者使用其他的激活函数，可以使值都规则化在一个区间中，有助于分类（输出层）或计算（隐含层）