卷积神经网络--CNN

1.人工神经网络

    神经网络由大量的节点（或称“神经元”、“单元”）和相互连接而成。每个神经元接受输入的线性组合，进行非线性变换（亦称激活函数activation function）后输出。每两个节点之间的连接代表加权值，称之为权重（weight）。不同的权重和激活函数，则会导致神经网络不同的输出。

    举个手写识别的例子，给定一个未知数字，让神经网络识别是什么数字。此时的神经网络的输入由一组被输入图像的像素所激活的输入神经元所定义。在通过激活函数进行非线性变换后，神经元被激活然后被传递到其他神经元。重复这一过程，直到最后一个输出神经元被激活。从而识别当前数字是什么字。

     神经网络的每个神经元/单元如下

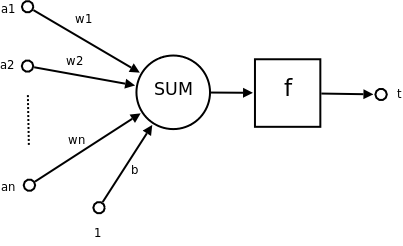
    类似wx + b的形式，其中

• a1~an为输入向量，当然，也常用x1~xn表示输入
• w1~wn为权重
• b为偏置bias
• f 为激活函数
• t 为输出

    如果只是上面这样一说，估计以前没接触过的十有八九又必定迷糊了。事实上，在20世纪50/60年代，上述简单神经元被称之为感知机，可以把感知机理解为一个根据不同因素、以及各个因素的重要性程度而做决策的模型。

    举个例子，这周末北京有一草莓音乐节，那去不去呢？决定你是否去有3个因素，这三个因素可以对应三个输入，分别用x1、x2、x3表示，此外，这三个因素对做决策的影响程度不一样，各自的影响程度用权重w1、w2、w3表示。一般来说，音乐节的演唱嘉宾会非常影响你去不去，唱得好的前提下 即便天气不好、没人陪同都可忍受，但如果唱得不好还不如你上台唱呢。所以，我们可以如下表示：

• x1：是否有喜欢的演唱嘉宾。x1 = 1 你喜欢这些嘉宾，x1 = 0 你不喜欢这些嘉宾。嘉宾因素的权重w1 = 5
• x2：天气好坏。x2 = 1 天气好，x2 = 0 天气不好。天气权重w2 = 2。
• x3：是否有人陪你同去。x3 = 1 有人陪你同去，x2 = 0 没人陪你同去。是否有陪同的权重w3 = 3。

    这样，咱们的决策模型函数便建立起来了：f(x) = g( w1*x1 + w2*x2 + w3*x3 + b )，g表示激活函数。不同的输入会得到不一样的决策结果。

 

1.2 激活函数

    常用的激活函数有sigmoid、tanh、relu等等，前两者sigmoid/tanh比较常见于全链接层，后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数。

　sigmoid的函数表达式如下:

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

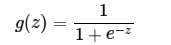
    其中z是一个线性组合，比如z可以等于：w0 + w1*x1 + w2*x2。通过代入很大的正数或很小的负数到函数中可知，g(z)结果趋近于0或1。

    因此，sigmoid函数的图形表示如下：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

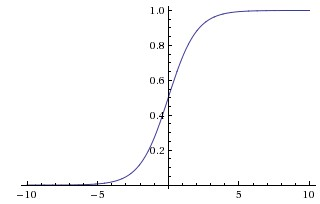
    也就是说，sigmoid函数的功能是相当于把一个实数压缩至0到1之间。输入非常大的正数时，输出结果会接近1，而输入非常大的负数时，则会得到接近0的结果。压缩至0到1有何用处呢？用处是这样一来变可以把激活函数看作一种“分类的概率”，比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。

 

1.3 神经网络

    将下图的这种单个神经元

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

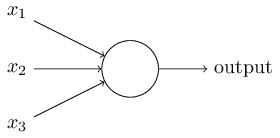
    组织在一起，便形成了神经网络。下图便是一个三层神经网络结构

　　　　　　　　　　　　　　　　　　　　　　　　　　

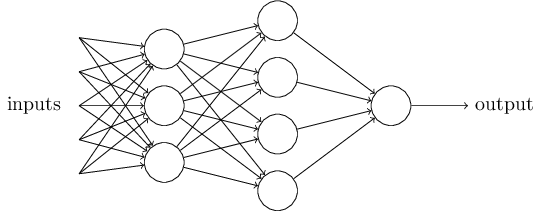
    上图中最左边的原始输入信息称之为输入层，最右边的神经元称之为输出层（上图中输出层只有一个神经元），中间的叫隐藏层。

    啥叫输入层、输出层、隐藏层呢？

• 输入层（Input layer），众多神经元（Neuron）接受大量非线形输入讯息。输入的讯息称为输入向量。
• 输出层（Output layer），讯息在神经元链接中传输、分析、权衡，形成输出结果。输出的讯息称为输出向量。
• 隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。如果有多个隐藏层，则意味着多个激活函数。

    同时，每一层都可能由单个或多个神经元组成，每一层的输出将会作为下一层的输入数据。比如下图中间隐藏层来说，隐藏层的3个神经元a1、a2、a3皆各自接受来自多个不同权重的输入，接着，a1、a2、a3又在自身各自不同权重的影响下 成为的输出层的输入，最终由输出层输出最终结果。

 

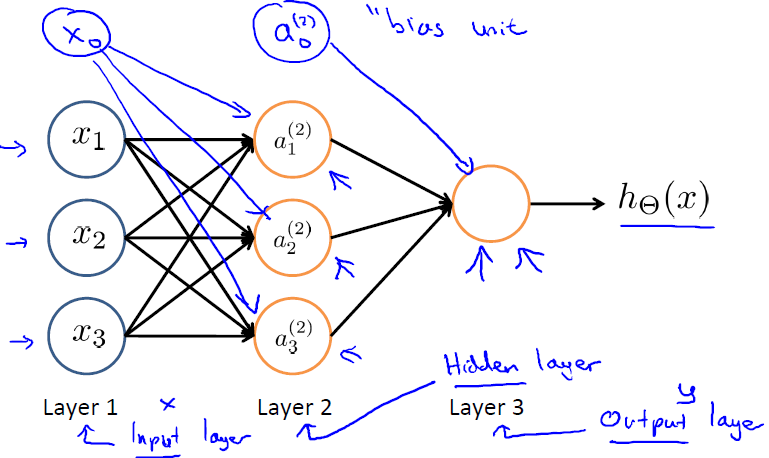
• 表示第j层第i个单元的激活函数
• 表示从第j层映射到第j+1层的控制函数的权重矩阵 (俗话讲就是权重跟输入经过一定数学公式形成一定的值)

    此外，输入层和隐藏层都存在一个偏置（bias unit)，所以上图中也增加了偏置项：x0、a0。针对上图，有如下公式

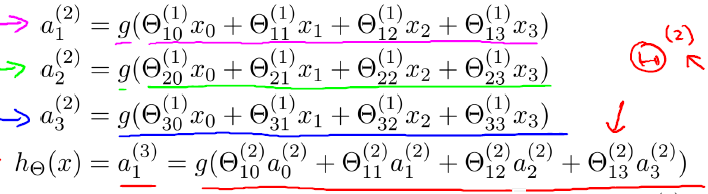
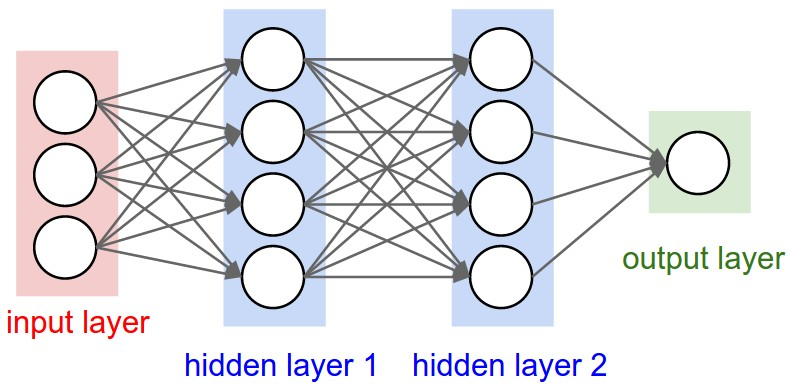
    此外，上文中讲的都是一层隐藏层，但实际中也有多层隐藏层的，即输入层和输出层中间夹着数层隐藏层，层和层之间是全连接的结构，同一层的神经元之间没有连接。

 

2. 卷积神经网络之层级结构

　　卷积神经网络各个层级结构，如下图:

 

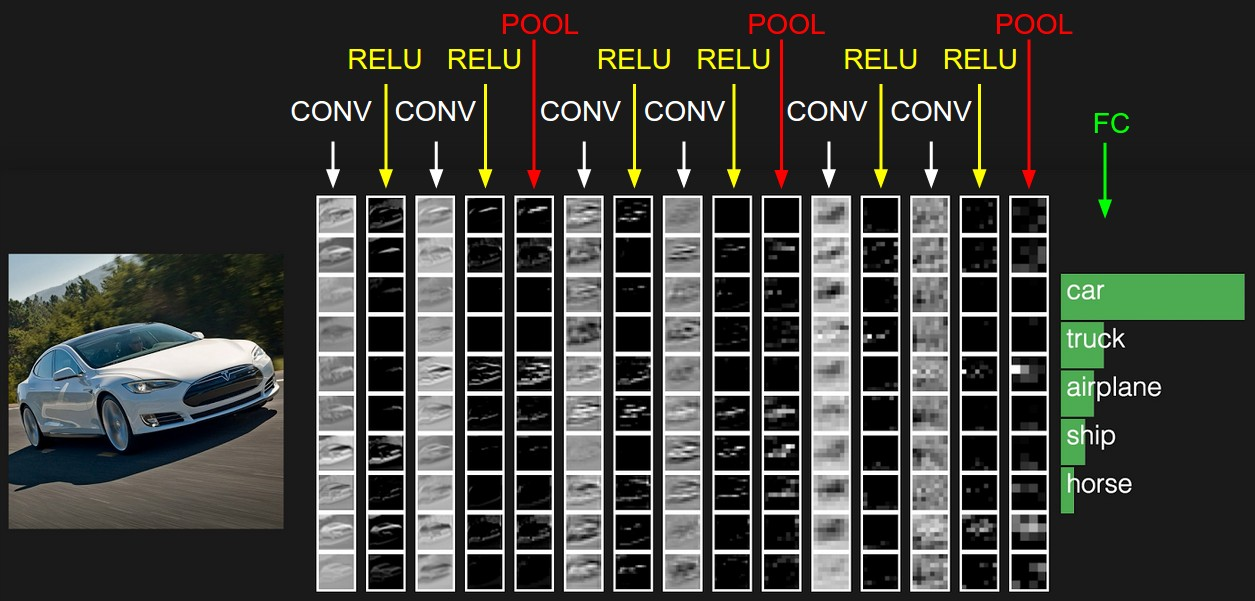
    上图中CNN要做的事情是：给定一张图片，是车还是马未知，是什么车也未知，现在需要模型判断这张图片里具体是一个什么东西，总之输出一个结果：如果是车 那是什么车

 所以

• 最左边是数据输入层，对数据做一些处理，比如去均值（把输入数据各个维度都中心化为0，避免数据过多偏差，影响训练效果）、归一化（把所有的数据都归一到同样的范围）、PCA/白化等等。CNN只对训练集做“去均值”这一步。

 

中间是

• CONV：卷积计算层，线性乘积求和(利用不同的卷积核求出不同的矩阵)。
• RELU：激励层，ReLU是激活函数的一种。
• POOL：池化层，简言之，即取区域平均或最大。

 

    最右边是

• FC：全连接层

    这几个部分中，卷积计算层是CNN的核心。

 

3.CNN之卷积计算层

3.1 什么是卷积

    首先，我们来了解下什么是卷积操作。

    对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的权重固定，所以又可以看做一个恒定的滤波器filter，也可以叫做卷积核）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源，通俗点就是取出这张图片的特征。

    比如下图中，图中左边部分是原始输入数据，图中中间部分是滤波器filter，图中右边是输出的新的二维数据。

 

　　　　　　　　　　　　　　　　　　

 

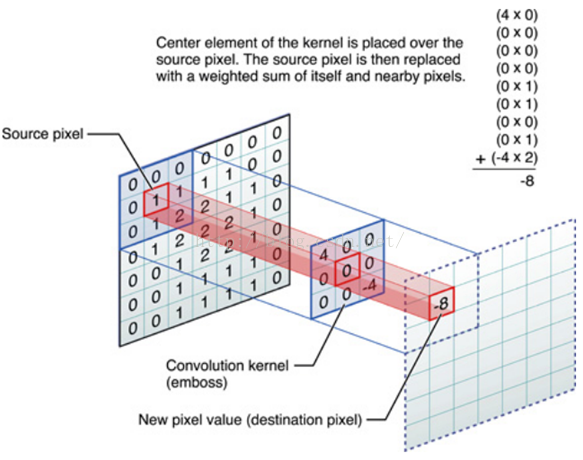
    分解下上图

　　　　　　　　

　　　　　　

 

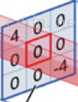
　　　　　　对应位置上是数字先乘后相加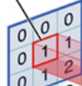

　　　　　　=

 

     中间滤波器filter与数据窗口做内积，其具体计算过程则是：4*0 + 0*0 + 0*0 + 0*0 + 0*1 + 0*1 + 0*0 + 0*1 + -4*2 = -8

 

3.2 多卷积核

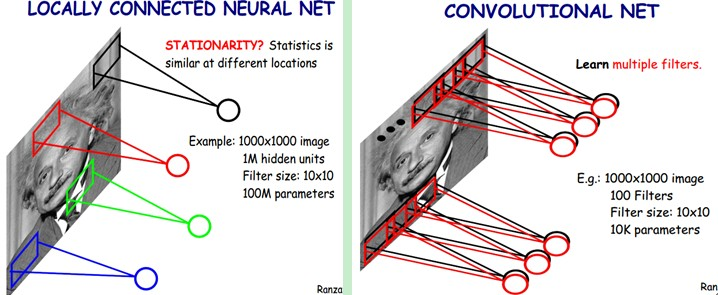
如果只有100个参数时，表明只有1个10*10的卷积核，显然，特征提取是不充分的，我们可以添加多个卷积核，比如32个卷积核，可以学习32种特征。在有多个卷积核时，如下图所示：

 

 

3.3 图像上的卷积

    在计算过程中，输入是一定区域大小(width*height)的数据和滤波器filter（一组固定的权重）做内积后等到新的二维数据。

    对于下图中，左边是图像输入，中间部分就是滤波器filter（一组固定的权重），不同的滤波器filter会得到不同的输出数据，比如轮廓、颜色深浅。相当于如果想提取图像的不同特征，则用不同的滤波器filter，提取想要的关于图像的特定信息：轮廓或颜色深浅。

    如下图所示:

　　　　　　　　　　　　

 

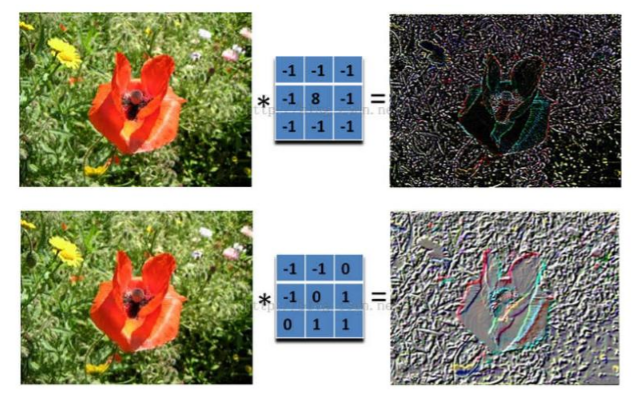
3.4 cs231d的动态卷积图 

    cs231n课程中，给了一张动图，网址是：http://cs231n.github.io/assets/conv-demo/index.html

    如果初看此图，可能不一定能立马理解啥意思，但结合上文的内容后，理解这个动图已经不是很困难的事情。

    下述动图中，左边是输入，中间部分是两个不同的滤波器Filter w0、Filter w1，最右边则是两个不同的输出。

 

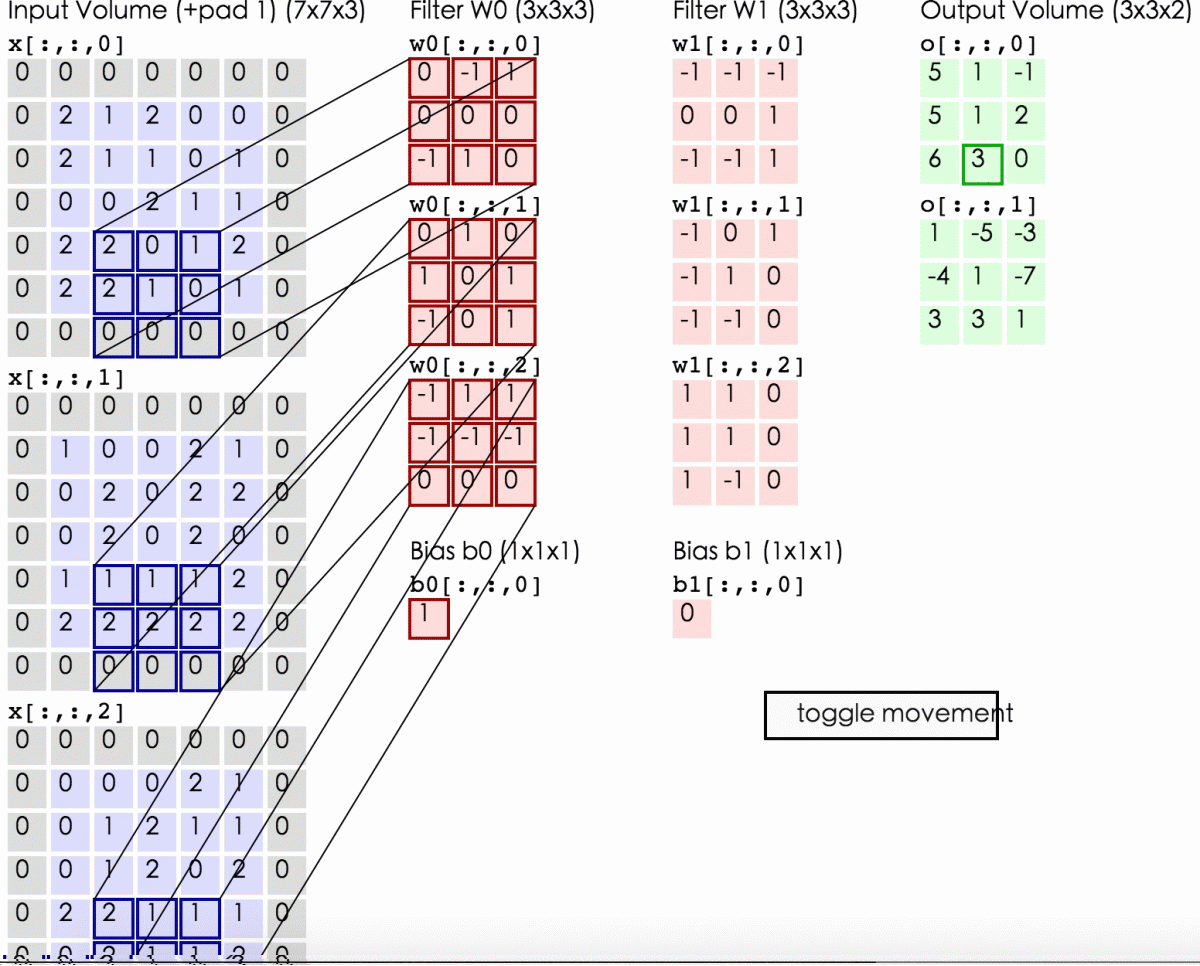
    随着左边数据窗口的平移滑动，滤波器Filter w0对不同的局部数据进行卷积计算。

    值得一提的是：

• 左边数据在变化，每次滤波器都是针对某一局部的数据窗口进行卷积，这就是所谓的CNN中的局部感知机制。
• 与此同时，数据窗口滑动，但中间滤波器Filter w0的权重（即每个神经元连接数据窗口的的权重）是固定不变的，这个权重不变即所谓的CNN中的参数共享机制。

    我第一次看到上面这个动态图的时候，只觉得很炫，另外就是据说“相乘后想加”，但到底具体是个怎么相乘后想加的过程 则无法一眼看出，网上也没有一目了然的计算过程。本文来细究下。

    首先，我们来分解下上述动图，如下图

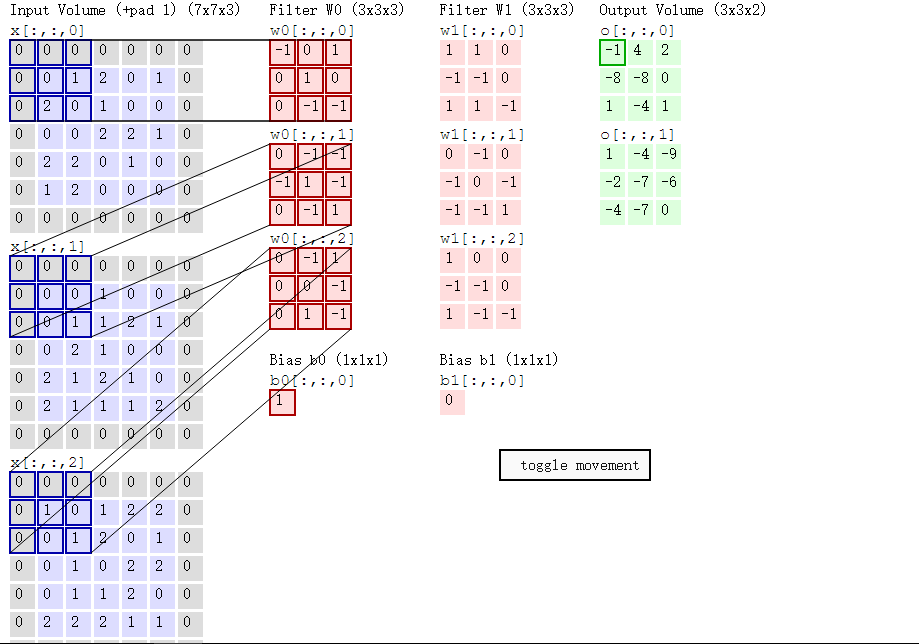
    接着，我们细究下上图的具体计算过程。即上图中的输出结果-1具体是怎么计算得到的呢？其实，类似wx + b，w对应滤波器Filter w0，x对应不同的数据窗口，b对应Bias b0，相当于滤波器Filter w0与一个个数据窗口相乘再求和后，最后加上Bias b0得到输出结果-1，如下过程所示：

　　　　　　　　　　　　　　　　　　　　　　　　

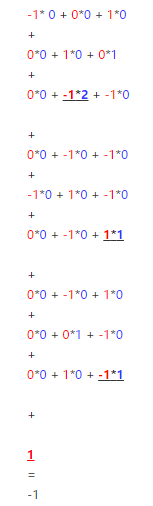
    然后滤波器Filter w0固定不变，数据窗口向右移动2步，继续做内积计算，得到4的输出结果

    最后，换做另外一个不同的滤波器Filter w1、不同的偏置Bias b1，再跟图中最左边的数据窗口做卷积，可得到另外一个不同的输出。

 

4.CNN之激励层与池化层

4.1 ReLU激励层

    1.2节介绍了激活函数sigmoid，但实际梯度下降中，容易饱和和终止梯度传递，且没有0中心化。咋办呢，可以尝试另外一个激活函数：ReLU，其图形表示如下：

　　　　　　　　　　　　　　　　　　　　　　　　

    ReLU的优点是收敛快，求梯度简单。

4.2 池化pool层（取出局部最明显的特征）

    前头说了，池化，简言之，即取区域平均或最大，如下图所示：

　　　　　　　　　　　　　　　　　　　　　　　　　　

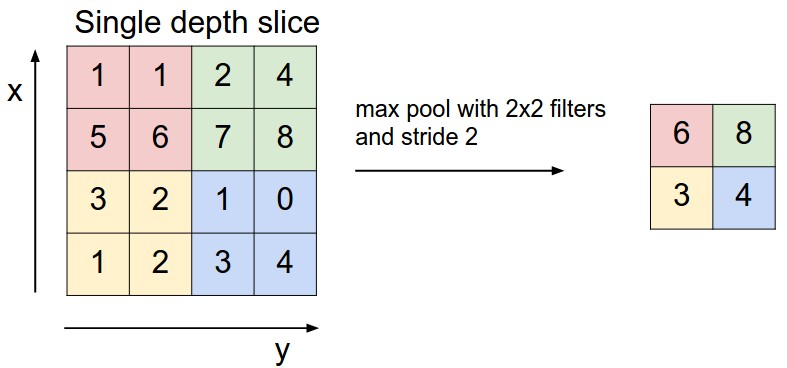
    上图所展示的是取区域最大，即上图左边部分中 左上角2x2的矩阵中6最大，右上角2x2的矩阵中8最大，左下角2x2的矩阵中3最大，右下角2x2的矩阵中4最大，所以得到上图右边部分的结果：6 8 3 4。

 

 总结：在经过多层卷积和池化以后会输出多张图片（也就是输入图片经过不同“处理”后的照片），可以把其称作Shape（很多原图片的特征图片组成），但是在计算机中是一个很大的数组。