CRF 详细推导、验证实例

逐帧softmax

CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧都进行分类，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示

条件随机场

然而，当我们设计标签时，比如用s、b、m、e的4个标签来做字标注法的分词，目标输出序列本身会带有一些上下文关联，比如s后面就不能接m和e，等等。逐标签softmax并没有考虑这种输出层面的上下文关联，所以它意味着把这些关联放到了编码层面，希望模型能自己学到这些内容，但有时候会“强模型所难”。CRF和编码层是两个不同的层。

BiLSTM-CRF model

我们只考虑4个标签

B-Person
I- Person
B-Organization
I-Organization
O

正如下图所示

1. 在每个句子中的词x被以词向量和字向量所表示

2. 模型输出的是这次词的命名实体识别的标签

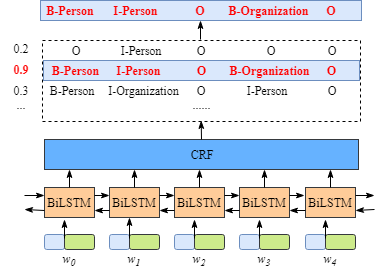
虽然，这没必要去了解BiLSTM的细节，但是为了了解CRF层更加清晰，你必须知道BiLSTM层输出内容的含义。

上面这张图已经阐述了BiLSTM输出对于每个label的打分

CRF Layer

CRF层学习的是标签之间的关联信息，也可以叫做约束信息，因为B-Peson后面不可能接I-Organization

在CRF层的损失函数有两个不同的分数，这两个分数是CRF层关键性的思想

1. Emission score（当前标签分数）

这个分数是来自编码器的输出，如下图所示：

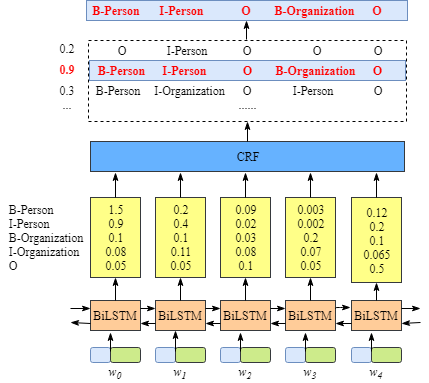
为了方便起见，我们给每个标签一个下标

Label	index
B-Person	0
I-Person	1
B-Organization	2
I-Organization	3
O	4

当我们用x_ij表示emission score, i是字在句子中的下标，y_i表示标签的下标，例如，x_i=1,yj=2=X_{w1,B-Oranization}=0.1，这表示字w₁会被标注为B-Organization的分数为0.1

2. Transition score（转移矩阵分数）

我们用t_yiyj表示转移分数，例如t_{B-Person,I-Person}=0.9代表B-Person->I-Person的分数为0.1，因此，我们有一个代表所有标签转移的转移矩阵。

为了让我们这个转移举证更加的强健，我们需要加入START和END，START代表的是一个句子的开始，不是代表第一个字；END代表的是一个句子的结尾，不是代表最后一个字。

转移矩阵的例子：下表是添加了START和END标签后的转移矩阵

	START	B-Person	I-Person	B-Organization	I-Organization	O	END
START	0	0.8	0.007	0.7	0.0008	0.9	0.008
B-Person	0	0.6	0.9	0.2	0.0006	0.6	0.009
I-Person	-1	0.5	0.53	0.55	0.0003	0.85	0.008
B-Organization	0.9	0.5	0.0003	0.25	0.8	0.77	0.006
I-Organization	-0.9	0.45	0.007	0.7	0.65	0.76	0.2
O	0	0.65	0.0007	0.7	0.0008	0.9	0.008
END	0	0	0	0	0	0	0

正如上表所看到的，我们可以看到转移矩阵可以学习某些约束性的特征：例如：B-Person->I-Organization的分数很小，I-Person->I-Organization的分数很小。

你可能会问，这个转移矩阵是从哪里学习到这些约束性的特征的？

事实上，这个矩阵是Encoder-CRF的参数，这个是随机初始化后，通过训练学习到的。换句话说，CRF层可以通过训练自己学习到。

3. 所有路径的总得分和真正路径得分

CRF与Softmax不同的是，Softmax把序列标注看成是n个k分类问题，后者将序列标注看成是一个1个kⁿ问题，从kⁿ路径中找出一条分值最大的路径，并且CRF是一个条件概率。

CRF在定义的时候，提出了两个假设

假设一 该分布是指数族分布。

这个假设意味着存在函数\[f({y_1},...,{y_n};x){\kern 1pt} \]使得

\[P({y_1},...,{y_n}|x) = \frac{1}{{Z(x)}}\exp (f({y_1},...,{y_n};x))\]

注：在这里x表示CRF层的输入，表示编码器的输出，y表示命名实体的标签。

其中Z(x)是归一化因子，因为这个是条件分布，所以归一化因子与x（输入）有关。这个f函数可以视为一个打分函数，打分函数取指数并归一化就得到了概率分布。

假设二 输出之间的关联仅发生在相邻位置，并且关联是指数加性的。

这个假设意味着存在函数\[f({y_1},...,{y_n};x)\]可以更进一步简化为

\[f({y_1},...,{y_n};x) = h({y_1};x) + g({y_1},{y_2};x) + h({y_2};x) + g({y_2},{y_3};x) + ... + g({y_{n - 1}},{y_n};x) + h({y_n};x)\]

所有路径的总得分

假设在某一时刻所有可能的路径都都一个分为P_i，并且总共有N条可能的路径，那么所有路径的总分为

\[P_t^{total} = P_t^1 + P_t^2 + ... + P_t^N = e_t^{{S_1}} + e_t^{{S_2}} + ... + e_t^{{S_N}}\]

注：e是自然对数

明确的点，这是下面递归求法的关键关键：

每个分量的分值标志上一个时刻，转移到这个分量标签的总分，总分表示这个时刻所有分量的的总分，相当于总分求了2次指数的和，而分量只求了一次。
t+1时刻的每个分量（每个标签）的结果 = t时刻所有分量的结果（这个shape为[B, N]） + 加上状态转移分值 (转移到t+1时刻分量的转移值) + t+1时刻的该标签的分值（编码器输出的值），然后再e指数再求和（这里为什么要e指数再求和，跟CRF的主题思想是一样的，哪条路径占是最大的概率），得到的结果才是该标签（指的是N个标签中的一个，分量的意思）在t+1时刻的结果，所有e指数求和才是t+1时刻的P_total

例如，如果我们数据集中有如下标签：

Label	Index
B-Person	0
I-Person	1
B-Organization	2
I-Organization	3
O	4
START	5
END	6

我们现在拿一个句子来举例，这个句子里面有5个字，它可能的标签是：

1) START B-Person B-Person B-Person B-Person B-Person END
2) START B-Person I-Person B-Person B-Person B-Person END
…
10) START B-Person I-Person O B-Organization O END
…
N) O O O O O O O

在上面的例子中，如果第10个是真正的路径，换句话说，这个是训练集中对应的路径，那么第10个路径的得分肯定是在P_total中最大的。

下面是CRF真正路径的概率公式，随着训练步数的增加，那么真正路径的概率肯定是一直增加的。

\[\Pr {\rm{o}}{{\rm{b}}_{{\mathop{\rm Re}\nolimits} alPath}} = \frac{{{P_{{\mathop{\rm Re}\nolimits} alPath}}}}{{{P_1} + {P_2} + ... + {P_N}}}\]

现在我们来用一个例子来进行讲解：

我们加入我们训练的句子只有3个字 x = {w₀, w₁, w₂}，而且在我们的数据集中标签就只有两个 label = {l₁, l₂}

1. Emission Score，这个分值是从编码器中输出来的:

	l₁	l₂
w₀	x₀₁	x₀₂
w₁	x₁₁	x₁₂
w₂	x₂₁	x₂₂

2. Transition Score，状态转移分数：

	l₁	l₂
l₁	t₁₁	t₁₂
l₂	t₂₁	t₂₂

3. 在计算的时候，我们要用到递归的思想，我们在这里定义两个名称：obs和previous，previous是求前面所有步骤的结果，obs是当前词在编码器中输出的信息

在w₀的时刻

obs = [x₀₁, x₀₂]

previous = None

相当于这一时刻的previous的result是编码器输出的值，所以 TotalScore(w₀) = log(e^x₀₁+e^x₀₂)，加上log是防止出现极小极大值

在w₁的时刻

obs = [x₁₁, x₁₂]

previous = [x₀₁, x₀₂]

复制previous维度，并扩展

\[previous = \left( \begin{array}{l}
{x_{01}},{x_{01}}\\
{x_{02}},{x_{02}}
\end{array} \right)\]

复制previous维度，并扩展

\[obs = \left( \begin{array}{l}
{x_{11}},{x_{12}}\\
{x_{11}},{x_{12}}
\end{array} \right)\]

注：扩展维度和复制维度的目的是为了让我们计算更加的方便

对previous, obs和transition的分数进行求和

\[\begin{array}{l}
scores = \left( \begin{array}{l}
{x_{01}},{x_{01}}\\
{x_{02}},{x_{02}}
\end{array} \right) + \left( \begin{array}{l}
{t_{11}},{x_{12}}\\
{x_{21}},{x_{22}}
\end{array} \right) + \left( \begin{array}{l}
{x_{11}},{x_{12}}\\
{x_{11}},{x_{12}}
\end{array} \right)\\
scores = \left( \begin{array}{l}
{x_{01}} + {t_{11}} + {x_{11}},{x_{01}} + {t_{12}} + {x_{12}}\\
{x_{02}} + {t_{21}} + {x_{11}},{x_{02}} + {t_{22}} + {x_{12}}
\end{array} \right)
\end{array}\]

红框中表示0时刻转移到1时刻的标签为1的每个路径的分值，取e指数然后求和就得到了1时刻标签为1的总分；1时刻标签为2同理。

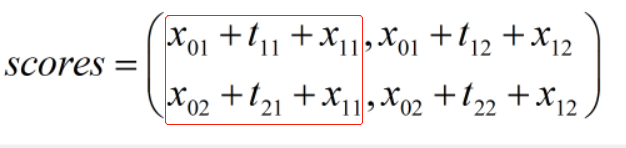
所以，previous的值为

\[previous = [\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}),\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}})]\]

注：这里求和是对某个标签求和，是在竖直方向求值，含义是：我这个标签这个时刻的总分

TotalScore为

\[\begin{array}{l}
TotalScore({w_0} \to {w_1}) = \log ({e^{previous[0]}} + {e^{previous[1]}})\\
TotalScore({w_0} \to {w_1}) = \log ({e^{\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}})}} + {e^{\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}})}})\\
TotalScore({w_0} \to {w_1}) = \log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}} + {e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}})
\end{array}\]

在w₂时刻

obs = [x₂₁, x₂₂]

previous = [log(e^{x₀₁+x₁₁+t₁₁}+e^{x₀₂+x₁₁+t₂₁}), log(e^{x₀₁+x₁₂+t₁₂}+e^{x₀₂+x₁₂+t₂₂})]

扩展和复制维度

\[previous = \left( \begin{array}{l}
\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}),\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}})]\\
\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}),\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}})]
\end{array} \right)\]

\[obs = \left( \begin{array}{l}
{x_{21}},{x_{22}}\\
{x_{21}},{x_{22}}
\end{array} \right)\]

socres

\[\begin{array}{l}
scores = \left( \begin{array}{l}
\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}),\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}})\\
\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}),\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}})
\end{array} \right) + \left( \begin{array}{l}
{t_{11}},{t_{12}}\\
{t_{21}},{t_{22}}
\end{array} \right) + \left( \begin{array}{l}
{x_{21}},{x_{22}}\\
{x_{21}},{x_{22}}
\end{array} \right)\\
scores = \left( \begin{array}{l}
\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}) + {t_{11}} + {x_{21}},\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}) + {t_{12}} + {x_{22}}\\
\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}) + {t_{21}} + {x_{21}},\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}) + {t_{12}} + {x_{22}}
\end{array} \right)
\end{array}\]

计算previous

\[\begin{array}{l}
previous = [\\
\log ({e^{\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}) + {t_{11}} + {x_{21}}}} + {e^{\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}) + {t_{21}} + {x_{21}}}}),\log ({e^{\log ({e^{{x_{01}} + {t_{11}} + {x_{11}}}} + {e^{{x_{02}} + {t_{21}} + {x_{11}}}}) + {t_{12}} + {x_{22}}}} + {e^{\log ({e^{{x_{01}} + {t_{12}} + {x_{12}}}} + {e^{{x_{02}} + {t_{22}} + {x_{12}}}}) + {t_{12}} + {x_{22}}}})\\
]
\end{array}\]

正确的路径得分（Real Path Score）

很明显，在所有的路径中只有一条是真正的路径，如上述例子 START B-Person I-Person O B-Organization O END 这种路径就只有一条，是唯一的，e^Si是在第某个时刻某个标签为i的得分，e^S₁+e^S₂+......+e^S_N为某个时刻所有标签的总得分

如何去计算S_i：S_i = EmissionScore + TransitionScore

Emission Score:

Emission Score = x_0,START + x_1,B-Person + x_2,I-Person + x_3,O + x_{4,B-Organization} + x_5,O + x_6,END

x_{index, label}是词x^th被选中时的分数
这些分数全部来自BiLSTM的输出
对于开始和结束标志的分数，我们设置为0

Transition Score:

Transition Score = t_{START->B-Person} + t_{B-Person->I-Person} + t_I-Person->O + t_{O->B-Organization} + t_{B-Organization->O} + t_O->END

t_{label1->label2}是转移矩阵中label1到label2的分数
这个分数来自CRF层，或许可以说这是CRF层的参数

4. 损失函数

正确路径的概率公式为：

\[\Pr {\rm{o}}{{\rm{b}}_{{\mathop{\rm Re}\nolimits} alPath}} = \frac{{{P_{{\mathop{\rm Re}\nolimits} alPath}}}}{{{P_1} + {P_2} + ... + {P_N}}}\]

我们一般遇到概率问题，一般是用MLE（极大似然）来计算loss，所以Loss Function为

\[\begin{array}{l}
LossFunction = - \log \frac{{{e^{{S_{{\mathop{\rm Re}\nolimits} alPath}}}}}}{{{e^{{S_1}}} + {e^{{S_2}}} + ... + {e^{{S_N}}}}}\\
LossFunction = - ({S_{{\mathop{\rm Re}\nolimits} alPath}} - \log ({e^{{S_1}}} + {e^{{S_2}}} + ... + {e^{{S_N}}}))\\
LossFunction = - (\sum\nolimits_{i = 1}^N {{x_{i,{y_i}}} + \sum\nolimits_{i = 1}^{N - 1} {{t_{{y_i},{y_{i + 1}}}}} } - \log ({e^{{S_1}}} + {e^{{S_2}}} + ... + {e^{{S_N}}}))
\end{array}\]

从上面推导可以看出

\[{e^{{S_1}}} + {e^{{S_2}}} + ... + {e^{{S_N}}}\]

就是我们计算的所有路径总得分；再减去一个真实路径下在预测时的分值

\[\sum\nolimits_{i = 1}^N {{x_{i,{y_i}}} + \sum\nolimits_{i = 1}^{N - 1} {{t_{{y_i},{y_{i + 1}}}}} } \]

注：x_{i, yi}表示在编码层输出的值， t_{yi, yi+1}表示转移矩阵的值；最后的值可以看成是总分 - 真实路径得分，这也符合我们的常识，如果所有路径的得分等于真实路径的分的话，那么loss就是0。

5.进行预测

首先我们还是定义Emission score矩阵和Transition score矩阵，这两个矩阵都是已经训练好了的，还是一个句子有3个字

Emission score

	l₁	l₂
w₀	x₀₁	x₀₂
w₁	x₁₁	x₁₂
w₂	x₂₁	x₂₂

Transition score

	l₁	l₂
l₁	t₁₁	t₁₂
l₂	t₂₁	t₂₂

采用Viterbi algorithm来进行预测

w₀时

因为w₀为第一个字，所有它的最后结果就是[x₀₁, x₀₂]，如果第一个时刻编码器对于标签的输出是[0.2, 0.8]，那么第一个时刻的标签就为2；因为在第一个时刻，它不从任何地方转移而来。所有没有转移矩阵的作用。

w0->w1时

obs = [x₁₁, x₁₂]

previous = [x₀₁, x₀₂]

previous扩展并复制维度

\[{\rm{pre}}vious = \left( \begin{array}{l}
previous[0],previous[0]\\
previous[1],previous[1]
\end{array} \right) = \left( \begin{array}{l}
{x_{01}},{x_{01}}\\
{x_{02}},{x_{02}}
\end{array} \right)\]

obs扩展并复制维度

\[obs = \left( \begin{array}{l}
obs[0],obs[0]\\
obs[1],obs[1]
\end{array} \right) = \left( \begin{array}{l}
{x_{11}},{x_{12}}\\
{x_{11}},{x_{12}}
\end{array} \right)\]

对previous，obs和转移矩阵求和

\[scores = \left( \begin{array}{l}
{x_{01}},{x_{01}}\\
{x_{02}},{x_{02}}
\end{array} \right) + \left( \begin{array}{l}
{t_{11}},{t_{12}}\\
{x_{21}},{t_{22}}
\end{array} \right) + \left( \begin{array}{l}
{x_{11}},{x_{12}}\\
{x_{11}},{x_{12}}
\end{array} \right) = \left( \begin{array}{l}
{x_{01}} + {t_{11}} + {x_{11}},{x_{01}} + {t_{12}} + {x_{12}}\\
{x_{02}} + {t_{21}} + {x_{11}},{x_{02}} + {t_{22}} + {x_{12}}
\end{array} \right)\]

下面的计算与上节所描述的有所不同

\[previous = [\max (scores[00],scores[10]),\max (scores[01],scores[11])]\]

如果我们的分数如下

\[scores = \left( \begin{array}{l}
{x_{01}} + {t_{11}} + {x_{11}},{x_{01}} + {t_{12}} + {x_{12}}\\
{x_{02}} + {t_{21}} + {x_{11}},{x_{02}} + {t_{22}} + {x_{12}}
\end{array} \right) = \left( \begin{array}{l}
0.2,0.3\\
0.5,0.4
\end{array} \right)\]

这个时刻的previous，这里不用求e指数求和，因为上面设计到了归一化因子，所以才要指数求和，而且上面也说了CRF在设计的时候就提出了假设

\[previous = [\max (scores[00],scores[10]),\max (scores[01],scores[11])] = [0.5,0.4]\]

注：这个表示了在这个时刻每个标签的最大的分值

那么这个时候的路径就为

\[path = [{l_2} \to {l_1}:0.5,{l_2} \to {l_2}:0.4]\]

在w₂的时候

obs = [x₂₁, x₂₂]

previous = [0.5, 0.4]

previous扩展并复制维度

\[{\rm{pre}}vious = \left( \begin{array}{l}
previous[0],previous[0]\\
previous[1],previous[1]
\end{array} \right) = \left( \begin{array}{l}
0.5,0.5\\
0.4,0.4
\end{array} \right)\]

obs扩展并复制维度

\[obs = \left( \begin{array}{l}
obs[0],obs[0]\\
obs[1],obs[1]
\end{array} \right) = \left( \begin{array}{l}
{x_{21}},{x_{22}}\\
{x_{21}},{x_{22}}
\end{array} \right)\]

求scores

\[scores = \left( \begin{array}{l}
0.5,0.5\\
0.4,0.4
\end{array} \right) + \left( \begin{array}{l}
{t_{11}},{t_{12}}\\
{t_{21}},{t_{22}}
\end{array} \right) + \left( \begin{array}{l}
{x_{21}},{x_{22}}\\
{x_{21}},{x_{22}}
\end{array} \right) = \left( \begin{array}{l}
0.5 + {t_{11}} + {x_{21}},0.5 + {t_{12}} + {x_{22}}\\
0.4 + {t_{21}} + {x_{21}},0.4 + {t_{22}} + {x_{22}}
\end{array} \right)\]

假如我们的得到的分数为

\[scores = \left( \begin{array}{l}
0.6,0.9\\
0.8,0.7
\end{array} \right)\]

得到previous

\[previous = [0.8,0.9]\]

得到path

\[path = [{l_2} \to {l_2} \to {l_1}:0.8,{l_2} \to {l_1} \to {l_2}:0.9]\]

所以最优路径为

\[{l_2} \to {l_1} \to {l_2}\]

posted @ 2019-08-01 18:06 下路派出所阅读(6063) 评论(0) 编辑收藏举报

刷新页面返回顶部

下路派出所