attention 汇总(持续)
Seq2seq Attention
Normal Attention

1. 在decoder端,encoder state要进行一个线性变换,得到r1,可以用全连接,可以用conv,取决于自己,这里不需要加激活函数。
2. decoder端t时刻的输入和上一时刻的context vector(相当于在这个时刻,用上一时刻的state求context vector,然后再输入LSTM求出cell output)做一个线性变换(先拼接再输入到一个全连接网络),得到LSTM的输入;LSTM输出output和state,output可以用来经过一个线性变换求词表,state用于计算attention,这一个的求attention相当于是为下一步求attention(前面所说到的context vector)
1)在训练时,第一的时间步骤时,context vector为0
2)在预测时,context vector为encoder输出的state经过attention后的结果
c. 用state经过一个线性变化,并加上bias,就等于这部分 WS * st + b,得到r2,shape [batch_size, embedd_size]
d. 最后再经过vt * tanh(r1 + r2)得到的r3,再对r3进行求和,得到r4, shape [batch_size, time_step], 最后再经过softmax,shape [batch_size, time_step],这里要经过mask,即让为0的部分概率为0
加性Attention
当seq2seq decoder段去解码时,是每个时间步骤去与encoder端的进行attention,所以加性attention为
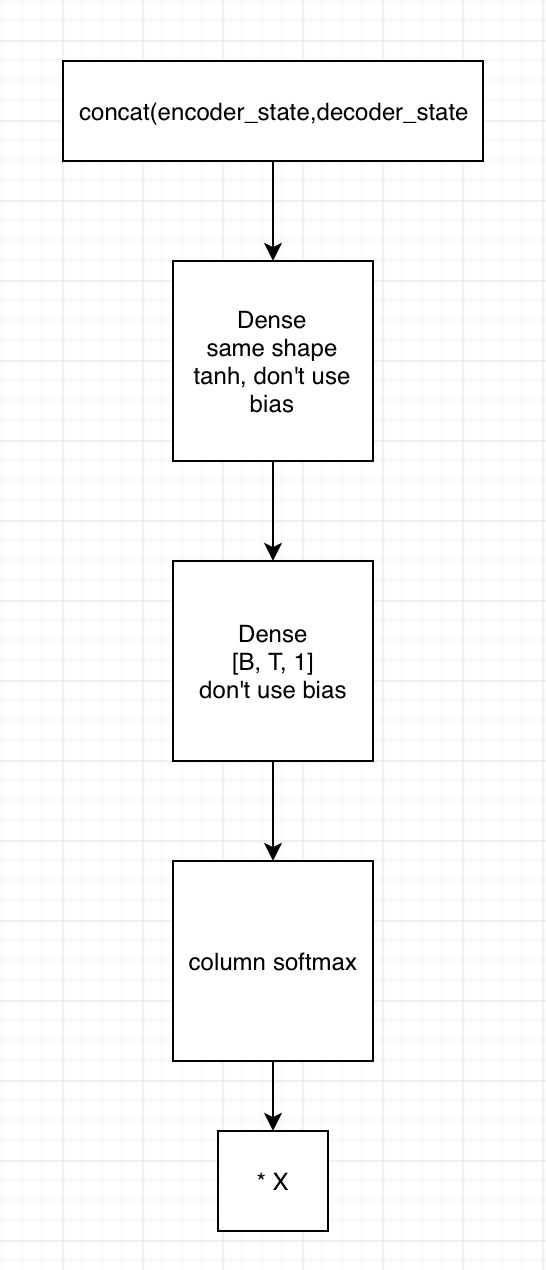
1. decoder端t时刻的输入和上一时刻的context vector(相当于在这个时刻,用上一时刻的state求context vector,然后再输入LSTM求出cell output)做一个线性变换(先拼接再输入到一个全连接网络),得到LSTM的输入;LSTM输出output和state,output可以用来经过一个线性变换求词表,state用于计算attention,这一个的求attention相当于是为下一步求attention(前面所说到的context vector)
1)在训练时,第一的时间步骤时,context vector为0
2)在预测时,context vector为encoder输出的state经过attention后的结果
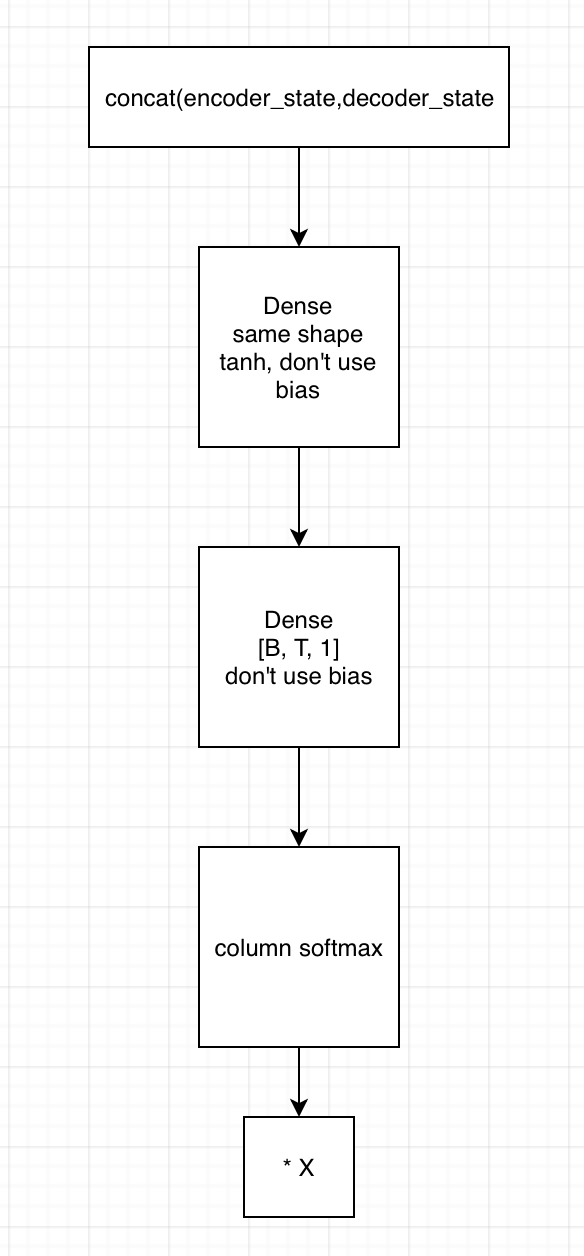
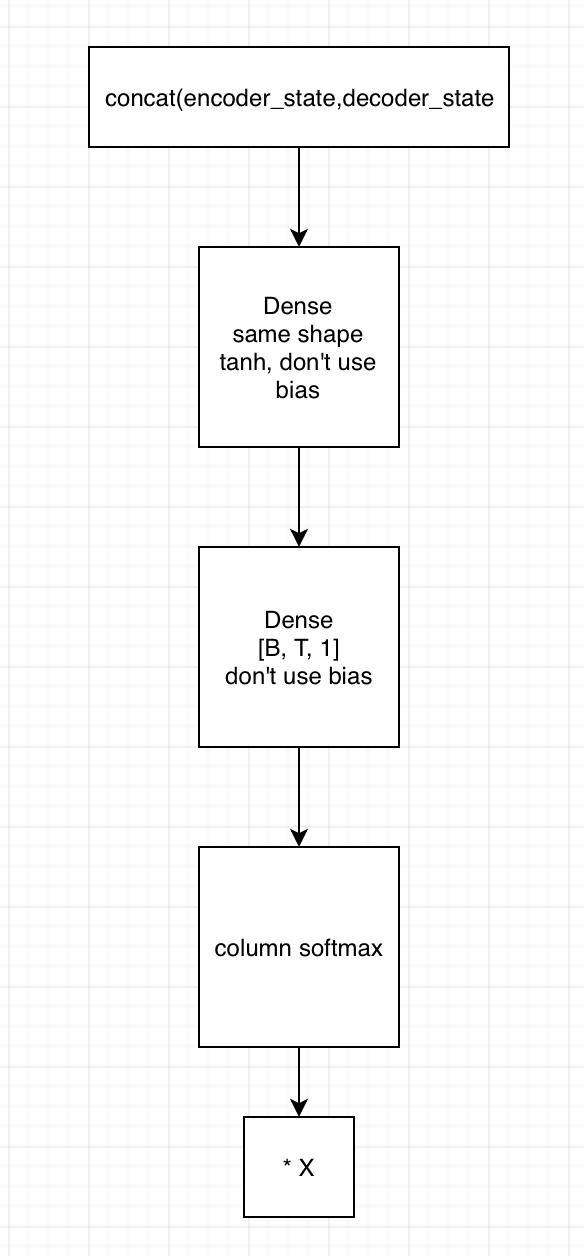
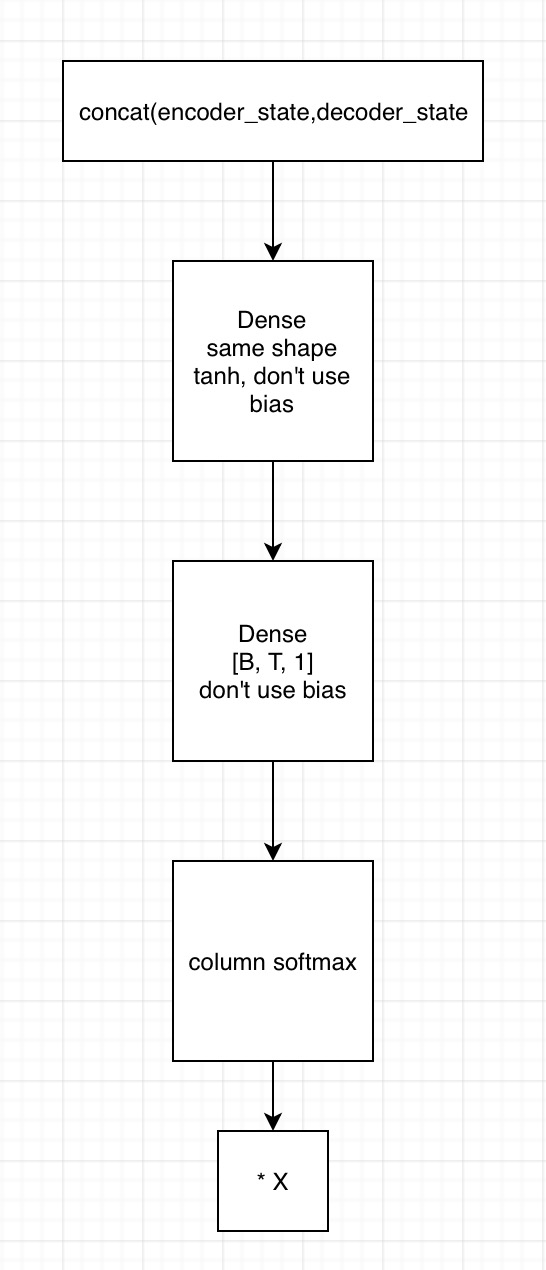
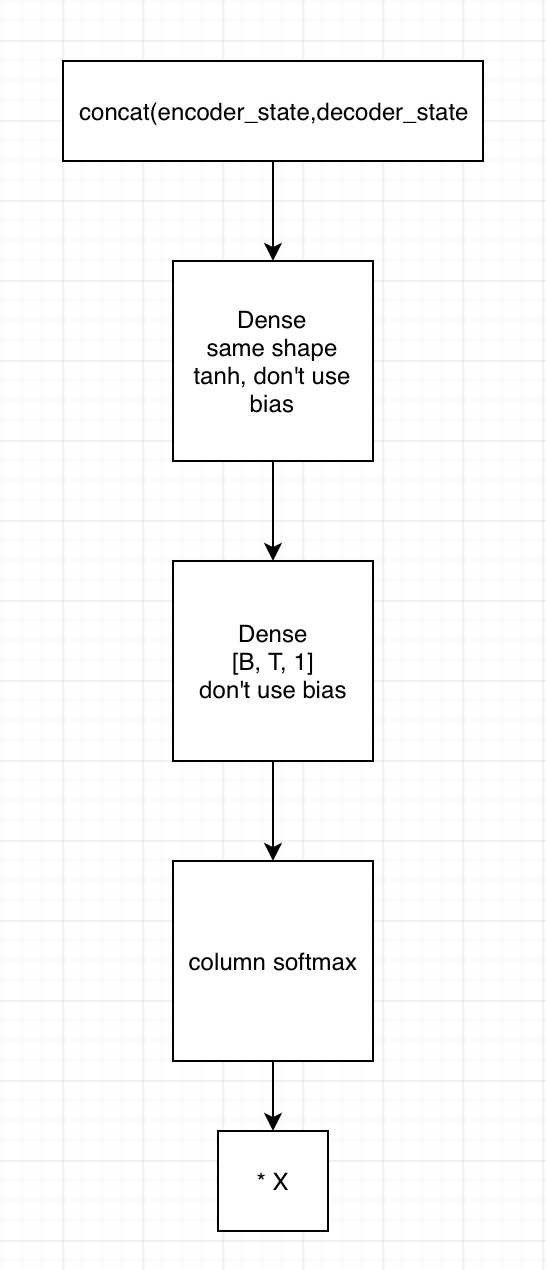
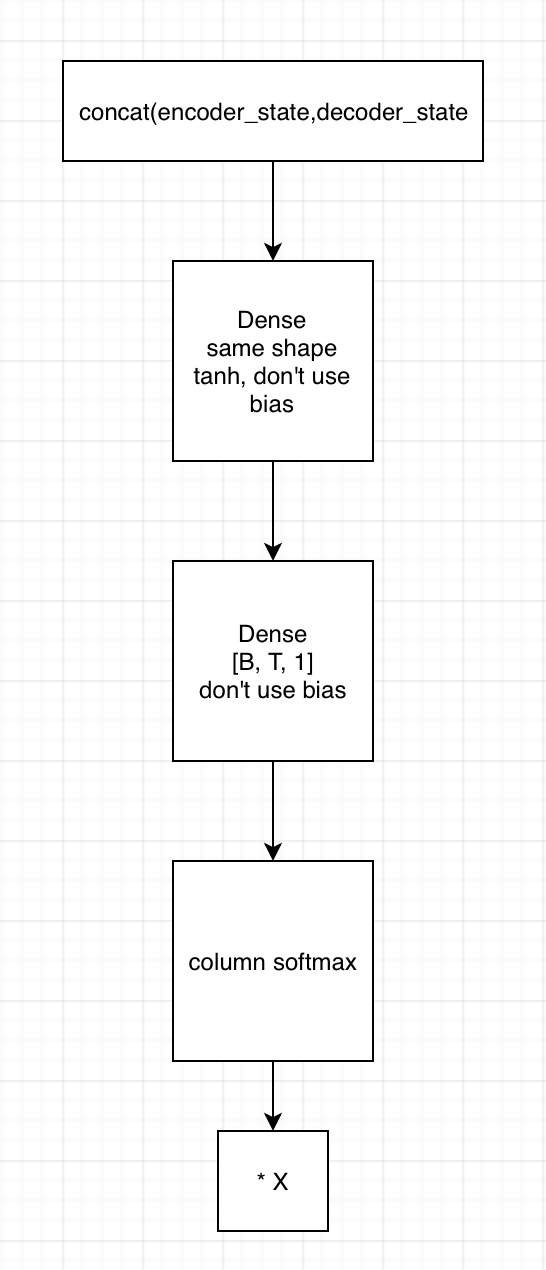
2. 用state拼接编码器的输出,得到[B, T, embedding1]
1)输入到第一个全连接神经网络,不采用bias,激活函数用tanh,shape保持一致
2) 将上一全连接神经网络的输出,输入到下一个全连接神经网络,不用激活函数,不加bias,shape为[B, T, 1]
3)在列的维度上求softmax,相当于求了每个时间的贡献度,这里要进行mask
4)相乘encoder端的输出,得到[B, T, embedding2],这里可以用来求context vector了(只需要在时间的维度上相加就行)
Self Attention
All Attention Is You Need
先来看一个翻译的例子“I arrived at the bank after crossing the river” 这里面的bank指的是银行还是河岸呢,这就需要我们联系上下文,当我们看到river之后就应该知道这里bank很大概率指的是河岸。在RNN中我们就需要一步步的顺序处理从bank到river的所有词语,而当它们相距较远时RNN的效果常常较差,且由于其顺序性处理效率也较低。Self-Attention则利用了Attention机制,计算每个单词与其他所有单词之间的关联,在这句话里,当翻译bank一词时,river一词就有较高的Attention score。利用这些Attention score就可以得到一个加权的表示,然后再放到一个前馈神经网络中得到新的表示,这一表示很好的考虑到上下文的信息。如下图所示,encoder读入输入数据,利用层层叠加的Self-Attention机制对每一个词得到新的考虑了上下文信息的表征。Decoder也利用类似的Self-Attention机制,但它不仅仅看之前产生的输出的文字,而且还要attend encoder的输出。以上步骤如下动图所示:

注:Multi-head Attention其实就是多个Self-Attention结构的结合,每个head学习到在不同表示空间中的特征,如下图所示,两个head学习到的Attention侧重点可能略有不同,这样给了模型更大的容量
详解:
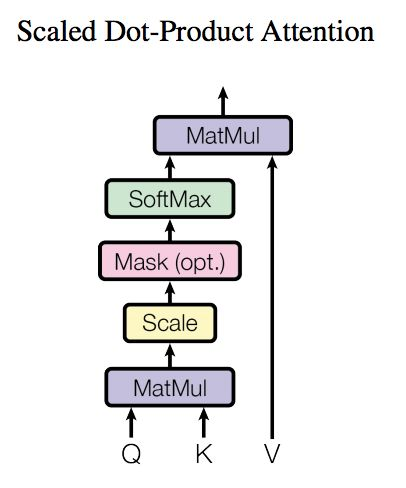
1. 对于self-attention来讲,Q(Query), K(Key), V(Value)三个矩阵均来自同一输入,首先我们将QK矩阵相乘,然后为了防止其结果过大,起到了缩放的作用,会除以一个尺度标度 ,其中
为一个query和key向量的维度。再利用Softmax操作将其结果归一化为概率分布,然后再乘以矩阵V就得到权重求和的表示。该操作可以表示为
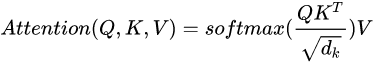
2. mask,在Q*KT后shape是[batch_size, Q, K]
1). 先进行key的mask,相当于找出key的padding,让它softmax后的概率为0,在计算context vector的时候,让其贡献为0
a. 先对key的最后一个维度的每一个值进行绝对值,然后再求和,如果词向量全部是0的话,那么和出来就全部是0,就说明这个时间是padding来的,shape是[batch_size, K]
b. 然后扩展第二个维度,shape是[batch_size, 1, K]
c. 然后进行复制,复制Q次,因为是query的key,有query的长度,shape[batch_size, Q, K]
d. 定义一个极小值,这个值得目的是让softmax后的值为0
e. 最后让mask映射到input里面,为0的部分就为极小值,不为0的部分就为原来的值;这里的意思是,让key中pad的部分在softmax后为0,所以放置极小值
f. 代码:
padding_num = -2 ** 32 + 1
if type in ("k", "key", "keys"):
# Generate masks
a = queries.get_shape().as_list()
masks = tf.sign(tf.reduce_sum(tf.abs(keys), axis=-1)) # (N, T_k)
masks = tf.expand_dims(masks, 1) # (N, 1, T_k)
masks = tf.tile(masks, [1, tf.shape(queries)[1], 1]) # (N, T_q, T_k)
# Apply masks to inputs
paddings = tf.ones_like(inputs) * padding_num
outputs = tf.where(tf.equal(masks, 0), paddings, inputs) # (N, T_q, T_k)
2). 对未来信息进行mask,让self attention的时候看不到未来的词,即在计算context vector的时候,未来的词的概率为0,对计算context vector的贡献为0,这个只在transformer decoder端使用
a. 因为每个时刻只能看到前面的信息,所以这里就使用下三角矩阵,即下三角为1,上三角为0,shape[batch_size, Q, K],每个batch里面的下三角矩阵都是一样的
b. 定义一个极小的值,目的是让softmax后的值为0
c. 然后进行映射,让上三角为0的全部为极小值,下三角的值为原来的值
d. 代码:
padding_num = -2 ** 32 + 1 elif type in ("f", "future", "right"): diag_vals = tf.ones_like(inputs[0, :, :]) # (T_q, T_k) tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense() # (T_q, T_k) masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(inputs)[0], 1, 1]) # (N, T_q, T_k) paddings = tf.ones_like(masks) * padding_num outputs = tf.where(tf.equal(masks, 0), paddings, inputs)
3). 对query进行mask,让query中的padding,在计算context vector的时候为0,即要让query padding部分的时间步骤对K的attention全部为0,这样在计算context vector后才能为0
a. 先对query的最后一个维度的每一个值进行绝对值,然后再求和,如果词向量全部是0的话,那么和出来就全部是0,就说明这个时间是padding来的,shape是[batch_size, Q]
b. 对最后一个维度进行扩展,shape是[batch_size, Q, 1]
c. 是用query去attention key,而key有K个时间步骤,所有要对最后一个时间步骤复制K次,如果原来求出来为0,那么复制出来的值也为0。shape是[batch_size, Q, K],
d. 这个时候求出来的值每行中的值都相等。再乘以input,这里是进行点乘;这里为什么不乘以1,我的理解是相当于乘以了一个常数,即query的每个时间步骤乘以了它自己本身。
e. 代码:
# Generate masks masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1)) # (N, T_q) masks = tf.expand_dims(masks, -1) # (N, T_q, 1) masks = tf.tile(masks, [1, 1, tf.shape(keys)[1]]) # (N, T_q, T_k) # Apply masks to inputs outputs = inputs*masks
4). softmax:这里涉及到多头,我的理解是将多头分开,分开以后有[num_heads, batch_size, Q, K],然后进行矩阵相加[batch_size, Q, K],然后再进行softmax
3. 将最后的attention乘以 V,得到的shape是[batch_size, Q, emdedding_size]
4. 将多头context vector进行复原,例,原来如果词向量是embedding,切分为8个头,那么就是[N*8, Q, embedding/8],attention后,再还原就是[N, Q,embedding]
Hierarchical Attention Networks for Document Classification
这里相当于是self attention,在transformer的self attention里面求的是所有的词对当前词的贡献度,而在这个里面是求的当前词对这段sequence的贡献度
这里只对词级别的attention为例进行说明
1. 将输入进行embedding,shape是[batch_size * num_sentences, sequence, embedding]
2. 将embedding输入到双向LSTM或者GRU,并将输出(不是隐藏层状态)进行拼接, 得到的shape是[batch_size * num_sequence, sequence, output_size * 2]
3. 将上面得到的输出进行一个全连接网络,并用tanh进行激活,得到的shape是[batch_size * num_sequence, sequence, output_size * 2]
4. 将上面得到的输出进行点乘一个context vector,这个context vector是预定义的,shape是[output_size * 2],可以用于训练,目的是衡量哪些词比较重要,得到的shape是[batch_size * num_sequence, sequence, output_size * 2]
5. 将上面得到的输出进行在最后一个维度求和,得到的shape是[batch_size * num_sequence, sequence]。
6. 进行softmax,进行mask,然后再进行re_normal,具体可以参考pointer-genertor中的mask。得到的是每个词对于这个sequence的贡献度,这里就是attention的值, shape是batch_size * num_sequence, sequence]
7. 再将上面得到的结果与双向LSTM或GRU输出的进行一个点乘,得到的结果是[batch_size * num_sequence, sequence, output_size * 2]
8. 在将上面得到的结果进行在第一个维度的相加,得到的就是这个sequence的context vector
稀疏Attention
在上面描述到的都是标准的Self Attention。
优点:能够直接捕捉X中任意两个向量的关联,而且易于并行
缺点:从理论上来讲,Self Attention的计算时间和显存占用量都是O(n2)级别的(n是序列长度),这就意味着如果序列长度变成原来的2倍,显存占用量就是原来的4倍,计算时间也是原来的4倍。当然,假设并行核心数足够多的情况下,计算时间未必会增加到原来的4倍,但是显存的4倍却是实实在在的,无可避免,这也是微调Bert的时候时不时就来个OOM的原因了。因为它要对序列中的任意两个向量都要计算相似度,得到n2大小的相关度矩阵
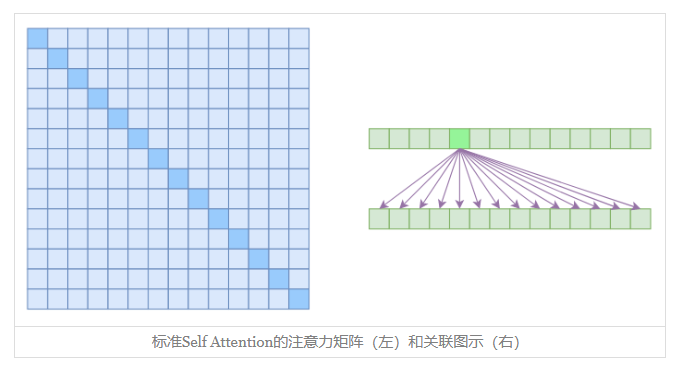
从上面缺点来看,如果要减少关联性的计算,也就是认为每个元素只跟序列内的一部分元素有关,这就是稀疏Attention的基本原理。
Atrous Self Attention
第一个要引入的概念是Atrous Self Attention,中文可以称之为“膨胀自注意力”、“空洞自注意力”、“带孔自注意力”等。
很显然,Atrous Self Attention就是启发于“膨胀卷积(Atrous Convolution)”,如下右图所示,它对相关性进行了约束,强行要求每个元素只跟它相对距离为k,2k,3k,…的元素关联,其中k>1是预先设定的超参数。从下左的注意力矩阵看,就是强行要求相对距离不是k的倍数的注意力为0(白色代表0):
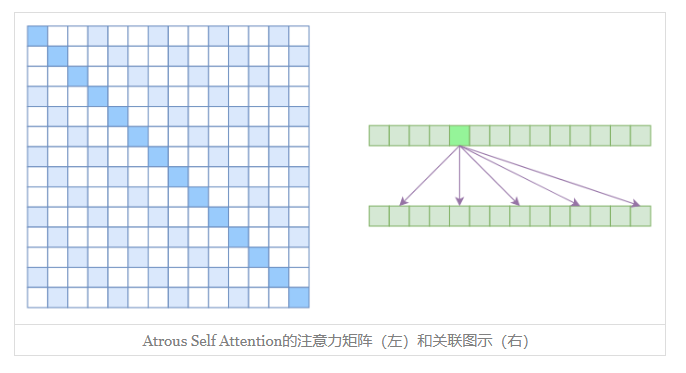
由于现在计算注意力是“跳着”来了,所以实际上每个元素只跟大约 n / k 个元素计算相关性,这样一来理想情况下运行效率和显存占用都变成了O(n2/k),也就是说能直接降低到原来的1/k
Local Self Attention
另一个要引入的过渡概念是Local Self Attention,中文可称之为“局部自注意力”。其实自注意力机制在CV领域统称为“Non Local”,而显然Local Self Attention则要放弃全局关联,重新引入局部关联。具体来说也很简单,就是约束每个元素只与前后k个元素以及自身有关联,如下图所示:
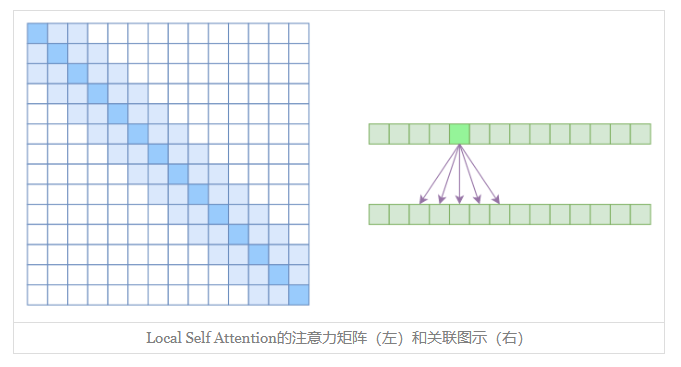
从注意力矩阵来看,就是相对距离超过kk的注意力都直接设为0。
都是保留了一个2k+1大小的窗口,然后在窗口内进行一些运算,不同的是普通卷积是把窗口展平然后接一个全连接层得到输出,而现在是窗口内通过注意力来加权平均得到输出。对于Local Self Attention来说,每个元素只跟2k+1个元素算相关性,这样一来理想情况下运行效率和显存占用都变成了O((2k+1)n)∼O(kn),也就是说随着nn而线性增长,这是一个很理想的性质——当然也直接牺牲了长程关联性。
Sparse Self Attention
到此,就可以很自然地引入OpenAI的Sparse Self Attention了。我们留意到,Atrous Self Attention是带有一些洞的,而Local Self Attention正好填补了这些洞,所以一个简单的方式就是将Local Self Attention和Atrous Self Attention交替使用,两者累积起来,理论上也可以学习到全局关联性,也省了显存。
例:输入的向量进行两个Attention,一个是Local Self Attention, 那么输出的向量都融合了局部的相联特征,然后第二层用 Atrous Self Attention,虽然它是跳着来,但是因为第一层的输出融合了局部的输入向量,所以第二层的输出理论可以跟任意的输入向量相关(因为的空洞为k,而k中的每个元素经过了2k+1的局部,所以相当于和任意输入关联),也就是说实现了长程关联。
但是OpenAI没有这样做,它直接将两个Atrous Self Attention和Local Self Attention合并为一个,如
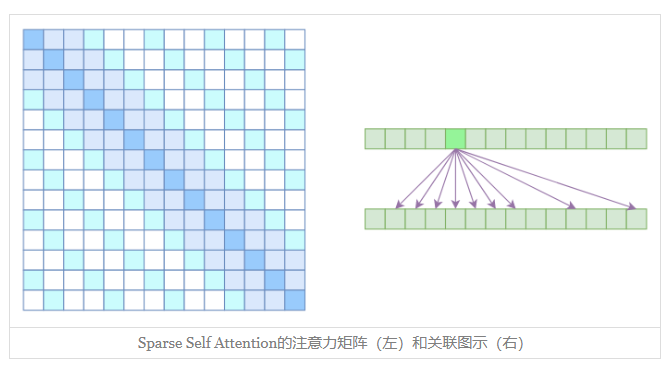
从注意力矩阵上看就很容易理解了,就是除了相对距离不超过k的、相对距离为k,2k,3k,…的注意力都设为0,这样一来Attention就具有“局部紧密相关和远程稀疏相关”的特性,这对很多任务来说可能是一个不错的先验,因为真正需要密集的长程关联的任务事实上是很少的。