矩阵

正交
如果向量空间中两个向量的內积为0，则他们正交。如果向量空间中的一个向量v与子空间u中的每个向量都正交，那么向量y和子空间u正交。

范数
一个表示向量“长度”的函数，为向量空间的所有向量赋予非零的正长度或大小。对于一个n维向量v，一个常见的范数函数为：

 

ℓ1 范数ℓ1 范数为向量的各个元素的绝对值之和。

ℓ2 范数ℓ2 范数为向量的各个元素的平方和再开平方。

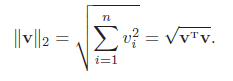
ℓ2 范数又称为Euclidean 范数或者Frobenius 范数。从几何角度，向量也可以表示为从原点出发的一个带箭头的有向线段，其ℓ2 范数为线段的长度，也常称为向量的模。

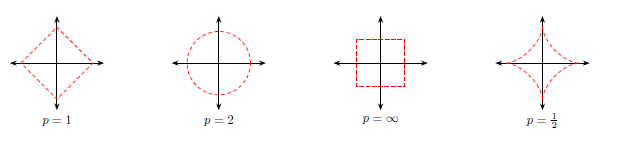
ℓ∞ 范数ℓ∞ 范数为向量的各个元素的最大绝对值

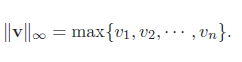
常见的范数示例：

矩阵乘法

矩阵的乘法满足结合律和分配律：

　　• 结合律：(AB)C = A(BC),
　　• 分配律：(A + B)C = AC + BC，C(A + B) = CA + CB.

 

迹

方块矩阵A的对角线元素之和称为它的迹（Trace），记为tr(A)。尽管矩阵的乘法不满足交换律，但它们的迹相同，即tr(AB) = tr(BA)。

 

行列式

方块矩阵A的行列式是一个将其映射到标量的函数，记作det(A) 或|A|。行列式可以看做是有向面积或体积的概念在欧氏空间中的推广。在n 维欧氏空间中，行列式描述的是一个线性变换对“体积”所造成的影响。

计算方法：取自不同行不同列的n个元素的乘机之和，n为阶数。在n个元素相乘时要乘以sgn(σ)，sgn(σ)定义为：

这里的逆序是指元素的下标，如A_ij，比较的是i和j的大小。

 

对称矩阵

对称矩阵（Symmetric Matrix）指其转置等于自己的矩阵，即满足A = A^T。

 

对角矩阵

对角矩阵（Diagonal Matrix）是一个主对角线之外的元素皆为0 的矩阵。对角线上的元素可以为0 或其他值。一个n × n的对角矩阵A满足：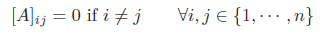

　　对角矩阵A也可以记为diag(a)，a 为一个n维向量，并满足

 

　　n × n的对角矩阵A = diag(a) 和n维向量b的乘积为一个n维向量

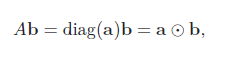
其中⊙表示点乘，即(a ⊙ b)_i = a_ib_i。

 

单位矩阵

单位矩阵（Identity Matrix）是一种特殊的的对角矩阵，其主对角线元素为1，其余元素为0。n 阶单位矩阵In，是一个n × n 的方块矩阵。可以记为In = diag(1, 1, ..., 1)。

　　一个m × n的矩阵A和单位矩阵的乘积等于其本身。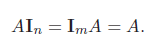

逆矩阵

对于一个n × n的方块矩阵A，如果存在另一个方块矩阵B 使得

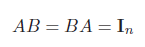
为单位阵，则称A是可逆的。矩阵B 称为矩阵A的逆矩阵（Inverse Matrix），记为A⁻¹。一个方阵的行列式等于0 当且仅当该方阵不可逆。

 

正定矩阵

对于一个n × n 的对称矩阵A，如果对于所有的非零向量x ∈ Rⁿ都满足

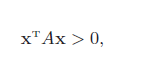
则A为正定矩阵（Positive-Definite Matrix）。如果x^TAx ≥ 0，则A是半正定矩阵（Positive-Semidefinite Matrix）。

 

正交矩阵

正交矩阵（Orthogonal Matrix ）A为一个方块矩阵，其逆矩阵等于其转置矩阵。

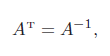
等价于A^TA = AA^T = I_n。

 

Gram 矩阵

向量空间中一组向量v₁, v₂ · · · , v_n 的Gram 矩阵（Gram Matrix）G是内积的对称矩阵，其元素Gij 为v^T_i v_j。

 

特征值与特征矢量

如果一个标量λ 和一个非零向量v满足

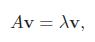
则λ 和v分别称为矩阵A的特征值（Eigenvalue）和特征向量（Eigenvector）。

 

奇异值分解

一个m×n的矩阵A的奇异值分解（Singular Value Decomposition，SVD）定义为

其中U 和V 分别为m × m和n × n 的正交矩阵，Σ为m × n 的对角矩阵，其对角线上的元素称为奇异值（Singular Value）。

 

特征分解

一个n × n的方块矩阵A的特征分解（Eigendecomposition）定义为

 

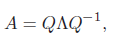
其中Q为n×n的方块矩阵，其每一列都为A的特征向量，Λ为对角阵，其每一个对角元素为A的特征值。

　　如果A为对称矩阵，则A可以被分解为

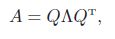
其中Q为正交阵。