空洞卷积-膨胀卷积

在图像分割领域，图像输入到CNN，FCN先像传统的CNN那样对图像做卷积再pooling，降低图像尺寸的同时增大感受野，但是由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测，之前的pooling操作使得每个pixel预测都能看到较大感受野信息。因此图像分割FCN中有两个关键，一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中，内部数据结构丢失；空间层级化信息丢失。小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)，在这样问题的存在下，语义分割问题一直处在瓶颈期无法再明显提高精度， 而 dilated convolution 的设计就良好的避免了这些问题。

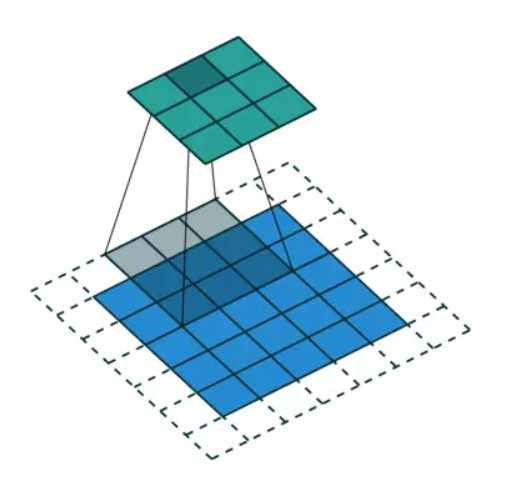
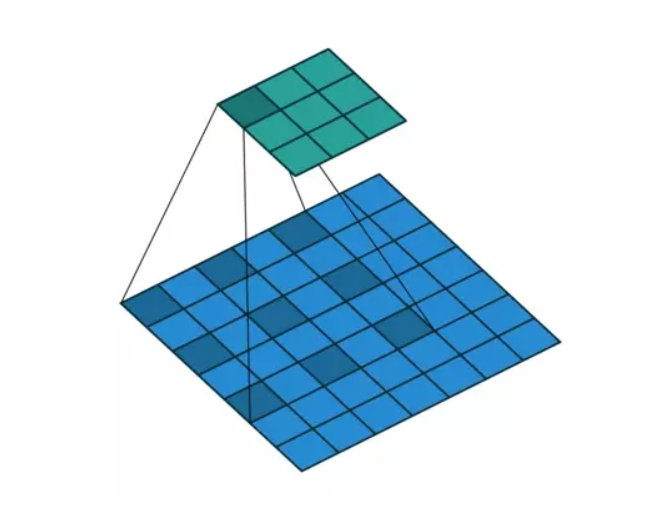
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (a)　　　　　　　　　　　　　　　　　　　　   (b)

 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 

(a). 图对应3x3的1-dilated conv，和普通的卷积操作一样

(b). 图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个5x6的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为5x5，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3x3，但是这个卷积的感受野已经增大 到了5x5

 

好处： 

1. dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。

2. 在赢得其中一届ImageNet比赛里VGG网络的文章中，他最大的贡献并不是VGG网络本身，而是他对于卷积叠加的一个巧妙观察。

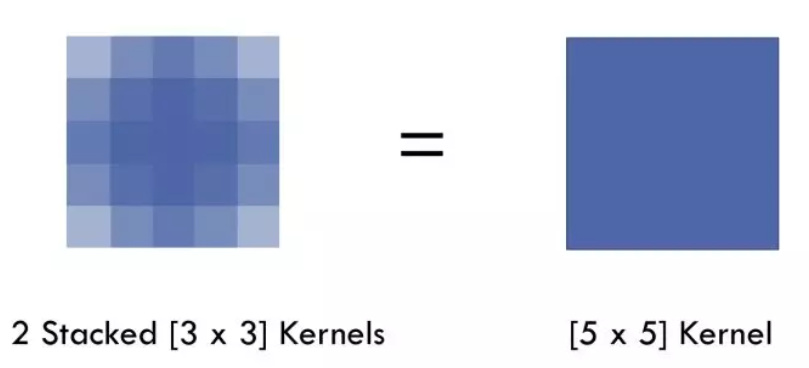
This (stack of three 3 × 3 conv layers) can be seen as imposing a regularisation on the 7 × 7 conv. filters, forcing them to have a decomposition through the 3 × 3 filters (with non-linearity injected in between).

3.  这里意思是 7 x 7 的卷积层的正则等效于 3 个 3 x 3 的卷积层的叠加。而这样的设计不仅可以大幅度的减少参数，其本身带有正则性质的 convolution map 能够更容易学一个 generlisable, expressive feature space。这也是现在绝大部分基于卷积的深层网络都在用小卷积核的原因。

 

潜在问题：

假设我们仅仅多次叠加 dilation rate 2 的 3 x 3 kernel 的话，则会出现这个问题：

我们发现我们的 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。