快速傅里叶（FFT）的快速深度思考
关于按时间抽取快速傅里叶（FFT）的快速理论深度思考
对于FFT基本理论参考维基百科或百度百科。
首先谈谈FFT的快速何来？大家都知道FFT是对DFT的改进变换而来，那么它究竟怎样改进，它改进的思想在何处呢？明白后，深感奇妙，感悟学习，感悟生活，写下此文，供大家分享之。（文中FFT均讨论按时间抽取快速傅里叶（FFT））
首先我们来一起看看变换公式，DFT ->FFT（整数 ->奇数 + 偶数）
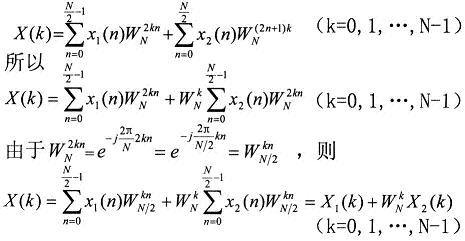
我自己到这结束也没了解它是怎么把时间变少的，从O(N2)(DFT时间深度）到O(N log2 N)(FFT时间深度)，智商无能望见谅……
那么我就画了下四点为例的流程图，如下：
FFT四点流图
DFT四点流图
对比DFT和FFT的流图，思考了半天我才醒悟，原来关键词是“中间变量”。
何解？FFT产生了中间变量来得到最后的结果，而DFT直接全部计算得出结果。那么从流图中我们可以发现，FFT对产生的中间变量进行多次引用，也就是说中间变量只算了一次，而被反复利用多次，举个不恰当的例子：“1 + 1 + 1 = 3”,"1 + 1 = 2 ,2 + 1 = 3"这两个结果一样，但是过程2中的中间变量“2”还可以用在“2 + 2 =4”的算式中。这就是关键。所以对于数量级大的计算来说产生中间变量的好处就是避免了对于中间变量的重复运算，使运算过程加快。
对于流图我们发现四点FFT和DFT的运算一样多，都是16条线，那么8点的流图你就会轻易发现运算量就不同了：
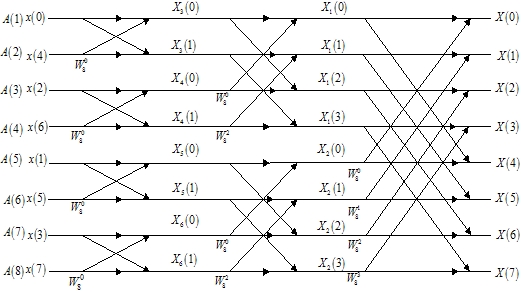
FFT:8*3*2 = 48 条，DFT：8*8 = 64 条。对于更大数量级，效果就更明显了。回头看变换式，也能清晰看到在第一、二步：分奇偶，没有任何优化；最后一步：我们就可以看到优化过程：产生了中间变量。
反复思考：其实在DFT中我们也会计算得到相同结果，说明我们做了相同工作，所以我们工作量是一样的，只是我们把像FFT那样产生的中间变量多次计算，就像我上面举的例子，你把“1 + 1 =2”多次计算了，而这个明明已经算过了的，这就是我们的时间消耗点。
那么回头全局观察总结一下：我们在计算一个共同结果或完成一个共同的长远目标时，我们最好是分成多步完成。（这就是我最想说的一个从中悟到的思维问题。因为我探究这问题就是从“想弄明白为‘啥就能加速’，这个神奇的思维是什么”开始的，产生“中间变量”）。而且我信奉思维构造上层建筑，所以我很关注一些问题解决的本质思维问题，这个问题也是最近学FFT突然想到的，希望大家能和我一起学习交流，恳求您的悉心教导。
反观生活：其实我们发现我们点的“科技树”就是这样；我们写的API，写的库函数就是这样。它们都是这个思维的引用者，确实加快了速度，不是吗！
突发奇想：我以前准备举个多元化的例子，发现不行，不符合。这个例子是“一双鞋，鞋带中国制造，鞋底巴西，鞋上层美国”（此例胡说的，博主不懂具体，只是高中政治书回忆起的），这个例子的分步，但是并不是串行，是并行结构，这个方法的前提就是各部分大家都知道目标和底层运行过程，不知道有什么算法可以和这个思想一样。博主写到这自己发现说糊涂了，晕了，大家见谅着看吧，抱歉- - 。
