Kruskal 重构树学习笔记+杂题
图论系列：
前言：
相关题单：戳我
一.最小瓶颈路
唉，前面4个题单里其实有不少题是最小瓶颈路的做法啊。讲解摘自 wiki 。
1.定义
无向图 \(G\) 中 \(x\) 到 \(y\) 的最小瓶颈路是这样的一类简单路径，满足这条路径上的最大的边权在所有 \(x\) 到 \(y\) 的简单路径中是最小的。（对于下面这张图， \(2 \to 3\) 的最小瓶颈路就是 \(2 \to 1 \to 5 \to 3\) ，此时经过路径最大值为 \(4\)）。
相当于你需要一定的等级才能走一条边（这就是边权），问你需要从 \(x\) 走到 \(y\) 所需要的最小等级。将所有小于等于此等级的边添加如图中，图中每一条 \(x \to y\) 的路径都是最小瓶颈路。
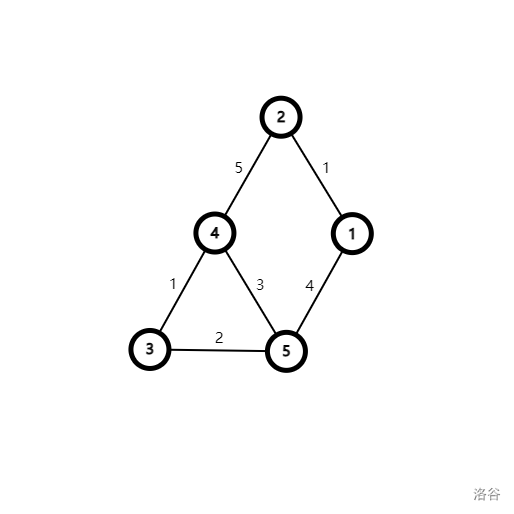
2.性质
根据最小生成树定义，\(x\) 到 \(y\) 的最小瓶颈路上的最大边权等于最小生成树上 \(x\) 到 \(y\) 路径上的最大边权。虽然最小生成树不唯一，但是每种最小生成树 \(x\) 到 \(y\) 路径的最大边权相同且为最小值。也就是说，每种最小生成树上的 \(x\) 到 \(y\) 的路径均为最小瓶颈路。
但是，并不是所有最小瓶颈路都存在一棵最小生成树满足其为树上 \(x\) 到 \(y\) 的简单路径。
3.应用
由于最小瓶颈路不唯一（如上图中最小瓶颈路还可以是 \(2 \to1 \to 5\to 4 \to 3\) ），一般情况下会询问最小瓶颈路上的最大边权。也就是说，我们需要求最小生成树链上的 max，倍增、树剖都可以解决。
给一道板子题，先将最小生成树建出来后判断链上边权最大值即可（注意可能最后图可能不连通，可能会生成一个最小生成树森林）。
代码：
//采用的是树剖+倍增求解
const int M=1e3+5,N=1e5+5;
int n,m,q;
int fax[M],vis[M],deep[M],fa[M][19],dis[M][19];
struct node{
int u,v,w;
inline bool operator <(const node o) const
{
return w<o.w;
}
};node e[N];
int cnt=0;
struct Edge{
int to,next,val;
};Edge p[N<<1];
int head[M];
inline void add(int a,int b,int c)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
p[cnt].val=c;
}
inline int find(int x)
{
if(x!=fax[x]) fax[x]=find(fax[x]);
return fax[x];
}
inline void dfs(int u,int f)
{
fa[u][0]=f,deep[u]=deep[f]+1,vis[u]=1;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dis[v][0]=p[i].val;
dfs(v,u);
}
}
inline int lca(int x,int y)
{
if(deep[x]<deep[y]) swap(x,y);
int c=deep[x]-deep[y],res=0;
for(int i=0;i<=18;++i)
{
if(c&(1<<i)) res=max(res,dis[x][i]),x=fa[x][i];
}
for(int i=18;i>=0;--i)
{
if(fa[x][i]!=fa[y][i])
{
res=max(res,max(dis[x][i],dis[y][i]));
x=fa[x][i],y=fa[y][i];
}
}
if(x==y) return res;
res=max(res,max(dis[x][0],dis[y][0]));
return res;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=n;++i) fax[i]=i;
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
fax[x]=y;
add(e[i].u,e[i].v,e[i].w),add(e[i].v,e[i].u,e[i].w);
}
for(int i=1;i<=n;++i) if(!vis[i]) dfs(i,0);
for(int j=1;j<=18;++j)
{
for(int i=1;i<=n;++i)
{
fa[i][j]=fa[fa[i][j-1]][j-1];
dis[i][j]=max(dis[i][j-1],dis[fa[i][j-1]][j-1]);
}
}//倍增处理
int x,y;
while(q--)
{
cin>>x>>y;
if(find(x)!=find(y)) cout<<"-1\n";
else cout<<lca(x,y)<<"\n";
}
return 0;
}
二.Kruskal 重构树
1.定义：
我呃呃，这没定义啊，直接说建树过程吧。（一开始是用来解决最小瓶颈路的吧）。
对于一张无向图有 \(n\) 个点，边有边权，那么按照 Kruskal 求最小生成树的过程，将边权从小到大的加入图中，用并查集判断连接的两点是否连通（当然就是把根找出来了），如果不连通便跳过，否则建一个新点，让这个新点连向找到的两个根，然后这两个根同新建的点合并（完成了使连接的两个连通块连通的过程），同时将新点的点权赋为当前连的边的边权（原先的 \(n\) 个点边权设为 \(0\)）。
如果图是无向连通图的话，最后就会生成一棵树，这个树我们称之为 Kruskal 重构树。（当然 Kruskal 重构树 有两种，一种就是这样按最小生成树建，还有一种是按最大生成树建）。
2.过程
直接说不是很直观，对于下面一张图，考虑建其最小生成树的 Kruskal 重构树 。
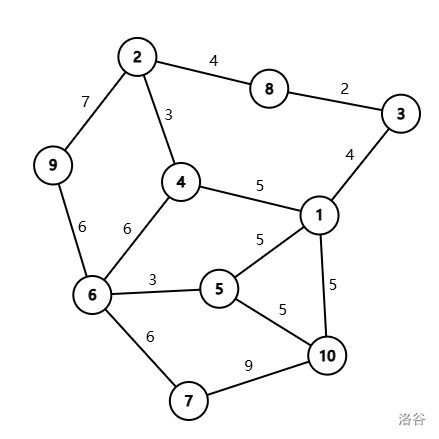
下面就是这张图的最小生成树其中之一（不唯一，红色的就是最小生成树的树边）。
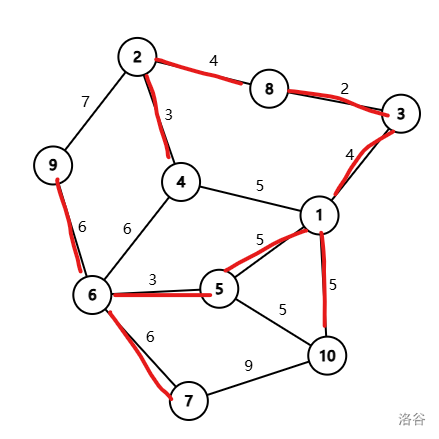
首先先将边权为 \(2\) 与边权为 \(3\) 的边加进去（可以看出，合并的时候都是强制让当前新建的这个点成为两个根的根，红色标的值就是当前点的点权，没标的叶子节点点权默认为 \(0\) ）。
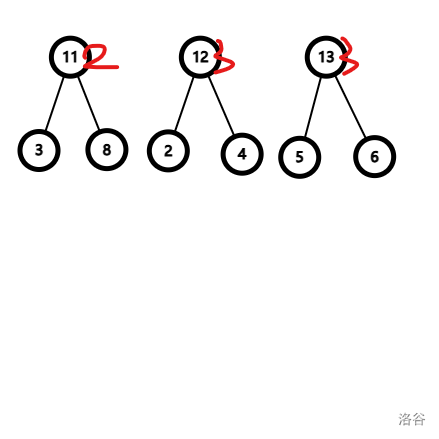
然后从小到大加入边权为 \(4\) 的边。
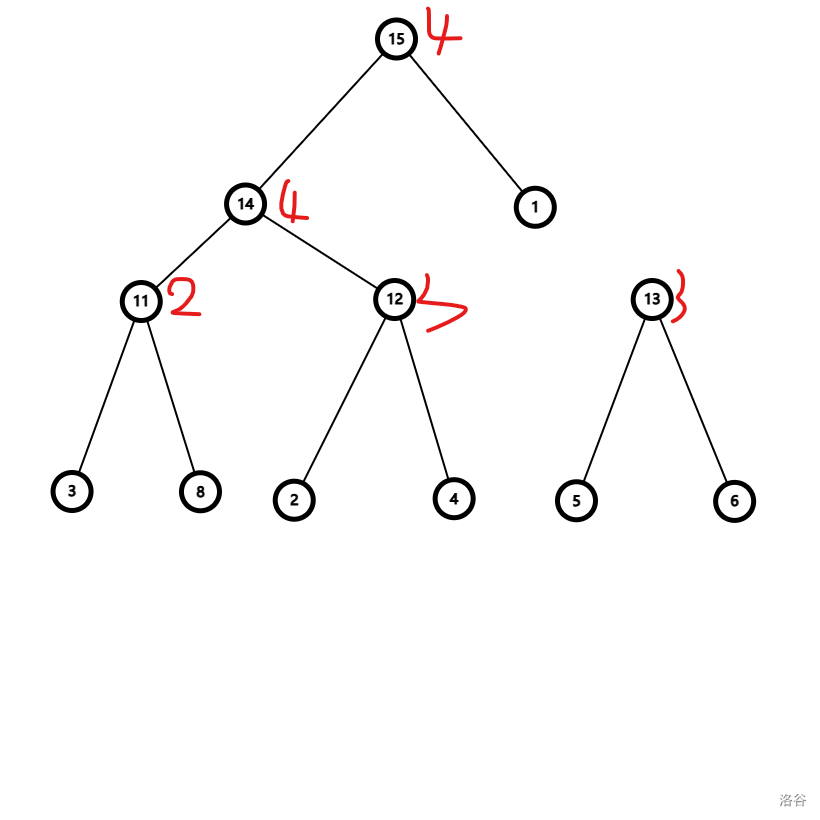
加入边权为 \(5\) 的边。
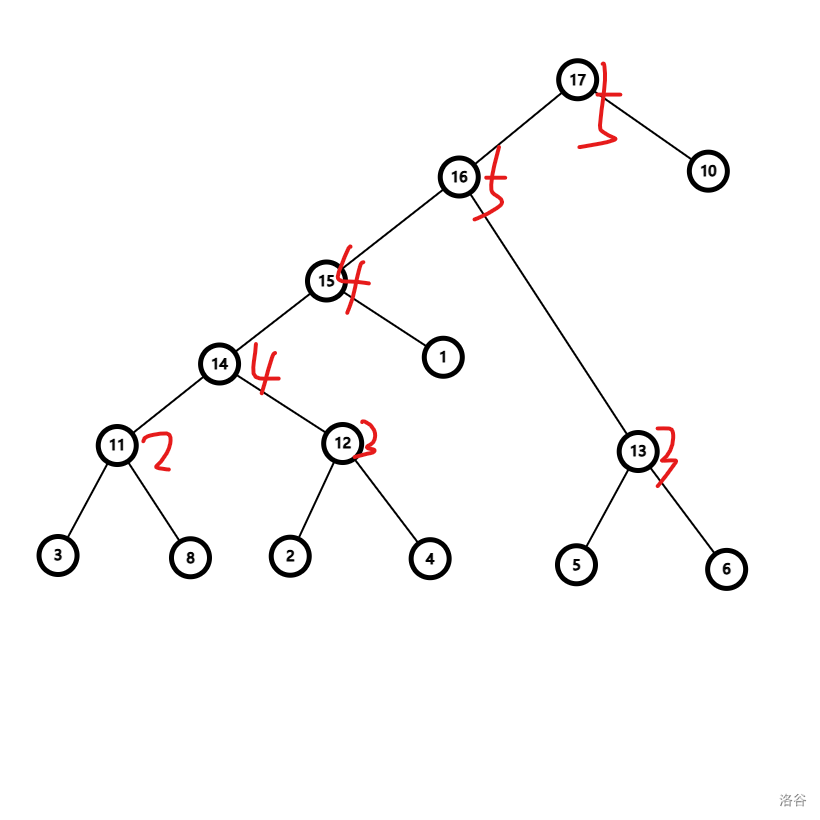
加入边权为 \(6\) 的边。
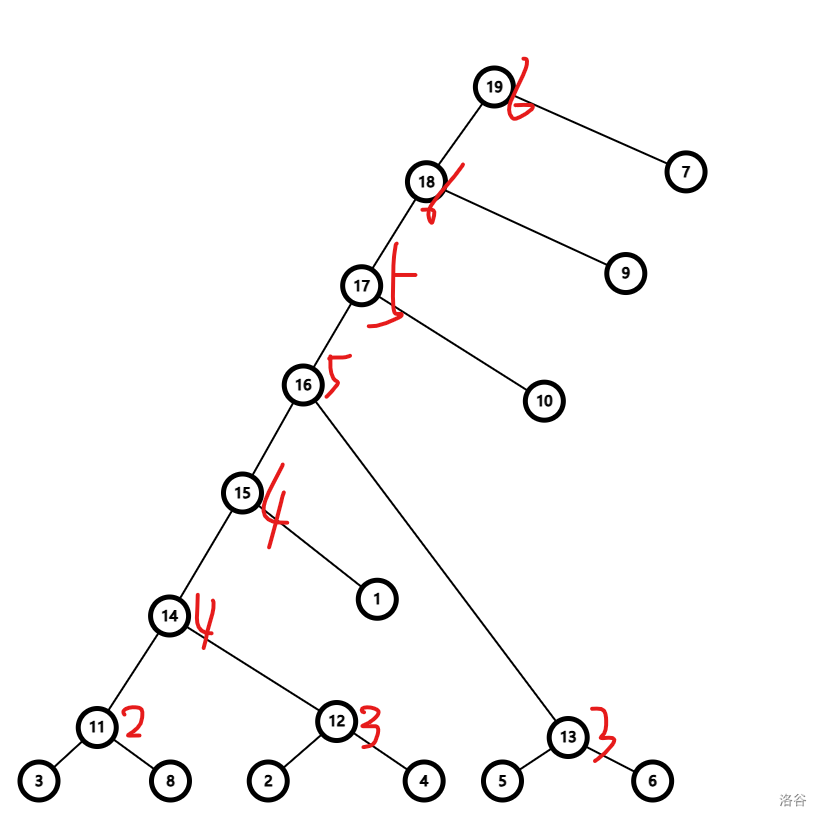
非常直观了吧，这就是建树的过程。
3.性质
这里给定最小生成树 Kruskal 重构树 的性质，那么最大生成树 Kruskal 重构树 的性质可以同理得。
重构树是一棵恰有 \(n\) 个叶子节点的完满二叉树，每个非叶子节点都有两个儿子，共有 \(2n-1\) 个点。（初始图中的 \(n\) 个点是叶子，由于是棵树，边数为 \(n-1\) ，相当于每条边都新建了一个点，那么点数自然是 \(2n-1\) ）。
重构树的点权符合大根堆的性质。（从上到下边权递减，最上面的点边权最大，因为边权大的边后面加）。
原图中两点间所有简单路径的最大边权最小值，等于最小生成树上两点之间边权最大值，等于重构树上两点 LCA 的点权。（这下任意两点间的最小瓶颈路就只用求一个 LCA 了）。
从 \(u\) 出发，经过边权不超过 \(k\) 的边，所能到达的点恰好是重构树上某棵子树内的所有叶子节点。（可以这么想，从 \(u\) 点一直向上走，直到点权大于 \(k\)，那么那个点相当于就不能过，由于是一颗树，不能经过一个点，断开之后 \(u\) 所在部分就是一颗子树）。
4.习题
某些习题需要掌握一定的数据结构知识。（md，有时候学算法，啥也不会，dfs回去都快爆栈了），所以有很多鸽子题。
P1967 [NOIP2013 提高组] 货车运输
实际上就是上面那道最小瓶颈路模板题的双倍经验了，但是这里我们采用 Kruskal 重构树解决，模板题讲解都放在代码上。
需要注意的是，这道题给定的边权是限重（重量总不能超过限重吧），所以一条路径的权值就可以看作是边权的最小值，现在要求的就是所有路径权值的最大值，刚好反过来了，所以我们采用最大生成树 的 Kruskal 重构树
代码：
const int M=1e5+5;
int n,m,q,tot;
int w[M],F[M];
int cnt=0;
struct N{
int to,next;
};N p[M];
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w>o.w;
}
};edge e[M];//最大生成树，边权从大到小
int head[M];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int siz[M],fa[M],son[M],deep[M];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int top[M];
inline void dfs2(int u,int topp)
{
top[u]=topp;
if(!son[u]) return ;
dfs2(son[u],topp);
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(top[v]) continue;
dfs2(v,v);
}
}
inline int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(deep[x]>deep[y]) return y;
return x;
}//树链剖分+LCA
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m,tot=n;//虚点从n+1开始建
for(int i=1;i<=(n<<1);++i) F[i]=i;//初始化2倍空间，最后有2*n-1个点
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)//建最大生成树的同时将重构树建出来
{
x=find(e[i].u),y=find(e[i].v);//查找当前集合的根
if(x==y) continue;
++tot;//这条边在最大生成树上，建新虚点
F[x]=tot,F[y]=tot,w[tot]=e[i].w;//强制让虚点成为 x,y 两个根的根，边权转为点权
add(tot,x),add(tot,y);//建树
}
for(int i=tot;i>n;--i) if(!siz[i]) dfs1(i,0,1);//还有一点需要注意，根只有可能是大于 n 的点，且越后加的点越有可能是根，所以从后向前遍历每个点，看其是否为根（这很重要，否则随便选个点做根，重构树就没有各种优秀的性质了）
for(int i=tot;i>n;--i) if(!top[i]) dfs2(i,i);
//题目中没有保证给定的是一颗无向连通图，所以可能建出来一个森林
cin>>q;int x,y;
while(q--)
{
cin>>x>>y;
if(find(x)!=find(y)) {cout<<"-1\n";continue;}//两点都不连通，没法到达
cout<<w[lca(x,y)]<<"\n";//那么两点路径最大权值就是在最大生成树建出的 Kruskal 重构树上两点的LCA的点权
}
return 0;
}
P2245 星际导航
同样是板子题，这题的路径权值为边权的最大值，询问我们路径的最小值，于是考虑建最小生成树的 Kruskal 重构树。那么将上道题代码 copy 下来，边排序顺序变一下，两点不连通输出 impossible 就可以过了。
代码：
const int M=3e5+5;
int n,m,q,tot;
int w[M],F[M];
int cnt=0;
struct N{
int to,next;
};N p[M];
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w<o.w;
}
};edge e[M];
int head[M];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int siz[M],fa[M],son[M],deep[M];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int top[M];
inline void dfs2(int u,int topp)
{
top[u]=topp;
if(!son[u]) return ;
dfs2(son[u],topp);
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(top[v]) continue;
dfs2(v,v);
}
}
inline int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(deep[x]>deep[y]) return y;
return x;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m,tot=n;
for(int i=1;i<=(n<<1);++i) F[i]=i;
for(int i=1;i<=m;++i)
{
cin>>e[i].u>>e[i].v>>e[i].w;
}
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot;
F[x]=tot,F[y]=tot,w[tot]=e[i].w;
add(tot,x),add(tot,y);
}
for(int i=tot;i>n;--i) if(!siz[i]) dfs1(i,0,1);
for(int i=tot;i>n;--i) if(!top[i]) dfs2(i,i);
cin>>q;int x,y;
while(q--)
{
cin>>x>>y;
if(find(x)!=find(y)) {cout<<"impossible\n";continue;}
cout<<w[lca(x,y)]<<"\n";
}
return 0;
}
CF1706E Qpwoeirut and Vertices
好题。给出 \(n\) 个点， \(m\) 条边的不带权连通无向图， \(q\) 次询问至少要加完编号前多少的边，才能使得 \([l,r]\) 中的所有点两两连通。
需要转化的一道题，首先由于询问的是加完编号前多少的边，那么我们可以将每条边的边权赋为它出现的编号，第 \(i\) 条边的边权就是 \(i\)，那么先考虑两个点，要这两个点连通需要让编号前多少的边加入？此时，一条路径的权值就是路径上边的边权最大值，然后我们要求路径的权值最小，那么这不就是一个最小生成树 Kruskal 重构树 板子题了。
将两个点的思路拓展为一个区间 \([l,r]\) 内所有的点，自然就是求区间内所有点共同的 LCA 。解决这个问题，想到一个对于树的经典的trick：对于多个点求 LCA，这个 LCA 就是给定的多个点中 dfn 序最小的的那个点与 dfn 序最大的那个点的 LCA 。于是树剖之后每个点会得到一个 dfn 值（因为不同的遍历方法每个点的 dfn 值可能不唯一），现在我们就需要查询 \([l,r]\) 中 dfn 序最小的的那个点与 dfn 序最大的那个点。
相当于就是一个序列，求一个区间内的最小值与最大值（ rmq 问题），这里采用的是 ST 表写法。得到之后，我们肯定在遍历树的时候记录一个 dfn 的映射数组（就是记录某个 dfn 值对应的是哪个点），于是将最小和最大 dfn 值知道后，我们就可以知道这两个点，对这两个点在 Kruskal 重构树上求 LCA，求得的 LCA 的点权就是答案。（整个题的思路还是比较顺的）
代码：
const int M=4e5+5;
int T,n,m,q,tot;
int F[M],w[M],pre[M];
int cnt=0;
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w<o.w;
}
};edge e[M];
struct N{
int to,next;
};N p[M<<1];
int head[M];
inline void add(int a,int b)
{
//cout<<a<<" "<<b<<"\n";
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int fa[M],siz[M],son[M],deep[M];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int dfn[M],id[M],num,top[M];
inline void dfs2(int u,int topp)
{
top[u]=topp,dfn[u]=++num,id[num]=u;
if(!son[u]) return ;
dfs2(son[u],topp);
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(top[v]) continue;
dfs2(v,v);
}
}
inline int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(deep[x]<deep[y]) return x;
return y;
}
int minn[M][20],maxx[M][20];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>T;
for(int i=2;i<M;++i) pre[i]=pre[i/2]+1;
while(T--)
{
cin>>n>>m>>q,tot=n,cnt=num=0;
for(int i=1;i<=2*n;++i) F[i]=i,head[i]=son[i]=top[i]=0;
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v,e[i].w=i;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot;
F[x]=F[y]=tot,w[tot]=e[i].w;
add(tot,x),add(tot,y);
}
dfs1(tot,0,1),dfs2(tot,tot);//保证了连通，ヽ(✿ﾟ▽ﾟ)ノ，根就是最后一个添加的虚点
for(int i=1;i<=n;++i) maxx[i][0]=minn[i][0]=dfn[i];
for(int j=1;j<=19;++j)
{
for(int i=1;i<=n;++i)
{
minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
maxx[i][j]=max(maxx[i][j-1],maxx[i+(1<<(j-1))][j-1]);
}
}//ST表求区间最小/最大值
int l,r,s,x,y;
while(q--)
{
cin>>l>>r,s=pre[r-l+1];
if(l==r) {cout<<"0 ";continue;}
x=id[min(minn[l][s],minn[r-(1<<s)+1][s])];//dfn 最小值对应的点
y=id[max(maxx[l][s],maxx[r-(1<<s)+1][s])];//dfn 最大值对应的点
cout<<w[lca(x,y)]<<" ";
}
cout<<"\n";
}
return 0;
}
CF1578L Labyrinth
分类讨论题，需要借助重构树的性质完成一些贪心的转化，题解讲的都很好ing。（就不班门弄斧了）
代码：
const int M=2e5+5;
int n,m,tot;
int c[M],F[M],sum[M],ans[M];
struct edge{
int u,v,w;
inline bool operator <(const edge o) const
{
return w>o.w;
}
};edge e[M];
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m,tot=n;
for(int i=1;i<=n;++i) cin>>c[i];
for(int i=1;i<=(n<<1);++i) F[i]=i,ans[i]=2e9;
for(int i=1;i<=m;++i)
{
cin>>e[i].u>>e[i].v>>e[i].w;
}
sort(e+1,e+m+1);
for(int i=1,x,y,w;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot;
F[x]=F[y]=tot,w=e[i].w;
c[tot]=c[x]+c[y];
ans[tot]=max(min(w-c[y],ans[y]-ans[x]),min(w-c[x],ans[x]-ans[y]));
}
cout<<(ans[tot]>0?ans[tot]:-1)<<"\n";
return 0;
}
P4768 [NOI2018] 归程
经典老题，覆盖面广，具有启发性，详记一下。
对于这种题先从简单限制开始做。首先先不管车子以及降水的限制，那么就是单独的对于一张图，询问两点的最短路，并且其中一点固定为 \(1\) ，那么这不是单源路径最短问题嘛，注意到边权都是非负数，所以以 \(1\) 为源点跑一遍 dijkstra 求出 \(1\) 到每个点的最短路（这样方便我们查询从某点下车后究竟还要走多久）。
加入车这个条件，如果没有降水的限制，那么答案就为 \(0\)，直接从当前点开到 \(1\) 即可。再加入降水&海拔，观察究竟有什么影响，相当于就是如果降水大于等于某条边的海拔，那么这条边就不能用车走。暴力的做法显然是从起点跑一遍 bfs （不能走的边就不走），得到可以开车从起点到达的点，观察这些点中距离 \(1\) 最小的就是答案了。
但是时间限制显然要求我们不能这么做，那怎么优化？考虑对于车走的一条路径，它的权值相当于路径上边的边权最小值（因为如果海拔最小的那条边被淹了，这条路车就不能走了），显然路径的权值越大越好，此时就是一个最大生成树的 Kruskal 重构树。那我们依据每条边的海拔作为权值建出 Kruskal 重构树。
Kruskal 重构树有什么用？还记得我们说的暴力做法嘛——统计从起点出发用车能到达的点（因为已经求出 \(1\) 到每个点的距离 \(dis_i\)了，知道点之后直接对这些点求一个 \(dis_i\) 的最小值即可）。Kruskal 重构树有什么性质？根据上面性质第二条与第四条，对于最大生成树的 Kruskal 重构树，点权符合小根堆的性质，经过边权不小于 \(k\) 的边，所能到达的点恰好是重构树上某棵子树内的所有叶子节点。
那么我们就可以从当前起点一直在重构树上跳，直到某个祖先点的权值刚好大于等于给定的降水（它的父亲节点权值就小于给定的降水了）。这个祖先点下属的叶子节点就是当前起点在当前降水能到达的所有点了，再在一开始的时候 dfs 预处理一下每个节点下属距离点 \(1\) 最小是多少，那么答案就是这个祖先点处理出来的叶子节点距离点 \(1\) 最小的值。分析一下时间复杂度，跑一次最短路+ dfs 一次+建重构树+跳祖先（当然不能一个一个点的向上跳，需要采用倍增的方法），时间复杂度最高就是 \(O(nlogn)\)，非常优秀。
代码：
const int M=4e5+5;
int T,n,m,q,k,s;
int cnt=0,tot=0;
struct edge{
int u,v,dis;
inline bool operator <(const edge &o) const
{
return dis>o.dis;
}
};edge e[M];
struct N{
int to,next,val;
};N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b,p[cnt].val=c;
}
int dis[M],vis[M];
inline void dijkstra(int u)
{
memset(vis,0,sizeof(vis)),memset(dis,0x3f,sizeof(dis));
priority_queue<pii,vector<pii>,greater<pii>> q;
dis[u]=0,q.push(mk(0,1));
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to,w=p[i].val;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
if(!vis[v]) q.push(mk(dis[v],v));
}
}
}
}
int fa[M],val[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void kruscal()
{
tot=n,cnt=0;
memset(head,0,sizeof(head));
for(int i=1;i<=n*2;++i) fa[i]=i;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot;
fa[x]=fa[y]=tot,val[tot]=e[i].dis;
add(tot,x,0),add(x,tot,0),add(tot,y,0),add(y,tot,0);
if(tot==2*n-1) return ;
}
}
int f[M][20];
inline void dfs(int u,int fx)
{
f[u][0]=fx;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==fx) continue;
dfs(v,u);
dis[u]=min(dis[u],dis[v]);
}
}
inline int query(int v,int p)
{
for(int i=19;i>=0;--i)
{
if(f[v][i]&&val[f[v][i]]>p) v=f[v][i];//如果我有这个祖先，并且祖先的权值大于降水就可以跳
}
return dis[v]; //最后输出祖先预处理出来的值
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>T;
while(T--)
{
cnt=0,memset(head,0,sizeof(head));
cin>>n>>m;
for(int i=1,u,v,l,a;i<=m;++i)
{
cin>>u>>v>>l>>a;
add(u,v,l),add(v,u,l);
e[i]=(edge){u,v,a};
}
dijkstra(1),kruscal();//跑关于点 1 的单源最短路径+依海拔建重构树
dfs(tot,0);//预处理重构树中每个点手下的叶子节点到 1 的最短路径，同时找到每个点的父亲，为倍增跳父亲做准备
for(int j=1;j<=19;++j)
{
for(int i=1;i<=n*2;++i) f[i][j]=f[f[i][j-1]][j-1];
}//预处理倍增数组，注意点数此时是2n-1（直接写2n也没影响）
cin>>q>>k>>s;
int lastans=0;
for(int i=1,v0,p0;i<=q;++i)
{
cin>>v0>>p0;
v0=(v0+k*lastans-1)%n+1,p0=(p0+k*lastans)%(s+1);
lastans=query(v0,p0);//倍增跳
cout<<lastans<<"\n";
}
}
return 0;
}
CF1253F Cheap Robot
和上一道题比较像啊，但是充电中心有多个，相当于就是拥有多个起点，将这些点全部作为起点跑一边最短路，我们就知道每个点到最近的充电中心的距离了，记为 \(dis\)。（这个是最短路板子吧）。
那么还是设路径的权值为边权的最大值，现在要找一条权值最小的路径。但是按原边权建重构树可行吗，自然是不可行的，因为假设我们拥有值等于当前路径边权最大值的电池容量，但是我们没法保证每个点之间都是充电中心，每个点需要去离它最近的充电中心充电，那么现在对于一条 \(x \to y\) 权值为 \(w\) 的边，可以走这条边的前提当然是你的电池容量至少有 \(dis_x+w_dis_y\)，也就是从离 \(x\) 最近的充电中心赶过来，然后走过去，还能到达离 \(y\) 最近的充电中心。
于是跑完最短路之后，将各个边的边权修改一下，然后建最小生成树的 Kruskal 重构树，倍增/树剖求两点的LCA即可，这里用的是倍增。
代码：
const int M=3e5+5;
int n,m,k,q,idx;
int fax[M];
struct node{
int u,v,w;
inline bool operator < (const node &o) const
{
return w<o.w;
}
};node e[M];
vector<int> g[M];
int cnt=0;
struct N{
int to,next,val;
};N p[M<<1];
int head[M],dis[M],vis[M],c[M],val[M];//c数组没啥用
inline void add(int a,int b,int c)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
p[cnt].val=c;
}
inline int find(int x)
{
if(x!=fax[x]) fax[x]=find(fax[x]);
return fax[x];
}
inline void disj()
{
memset(dis,0x3f,sizeof(dis));
priority_queue<pair<int,int>> q;
for(int i=1;i<=k;++i) dis[i]=0,c[i]=i,q.push(make_pair(0,i));
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to,w=p[i].val;
if(dis[v]>dis[u]+w)
{
c[v]=c[u],dis[v]=dis[u]+w;
q.push(make_pair(-dis[v],v));
}
}
}
return ;
}//最短路
inline void merge(int x,int y)
{
g[x].push_back(y),fax[y]=x;
}
int deep[M],fa[M][23];
inline void dfs(int u,int f)
{
deep[u]=deep[f]+1,fa[u][0]=f;
for(int i=1;(1<<i)<=idx;++i) fa[u][i]=fa[fa[u][i-1]][i-1];
for(auto v:g[u]) if(v!=f) dfs(v,u);
}
inline int LCA(int x,int y)
{
if(deep[x]<deep[y]) swap(x,y);
int d=deep[x]-deep[y];
for(int i=0;(1<<i)<=d;++i) if((1<<i)&d) x=fa[x][i];
if(x==y) return x;
for(int i=22;i>=0;--i)
{
if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
}
return fa[x][0];
}//倍增跳LCA
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k>>q;
for(int i=1;i<=n*2;++i) fax[i]=i;
for(int i=1,a,b,c;i<=m;++i)
{
cin>>e[i].u>>e[i].v>>e[i].w;
add(e[i].u,e[i].v,e[i].w),add(e[i].v,e[i].u,e[i].w);
}
disj();
for(int i=1;i<=m;++i)
{
e[i].w+=dis[e[i].u]+dis[e[i].v];
}//更新新的边权
sort(e+1,e+m+1),idx=n;
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++idx;
merge(idx,x),merge(idx,y);
val[idx]=e[i].w;
}//建重构树
dfs(idx,0);
int x,y,res;
while(q--)
{
cin>>x>>y;
res=val[LCA(x,y)];
cout<<(res?res:-1)<<"\n";
}
return 0;
}
CF1416D Graph and Queries
大数据结构题，对于这种题还是先一步步分析。给定一个 \(n\) 个点 \(m\) 条边的无向图，第 \(i\) 个点的点权初始值为 \(p_i\),所有 \(p_i\) 互不相同，接下来进行 \(q\) 次操作，分为两类：
- \(\tt 1\ v\) 查询与 \(v\) 连通的点中， \(p_u\) 最大的点 \(u\) 并输出 \(p_u\)，然后让 \(p_u=0\)。
- \(\tt 2\ i\) 将第 \(i\) 条边删掉。
首先考虑维护操作 \(2\) ，发现除了 LCT 几乎已经没啥能维护断边了，而且全程只有断边没有加边，于是经典转化，正难则反，考虑将时间倒流，于是就变成了一步步加边。
然后再考虑操作 \(2\) ，和连通性相关啊，考虑 Kruskal 重构树的第四个性质就是与连通性相关，那么此时点权应该设为什么？自然是和时间相关，因为随着时间的推移，有一些边就断掉了，同时也就无法到达了。这非常的巧妙，点权是时间，那么边权也是时间，可以想到给每条边的边权就是其被删的时间，对于一直没被删的边，边权设为 \(q+1\) 即可。
于是加边的时候时间倒流也可以利用这个边权，将边权从大到小排序，然后一条一条插入回图中，同时建出 Kruskal 重构树，那么一个点权为 \(w\) 的点，其子树叶子节点，就是从这个点的子树某一点为起点，使用时间在 \(w\) 时还在的边，所能到达的所有点。给每个叶子节点都赋上一个 \(dfn\) 值， 每个点子树内叶子节点的 \(dfn\) 值就是连续的一段，dfs 一遍预处理出每个点子树内叶子节点的 \(dfn\) 区间。
于是我们对于查询区间最大值就可以使用线段树求解，将 \(p\) 值放在线段树上，对于当前询问的点 \(x\)，查看询问的时间，使其向上跳祖先刚好跳到祖先点的权值大于等于时间（当然这部分也需要使用倍增求解），然后这个祖先点子树内所有的叶子节点就是 \(x\) 可以遍历到的点，由于 \(dfn\) 值是连续的一段，所以依然可以用线段树查询。这题给我们简化了一下，由于各个点的 \(p\) 值都是不一样的，所以我们找到这个最大值之后我们就知道这个点是哪一个点了。（建立一个映射函数，虽然值域较大，需要离散化一下）当然还需要判断一下，如果权值为 \(0\) 就不管，否则把这个最大值对应的点的权值修改为 \(0\) 。（每个点的 \(dfn\) 值已知，直接线段树单点修改即可）。
代码：
const int M=6e5+5;
int n,m,q,tot;
int c[M],F[M],w[M];
int cnt=0;
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w>o.w;
}
};edge e[M];
struct ask{
int opt,x;
};ask s[M];
struct N{
int to,next;
};N p[M<<1];
int head[M],mapp[M];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int fa[M][20],lmax[M],rmax[M],num,id[M];
inline void dfs(int u,int f)
{
int flag=0;lmax[u]=inf;
fa[u][0]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
flag=1,dfs(v,u);
lmax[u]=min(lmax[u],lmax[v]),rmax[u]=max(rmax[u],rmax[v]);
}
if(!flag) lmax[u]=rmax[u]=++num,id[num]=u;
}
inline int find_pos(int x,int k)
{
for(int i=19;i>=0;--i)
{
if(w[fa[x][i]]>=k&&fa[x][i]) x=fa[x][i];
}
return x;
}
int tree[M<<2],res=0;
inline void build(int u,int ll,int rr)
{
if(ll==rr){tree[u]=c[id[ll]];return ;}
int mid=(ll+rr)>>1;
build(u<<1,ll,mid),build(u<<1|1,mid+1,rr);
tree[u]=max(tree[u<<1],tree[u<<1|1]);
}
inline void query(int u,int ll,int rr,int L,int R)
{
if(L<=ll&&rr<=R){res=max(res,tree[u]);return ;}
int mid=(ll+rr)>>1;
if(mid>=L) query(u<<1,ll,mid,L,R);
if(R>mid) query(u<<1|1,mid+1,rr,L,R);
}
inline void update(int u,int ll,int rr,int x)
{
if(ll==rr){tree[u]=0;return ;}
int mid=(ll+rr)>>1;
if(mid>=x) update(u<<1,ll,mid,x);
else update(u<<1|1,mid+1,rr,x);
tree[u]=max(tree[u<<1],tree[u<<1|1]);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>q,tot=n;
for(int i=1;i<=n*2;++i) F[i]=i;
for(int i=1;i<=n;++i) cin>>c[i],mapp[c[i]]=i;
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v,e[i].w=q+1;
for(int i=1;i<=q;++i)
{
cin>>s[i].opt>>s[i].x;
if(s[i].opt==2) e[s[i].x].w=i;
}//给每条边赋上权值
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot,add(tot,x),add(tot,y);
F[x]=F[y]=tot,w[tot]=e[i].w;
}//建重构树
for(int i=1;i<=tot;++i)
{
if(find(i)==i) dfs(i,0);//预处理出每个点子树内叶子节点dfn值的左右端
}//图可能不连通
for(int j=1;j<=19;++j)
{
for(int i=1;i<=tot;++i) fa[i][j]=fa[fa[i][j-1]][j-1];
}//处理出倍增数组
build(1,1,n);
for(int i=1,pos;i<=q;++i)
{
if(s[i].opt==2) continue;
pos=find_pos(s[i].x,i);//找到当前自己所能跳的最上面的祖先
res=0;
query(1,1,n,lmax[pos],rmax[pos]);//找最大值
if(res) update(1,1,n,lmax[mapp[res]]);//将最大值赋为0
cout<<res<<"\n";
}
return 0;
}
P4197 Peaks
也是神题了，数据结构码农题。
首先由于边有边权，点有点权，问你从起点 \(v\) 开始只经过困难度（边权）不超过 \(x\) 的边所能到达的山峰中第 \(k\) 高的边。
其实很板子，首先对于后面那句话，路径权值相当于就是路径上边的边权最大值，然后求一条路径权值不超过 \(x\) 所能到达的点，那么这不就是依据 Kruskal 重构树性质反过来说了一遍，于是选择建出重构树，某点下属的叶子节点就是从这个点内某一叶子节点出发，经过不超过点权的路径所能到达的点。
对于每组询问找到当前能跳到的最上面的祖先，于是这个祖先下属的叶子节点就是我们所能到达的所有山峰，由于山峰有高度（点权），让我们找出山峰中第 \(k\) 高峰，dfs 一遍树，对每个叶子节点赋上 \(dfn\) 值，每一个点下属的叶子节点的 \(dfn\) 值一定是一段。于是问题转化成了静态查询区间第 \(k\) 大值，套一个主席树板子。
代码：
const int M=5e5+5;
int n,m,q,tot,len;
int a[M],b[M],F[M],w[M];
int cnt=0;
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w<o.w;
}
};edge e[M];
struct N{
int to,next;
};N p[M];
int head[M];
inline void add(int a,int b)
{
//cout<<a<<" "<<b<<"\n";
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(F[x]!=x) F[x]=find(F[x]);
return F[x];
}
int dfn[M],num,id[M],lmax[M],rmax[M];
int fa[M][20];
inline void dfs(int u,int f)
{
int flag=0;lmax[u]=inf,fa[u][0]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
flag=1,dfs(v,u);
lmax[u]=min(lmax[u],lmax[v]),rmax[u]=max(rmax[u],rmax[v]);
}
if(!flag) lmax[u]=rmax[u]=++num,id[num]=u;
}
struct TREE{
int x,l,r;
};TREE tree[M<<5];
int root[M];
inline int build(int ll,int rr)
{
int u=++num;
tree[u].x=0;
if(ll<rr)
{
int mid=(ll+rr)>>1;
tree[u].l=build(ll,mid),tree[u].r=build(mid+1,rr);
}
return u;
}
inline int update(int pre,int ll,int rr,int x)
{
int u=++num;tree[u]=tree[pre];++tree[u].x;
if(ll<rr)
{
int mid=(ll+rr)>>1;
if(x<=mid) tree[u].l=update(tree[pre].l,ll,mid,x);
else tree[u].r=update(tree[pre].r,mid+1,rr,x);
}
return u;
}
inline int query(int u,int v,int ll,int rr,int k)
{
if(ll>=rr) return ll;
int mid=(ll+rr)>>1,x=tree[tree[v].l].x-tree[tree[u].l].x;
if(x>=k) return query(tree[u].l,tree[v].l,ll,mid,k);
else return query(tree[u].r,tree[v].r,mid+1,rr,k-x);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>q,tot=n;
for(int i=1;i<=(n<<1);++i) F[i]=i;
for(int i=1;i<=n;++i) cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1),len=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;++i) a[i]=lower_bound(b+1,b+len+1,a[i])-b;//权值很大，可能需要离散化一下
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot,add(tot,x),add(tot,y);
F[x]=F[y]=tot,w[tot]=e[i].w;
}//建重构树
for(int i=1;i<=tot;++i) if(find(i)==i) dfs(i,0);//可能不连通，给每个叶子赋dfn值
for(int j=1;j<=19;++j)
{
for(int i=1;i<=tot;++i) fa[i][j]=fa[fa[i][j-1]][j-1];
}//预处理倍增数组
num=0,root[0]=build(1,len);
for(int i=1;i<=n;++i)
{
root[i]=update(root[i-1],1,len,a[id[i]]);
}//将每个值插入主席树
int x,val,k,siz;
while(q--)
{
cin>>x>>val>>k;
for(int i=19;i>=0;--i)
{
if(fa[x][i]&&w[fa[x][i]]<=val) x=fa[x][i];
}//倍增跳祖先
siz=rmax[x]-lmax[x]+1;
if(siz<k) {cout<<"-1\n";continue;}
cout<<b[query(root[lmax[x]-1],root[rmax[x]],1,len,siz-k+1)]<<"\n";//主席树求区间第k大
}
return 0;
}
P7834 [ONTAK2010] Peaks 加强版
Kruskal 重构树是在线做法，可以过的。
AT_agc002_d [AGC002D] Stamp Rally
挺板的题，当时好像是贺的题解，现在感觉很简单啊。由于都告诉你问的是从两点 \(x,y\) 出发，至少到达 \(k\) 个点时，经过边的最大编号是多少。自然直接建出最小生成树 Kruskal 重构树。
然后分为两部分做，一部分是两个点跳祖先还没有跳到一个祖先上，还有一部分是两个跳祖先跳一起了，之后更上面的祖先当然也是一样的了。所以我们可以先查询一下 \(x,y\) 的 LCA，看 LCA 下属的点是否超过了 \(k\)。
没有超过就在权值为 \(1 \sim w_LCA\) 这个范围二分答案啊，对于当前 check 权值为 \(w\)，然后还是从两个点分别向上跳到刚好点权小于等于 \(w\) 的祖先，然后将找到的这两个祖先下辖的叶子节点之和是否大于等于 \(k\) ，这样时间复杂度是 \(O(n \cdot (\log_2 n)^2)\)（二分答案有一个 \(log\)，跳祖先倍增有一个 \(log\)）。超过了的话也是二分，只不过从 \(x,y\) 中任意一点跳就可以了，因为都是相同的，时间复杂度也是 \(O(n \cdot (\log_2 n)^2)\)，由于 \(n \leq 1e5\)，实现较优的话能过的（毕竟还给了 \(2s\) ）
代码（我是贺的，写法非常神仙）：
const int M=2e5+5;
int n,m,q;
int fa[M],fl[M],ed[M];
map<int,int> siz[M];
inline int find(int s,int lim=inf)//太震撼了，竟然是暴力跳的
{
while((fa[s]!=s)&&(fl[s]<=lim)) s=fa[s];
return s;
}
inline int check(int x,int y,int lim)
{
x=find(x,lim),y=find(y,lim);
if(x==y) return (--siz[x].upper_bound(lim))->second;
else return (--siz[x].upper_bound(lim))->second+(--siz[y].upper_bound(lim))->second;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) fa[i]=i,siz[i][0]=1;
for(int i=1,u,v;i<=m;i++)
{
cin>>u>>v;
u=find(u);v=find(v);
if(u==v) continue;
if(siz[u]>siz[v]) swap(u,v);
fa[u]=v,fl[u]=i,siz[v][i]=siz[v][ed[v]]+siz[u][ed[u]];
ed[v]=i;
}
cin>>q;
int x,y,lim;
while(q--)
{
cin>>x>>y>>lim;
int l=0,r=m;
while(l+1!=r)
{
int mid=(l+r)>>1;
if(check(x,y,mid)>=lim) r=mid;
else l=mid;
}
cout<<r<<"\n";
}
return 0;
}
CF1628E Groceries in Meteor Town
我觉得和上面几道题有共同之处吧，只给出代码（部分讲解放代码里了）。
代码：
const int M=6e5+5;
int n,q,tot;
int F[M],w[M];
int cnt=0;
struct edge{
int u,v,w;
inline bool operator <(const edge o) const
{
return w<o.w;
}
};edge e[M];
struct N{
int to,next;
};N p[M];
int head[M];
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
int lmax[M],rmax[M],num,id[M];
int fa[M][21],deep[M];
inline void dfs(int u,int f)
{
int flag=0;lmax[u]=inf,fa[u][0]=f,deep[u]=deep[f]+1;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
flag=1,dfs(v,u);
lmax[u]=min(lmax[u],lmax[v]),rmax[u]=max(rmax[u],rmax[v]);
}
if(!flag) lmax[u]=rmax[u]=++num,id[num]=u;
}
inline int lca(int x,int y)
{
if(deep[x]<deep[y]) swap(x,y);
for(int i=20;i>=0;--i)
{
if(deep[fa[x][i]]>=deep[y]) x=fa[x][i];
}
if(x==y) return x;
for(int i=20;i>=0;--i)
{
if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
}
return fa[x][0];
}
int lx,rx;
struct TREE{
int l,r,mx,mn,tag;
int rx,rn;bool vis;
};TREE tr[M*4];
#define ls u<<1
#define rs u<<1|1
inline void pushup(int u)
{
tr[u].vis=1;
if(!tr[ls].vis&&!tr[rs].vis)
{
tr[u].mx=max(tr[ls].mx,tr[rs].mx);
tr[u].mn=min(tr[ls].mn,tr[rs].mn);
tr[u].vis=0;
}
else if(!tr[ls].vis)
{
tr[u].mx=tr[ls].mx;
tr[u].mn=tr[ls].mn;
tr[u].vis=0;
}
else if(!tr[rs].vis)
{
tr[u].mx=tr[rs].mx;
tr[u].mn=tr[rs].mn;
tr[u].vis=0;
}
}
inline void pushdown(int u)
{
if(tr[u].tag==-1)return ;
if(tr[u].tag==1)
{
tr[ls].tag=tr[rs].tag=1;
tr[ls].vis=tr[rs].vis=1;
tr[ls].mx=tr[rs].mn=0;
tr[ls].mn=tr[rs].mn=inf;
tr[u].tag=-1;
}
if(tr[u].tag==0)
{
tr[ls].vis=tr[rs].vis=0;
tr[ls].tag=tr[rs].tag=0;
tr[ls].mx=tr[ls].rx;tr[ls].mn=tr[ls].rn;
tr[rs].mx=tr[rs].rx;tr[rs].mn=tr[rs].rn;
tr[u].tag=-1;
}
}
inline void build(int u,int l,int r)
{
tr[u].l=l;tr[u].r=r;
tr[u].vis=1;tr[u].tag=-1;tr[u].mn=inf;
if(l==r)
{
tr[u].rn=tr[u].rx=lmax[l];
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
tr[u].rx=max(tr[ls].rx,tr[rs].rx);
tr[u].rn=min(tr[ls].rn,tr[rs].rn);
}
inline void update(int u,int cl,int cr,int x)
{
if(tr[u].l>=cl&&tr[u].r<=cr)
{
tr[u].tag=x;
tr[u].vis=x;
if(x==1)
{
tr[u].mn=inf;
tr[u].mx=0;
}
if(x==0)
{
tr[u].mx=tr[u].rx;
tr[u].mn=tr[u].rn;
}
return ;
}
pushdown(u);
int mid=(tr[u].l+tr[u].r)>>1;
if(mid>=cl&&tr[ls].tag!=x)update(ls,cl,cr,x);
if(mid<cr&&tr[rs].tag!=x)update(rs,cl,cr,x);
pushup(u);
}
inline void query(int u,int cl,int cr)
{
if(u==1) lx=inf,rx=0;
if(tr[u].l>=cl&&tr[u].r<=cr)
{
if(!tr[u].vis)
{
lx=min(lx,tr[u].mn);
rx=max(rx,tr[u].mx);
}
return ;
}
pushdown(u);
int mid=(tr[u].l+tr[u].r)>>1;
if(mid>=cl)query(ls,cl,cr);
if(mid<cr)query(rs,cl,cr);
pushup(u);
}//线段树维护的是当前点的颜色，以及某段区间中白色点dfn的最小最大值
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q,tot=n;
for(int i=1;i<=(n<<1);++i) F[i]=i;
for(int i=1;i<n;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+n);
for(int i=1,x,y;i<n;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot,F[x]=F[y]=tot,w[tot]=e[i].w;
add(tot,x),add(tot,y);
}//建重构树
dfs(tot,0);
for(int j=1;j<=20;++j)
{
for(int i=1;i<=tot;++i) fa[i][j]=fa[fa[i][j-1]][j-1];
}//倍增数组
build(1,1,n);
int opt,l,r,x,flag;
while(q--)
{
cin>>opt;
if(opt==1) cin>>l>>r,update(1,l,r,0);//将一段全部赋0
else if(opt==2) cin>>l>>r,update(1,l,r,1);//全部赋1
else
{
cin>>x;
query(1,1,n);
if((lx==rx&&id[lx]==x)||rx==0) {cout<<"-1\n";continue;}
cout<<max(w[lca(x,id[lx])],w[lca(x,id[rx])])<<"\n";//找到dfn的最小最大值之后，x与所有白色点的LCA最上面的可能性就知道了，LCA越上面权值越大，找出x&dfn最小值对应的点的LCA权值与x&dfn最大值对应的点的LCA权值
}
}
return 0;
}
AT_joisc2014_e 水筒
这题是上面那道询问电池最小容量的弱化版吧。一样的做法。
代码：
const int M=4e6+5,N=2e3+5;
int h,w,p,q,cnt;
char s[N];
int f[M],dep[M];
int dx[5]={0,1,-1,0,0},dy[5]={0,0,0,1,-1};
int a[N][N],dis[N][N],fa[M][25],maxx[M][25];
struct node{
int x,y;
};queue<node>qq;
vector<node>e[M];
struct edge{
int x,y,dis;
}t[M];
inline bool cmp(edge x,edge y){return x.dis<y.dis;}
inline int find(int x)
{
if(f[x]!=x) return f[x]=find(f[x]);
return x;
}
inline void dfs(int x,int fat)
{
dep[x]=dep[fat]+1;
for(int i=0;i<e[x].size();++i)
{
int y=e[x][i].x,w=e[x][i].y;
if(y==fat) continue;
fa[y][0]=x,maxx[y][0]=w;
for(int j=1;j<=20;++j)
{
fa[y][j]=fa[fa[y][j-1]][j-1],maxx[y][j]=max(maxx[y][j-1],maxx[fa[y][j-1]][j-1]);
}
dfs(y,x);
}
}
inline int lca(int x,int y)
{
int ans=0;
if(dep[x]>dep[y]) swap(x,y);
for(int i=20;i>=0;i--)
{
if(dep[x]+(1<<i)<=dep[y]) ans=max(ans,maxx[y][i]),y=fa[y][i];
}
if(x==y) return ans;
for(int i=20;i>=0;i--)
{
if(fa[x][i]!=fa[y][i])
{
ans=max(ans,max(maxx[x][i],maxx[y][i])),x=fa[x][i],y=fa[y][i];
}
}
return max(ans,max(maxx[x][0],maxx[y][0]));
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>h>>w>>p>>q;
for(int i=1;i<=h;++i)
{
cin>>s;
for(int j=0;j<w;++j) if(s[j]=='#') a[i][j+1]=-1;
}//平面图转化一下
for(int i=1,x,y;i<=p;++i)
{
f[i]=i,cin>>x>>y,a[x][y]=i;
qq.push((node){x,y});
}
while(!qq.empty())
{
int x=qq.front().x,y=qq.front().y;
qq.pop();
for(int i=1;i<=4;++i)
{
int u=x+dx[i],v=y+dy[i];
if(u<1||u>h||v<1||v>w||a[u][v]==-1) continue;
if(a[u][v]==0)
{
a[u][v]=a[x][y];
dis[u][v]=dis[x][y]+1;
qq.push((node){u,v});
continue;
}
if(a[u][v]!=a[x][y]) t[++cnt]=((edge){a[u][v],a[x][y],dis[u][v]+dis[x][y]});
}
}
sort(t+1,t+cnt+1,cmp);
int tot=0;
for(int i=1;i<=cnt;++i)
{
int u=t[i].x,v=t[i].y,w=t[i].dis;
int x=find(u),y=find(v);
if(x!=y)
{
f[x]=y,++tot;
e[x].push_back((node){y,w});
e[y].push_back((node){x,w});
if(tot==cnt-1) break;
}
}
for(int i=1;i<=p;++i) if(!dep[i]) dfs(i,0);
for(int i=1,s,t;i<=q;++i)
{
cin>>s>>t;
if(find(s)!=find(t)) cout<<-1<<"\n";
else cout<<lca(s,t)<<"\n";
}
return 0;
}
还有一道写过代码的 Kruskal 重构树：
#LOJ 6493. graph
额，还是把他的讲解放到 dsu on tree 的博客吧，一道树上启发式合并+重构树+树状数组的好题。
代码：
const int M=8e5+5,limit=2e5;
int n,m,k,tot,maxson;
int a[M],F[M],w[M];
int cnt=0;
struct N{
int to,next;
};N p[M];
int head[M];
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w<o.w;
}
};edge e[M];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a],head[a]=cnt,p[cnt].to=b;
}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int fa[M],siz[M],deep[M],son[M];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int tree[M];
inline int lowbit(int x){return x&-x;}
inline void update(int x,int k)
{
while(x<=limit) tree[x]+=k,x+=lowbit(x);
}
inline int query(int x)
{
int sum=0;
while(x) sum+=tree[x],x-=lowbit(x);
return sum;
}
int res,ans;
inline void solve(int u,int f,int opt)
{
if(u<=n)
{
if(opt==1)
{
if(a[u]-k>=1) res+=query(a[u]-k);
if(a[u]+k<=limit) res+=query(limit)-query(a[u]+k-1);
}
else if(opt==2) update(a[u],1);
else update(a[u],-1);
}
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
solve(v,u,opt);
}
}
inline void dfs2(int u,int f,int opt)
{
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f||v==son[u]) continue;
dfs2(v,u,0);
}
if(son[u]) dfs2(son[u],u,1),maxson=son[u];
res=0;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==son[u]) continue;
solve(v,u,1);
//扫完一个子树,加上一个子树
solve(v,u,2);
}
ans+=res*w[u];
if(u<=n&&!opt) return ;
else if(u<=n&&opt) update(a[u],1);
else if(!opt) solve(u,f,3);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k,tot=n;
for(int i=1;i<=(n<<1);++i) F[i]=i;
for(int i=1;i<=n;++i) cin>>a[i],++a[i];
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++tot,add(tot,x),add(tot,y);
F[x]=F[y]=tot,w[tot]=e[i].w;
}
dfs1(tot,0,1);
dfs2(tot,0,1);
cout<<ans<<"\n";
return 0;
}
P3684 [CERC2016] 机棚障碍 Hangar Hurdles
md，这题恶心到我了，调了快一个小时。
首先对于一张平面，有一些障碍点，一个集装箱的坐标为其中心格子的坐标。集装箱可以向上下左右移动，但不能碰到障碍物，且不能移出仓库的边界，集装箱是一个 \(k*k\) 的矩形（\(k\) 为奇数），判断从一个位置移动到另一个位置可以移动的集装箱最大边长为多少。
那么首先先对每个点预处理一下障碍点/边界离他最近的曼哈顿距离（也就是这个点可能放置的最大的集装箱），可以记 # 的权值为 \(1\)，然后做一遍前缀和，对于每一个点，二分答案出它可能放置的最大的集装箱，判断就是判断这个矩阵内没有 # 且没有超过边界（使用二维前缀和快速判断）。
然后此时每个点的点权就是其可以放置的最大的集装箱（同时对于 # 所在的点点权记为 \(-1\)），然后网格图连边（连的下 ，\(2*n^2\)条 ）。那么边权是什么，自然就是这个边连接的两个点的点权较小值。对于一条路径权值条路径上的边的边权最小值，询问一条权值最大的路径。
于是套路的建最大生成树的 Kruskal 重构树，然后对于每个询问就查询两个点的 LCA 即可，若 LCA 点权为 -1，那么输出 \(0\)，其余情况就是 \(2*w_LCA+1\)。
代码：
const int M=1e3+5,N=2e6+5,inf=2e9;
int n,q,tot,idx;
int w[N],F[N],a[M][M];
bool vis[M][M];
int cnt=0;
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w>o.w;
}
};edge e[N];
struct Edge{
int to,next;
};Edge p[N];
int head[N];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int pos(int i,int j) {return (i-1)*n+j;}
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
int ax,ay,bx,by;
inline int check(int i,int j,int x)
{
ax=i-x,ay=j-x,bx=i+x,by=j+x;
if(ax<1||ay<1||bx>n||by>n||a[bx][by]-a[bx][ay-1]-a[ax-1][by]+a[ax-1][ay-1]!=0) return 0;//超边界了或矩阵内有#
return 1;
}
inline void init()
{
char opt;
for(int i=1;i<=2*n*n;++i) F[i]=i;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
cin>>opt,vis[i][j]=(opt=='#');
a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+vis[i][j];
}
}
for(int i=1,l,r,mid;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
if(vis[i][j]) {w[pos(i,j)]=-1;continue;}
l=0,r=n/2;
while(l<r)
{
mid=(l+r+1)>>1;
if(check(i,j,mid)) l=mid;
else r=mid-1;
}
w[pos(i,j)]=l;//二分预处理
}
}
}
int deep[N],fa[N],siz[N],son[N];
int id[N],num,top[N];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
inline void dfs2(int u,int topp)
{
id[u]=++num,top[u]=topp;
if(!son[u]) return ;
dfs2(son[u],topp);
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(!top[v]) dfs2(v,v);
}
}
inline int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(deep[x]>deep[y]) return y;
return x;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n,init();
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
if(i!=n) e[++tot]=(edge){pos(i,j),pos(i+1,j),min(w[pos(i,j)],w[pos(i+1,j)])};
if(j!=n) e[++tot]=(edge){pos(i,j),pos(i,j+1),min(w[pos(i,j)],w[pos(i,j+1)])};
}
}
sort(e+1,e+tot+1),idx=n*n;
for(int i=1,x,y;i<=tot;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
++idx,F[x]=F[y]=idx;
add(idx,x),add(idx,y);
w[idx]=e[i].w;
}//板子
dfs1(idx,0,1),dfs2(idx,idx);
cin>>q;int x;
while(q--)
{
cin>>ax>>ay>>bx>>by;
x=w[LCA(pos(ax,ay),pos(bx,by))];
if(x==-1) cout<<"0\n";
else cout<<x*2+1<<"\n";
}//板子+1
return 0;
}
后面的都做为练习题吧（毕竟都是口胡的，不给代码有点说不过去ing，看以后会不会补啊）。
