并查集+最小生成树 学习笔记+杂题 1
图论系列：
前言：
相关题单：戳我
算法讲解：戳我
代码可能过多啊，到时候页面别卡死了，所以就把代码最前面的缺省源删了（反正就是几个头文件/define int long long，自己加一下即可）。
并查集记得初始化，最小生成树记得排序。
P3367 【模板】并查集
板子题，给定 \(n\) 个元素，有 2 种操作，一种合并，一种询问是否在同一集合内。
唔唔，是算法讲解里并查集的初始化+路径压缩查询+合并操作，也是并查集的基础运用。
代码：
const int M=1e4+5;
int n,q;
int fa[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++) fa[i]=i;
int opt,x,y;
while(q--)
{
cin>>opt>>x>>y;
if(opt==1)
{
int a=find(x),b=find(y);
if(a==b) continue;
fa[a]=b;
}
else
{
int a=find(x),b=find(y);
if(a==b) cout<<"Y\n";
else cout<<"N\n";
}
}
return 0;
}
P3366 【模板】最小生成树
板子题。使用 Kruskal 求最小生成树。
按边权大小从小到大排序之后，使用并查集维护当前边连接的两点是否已经在同一个集合内了，如果在就跳过，不在就加入这条边，然后在并查集中将这两点合并起来。
注意图可能存在不连通的情况，所以每成功加入一条边就记录一下，根据树的性质：点数=边数+1，如果加入的边数等于 \(n-1\) 时，就可以输出答案了，此时加入的边已经让图联通了。否则最后输出 orz。
代码：
const int M=2e5+5;
int n,m,ans,num;
int fa[M];
struct edge{
int u,v,w;
inline bool operator <(const edge &o) const
{
return w<o.w;
}//结构体内置排序，实际上就是按边权从小到大排，手写cmp一样的
};edge e[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集
for(int i=1;i<=m;i++) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);//按边权排序
for(int i=1,x,y;i<=m;i++)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
ans+=e[i].w,fa[x]=y,++num;
if(num==n-1)//成功加入 n-1 条边
{
cout<<ans<<"\n";
return 0;
}
}
cout<<"orz\n";
return 0;
}
P3144 [USACO16OPEN] Closing the Farm S
经典trick，在很多包含删除操作的题会用到。给定一张无向图，\(n\) 个点 \(m\) 条边，给定删去点的顺序，每一个点被删的时同时删去与其相连的边。询问在给定顺序的第 \(i-1\) 个点被删去后，剩下的图是否是一张无向连通图（还在的点互相连通）。
并查集虽然可以判断当前存在的集合个数，但是没法处理这种删除的操作（并查集只能处理单点从某个集合移出的操作）。那么考虑正难则反，我们可以将删除的顺序颠倒过来，于是就变成了加边的操作，这时候并查集既可以处理了。
问题转化成，给定一些边，按照顺序加入一些点，观察现在的图是否连通，如何用并查集判断当前有多少个连通块？简单，首先加入一个点肯定就会多一个连通块，但是遍历与其相连的边，如果成功加入 \(x\) 条边，那么连通块就少了 \(x\) 个。
代码：
const int M=2e5+5;
int n,m,res;
int a[M],fa[M],ans[M],vis[M];
int cnt=0;
struct N{
int to,next;
};N p[M<<1];
int head[M];
inline void add(int a,int b)
{
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b;
}
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b),add(b,a);
for(int i=1;i<=n;++i) cin>>a[i],fa[i]=i;
for(int i=n,u,v,fx,fy;i>=1;--i)//反着来
{
u=a[i],res=0,vis[u]=1;//标记当前点已经在图中了
for(int j=head[u];j!=0;j=p[j].next)//遍历与这个点相连的边
{
v=p[j].to;
if(!vis[v]) continue;//如果通过这条边相连的点还没有出现在图中就不管
fx=find(u),fy=find(v);
if(fx!=fy) fa[fx]=fy,++res;//统计成功加入的边数
}
ans[i]=ans[i+1]-res+1;//当前连通块=上一次操作后的连通块-因为我新加的边而减少了res的连通块+一开始我是独立的
}
for(int i=1;i<=n;++i)
{
if(ans[i]==1) cout<<"YES\n";//如果只有一个连通块
else cout<<"NO\n";
}
return 0;
}
P2814 家谱
由于给定的是各个人的名字，所以拿一个 map 将每一个名字映射为一个数，因为最后输出的是名字，再用一个 map，将每个名字映射的数映射回去。查询祖先就是查询当前集合的根。
代码：
const int M=5e4+5;
string s;
int fa[M];
map<string,int> mapp;
map<int,string> str;//两个map负责 名字->数字 数字->名字
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int idx=0,a=0,b=0,q=0;char opt;
for(int i=1;i<M;i++) fa[i]=i;
while(1)
{
cin>>opt;
if(opt=='$') break;
cin>>s;
if(opt=='#')
{
if(!mapp[s]) mapp[s]=++idx,str[idx]=s;//出现了一个新名字
b=mapp[s];
}
else if(opt=='+')//+就是merge的操作，注意题目中给定操作描述说的谁是谁的祖先
{
if(!mapp[s]) mapp[s]=++idx,str[idx]=s;
a=mapp[s];
int x=find(a),y=find(b);
if(x==y) continue;
fa[x]=y;
}
else
{
q=mapp[s];
find(q);
cout<<s<<" "<<str[fa[q]]<<"\n";
}
}
return 0;
}
P1547 [USACO05MAR] Out of Hay S
按照最小生成树一个一个加进去，那么由于边权是按从小到大排序了的，所以最后一条加进去的边就是最小的。（woc，多久前写的了，竟然拿了个变量存加入的边的权值的最大值，有点多此一举了）
代码：
const int M=1e4+5;
int n,m,tot,maxx;
int fa[M];
struct N{
int u,v,w;
};N p[M];
inline bool cmp(N a,N b) {return a.w<b.w;}
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=1;i<=m;++i) cin>>p[i].u>>p[i].v>>p[i].w;
sort(p+1,p+m+1,cmp);
for(int i=1,fx,fy;i<=m;++i)
{
fx=find(p[i].u),fy=find(p[i].v);
if(fx==fy) continue;
fa[fx]=fy,++tot;
maxx=max(maxx,p[i].w);//喵
if(tot==n-1) break;
}
cout<<maxx<<"\n";
return 0;
}
P2330 [SCOI2005] 繁忙的都市
上一道题的多倍经验。
P1111 修复公路
上一道题的多倍经验。
P1551 亲戚
板子题，和板子只差了个输出。
P3535 [POI2012] TOU-Tour de Byteotia
贪心题，但是证明可能会有点绕（oi是这样的）。一张无向图上，\(n\) 个点 \(m\) 条边，询问至少需要删除几条边才能使得前 \(k\) 个点不在环上，题面要求输出删除的边，但是数据没要求（现在不知道力）。
首先对于一条边 \(u \to v\)，如果 \(u>k\) 且 \(v>k\) 的话它是影响不到前 \(k\) 个点的，所以这些边一定不被删，并使用并查集将这些边全部加进去。再枚举其他的边，如果边 \(u \to v\)，两点 \(u,v\) 的祖先相同，那么现在已经加入的边就已经使得这两个点连通了，再加上这条边就必成环，所以这条边就需要删，否则这条边不被删，加入并查集中。
代码：
const int M=1e6+5;
int n,m,k,ans;
int u[M],v[M],fa[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k;
ans=m;
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
cin>>u[i]>>v[i];
if(u[i]>k&&v[i]>k)
{
int x=find(u[i]),y=find(v[i]);
ans--;//这种边不会被删
if(x==y) continue;
fa[x]=y;
}
}
for(int i=1;i<=m;i++)
{
if(!(u[i]>k&&v[i]>k))
{
int x=find(u[i]),y=find(v[i]);
if(x==y) continue;
fa[x]=y,ans--;//这种加入进去两边不成环的也不会被删
}
}
cout<<ans<<"\n";
return 0;
}
P1955 [NOI2015] 程序自动分析
给定 \(k\) 个约束关系形如 \(i,j,e\)，若 \(e=1\) 表示 \(x_i=x_j\)，否则表示 \(x_i \neq x_j\)，询问各个约束条件是否存在矛盾。
有等于和不等于的关系，那么我们可以考虑等于就相当于并查集中的合并操作，不等于就相当于并查集中的祖先不一样。那么我们先将所有等于的操作处理完，将满足等于的各个变量合并在一起，然后对于每个不等的约束判断 \(i,j\) 的祖先相不相同，如果不相同就出现了矛盾。
注意：本题的 \(i,j\) 相当大，需要离散化（这是一个很常用的操作，是对于只关注数的相对大小而不在意数的绝对大小时，数的绝对大小较大，想将数约束在较小范围的操作），主要有两种做法，一种是二分，还有一种是 map，进行映射（建议参考网上资料）。
代码（有点古老了）：
const int M=200005;
int T,n;
int a[M],b[M],c[M],fa[M],l[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
cin>>T;
while(T--)
{
int tot=0;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i]>>b[i]>>c[i];
l[++tot]=a[i],l[++tot]=b[i];
}
sort(l+1,l+tot+1);
int len=unique(l+1,l+tot+1)-l-1;
int maxx=0;
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(l+1,l+len+1,a[i])-l;
b[i]=lower_bound(l+1,l+len+1,b[i])-l;//二分离散化的方法
maxx=max(maxx,max(a[i],b[i]));
}
for(int i=1;i<=maxx;i++) fa[i]=i;
for(int i=1;i<=n;i++)
{
if(c[i])//将所有相等的操作合并
{
int x=find(a[i]),y=find(b[i]);
if(x!=y) fa[x]=y;
}
}
int flag=0;
for(int i=1;i<=n;i++)
{
if(!c[i])//将所有不等的操作进行判断
{
int x=find(a[i]),y=find(b[i]);
if(x==y)
{
flag=1;
break;
}
}
}
if(flag) cout<<"NO\n";
else cout<<"YES\n";
}
return 0;
}
P1892 [BOI2003] 团伙
拓展域并查集的板子题（严格上来说拓展域能做的带权并查集都可以做，这里先介绍拓展域并查集）。
拓展域并查集主要适用范围是对于点与点之间可能存在多种状态（一般较小，多数时候为 2），例如这题就存在两种状态：朋友与敌人。
那么这时候对于每一个点还是朴素的进行并查集就有点力不从心了，所以对于这道题，我们可以对于一个点建一个反点，于是对于每个人就有两个点： \(i\) 表示正点，与 \(i\) 的朋友们相连，\(i+n\) 表示反点，与 \(i\) 的敌人们相连，当然初始化都是初始化的 \(fa_i=i\) 。这个时候题目中的两个操作就简单了：
对于是朋友的两个人：将 \(x\) 与 \(y\) 合并（为何不合并 \(x+n\) 与 \(y+n\)，因为题目中没有说敌人的朋友是敌人，那就不管了）。
对于是敌人的两个人：将 \(x\) 与 \(y+n\) 合并，将 \(x+n\) 与 \(y\) 合并。
其实发现，\(i+1 \sim 2n\) 充当了一个中转点的角色，负责将自己的敌人与自己的另外一堆敌人相连（至于点与点还存在更多种状态，也是形如这样做）。
最后询问最多的团体数，那就是 \(fa_i=i\) 的节点数，当然只统计 \(1 \sim n\) 的点。
代码：
const int M=1e4+5;
int n,q,ans;
int fa[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<=(n<<1);i++) fa[i]=i;//初始化2*n个点，空间也要开2倍
char opt;int x,y;
while(q--)
{
cin>>opt>>x>>y;
if(opt=='F') fa[find(x)]=find(y);
else
{
fa[find(x+n)]=find(y);
fa[find(y+n)]=find(x);
}
}
for(int i=1;i<=n;i++)
{
if(find(i)==i) ++ans;
}
cout<<ans<<"\n";
return 0;
}
P1525 [NOIP2010 提高组] 关押罪犯
和上一道题很像，但是转化的过程难想多了。由于现在我们有 2 个监狱，我们没法具体的操控某个人前往哪个监狱，但是我们可以判断两个人是否在同一个监狱啊！
所以某两个点之间就存在两种情况：在同一个监狱和不在同一个监狱。考虑逻辑 \(a\) 与 \(b\) 在同一个监狱，\(b\) 和 \(c\) 在同一个监狱，那么 \(a\) 与 \(c\) 在同一个监狱；\(a\) 与 \(b\) 不在同一个监狱，\(a\) 与 \(c\) 不在同一个监狱，那么 \(b\) 和 \(c\) 就一定在同一个监狱了，这下就和上一题的操作一样了，还是采用拓展域并查集进行求解。
但本题中是想让爆发冲突的影响力最小，那么对于影响力大的两人肯定选择先行放到两个不同的监狱，直到对于其中一组会爆发冲突的两人已经被放在同一个监狱了，那么这时候爆发的影响力一定就是最小的。（因为两人都为了避免爆发影响力更大的事件而不得不被分配到了这一个监狱）。
对于还没有到不得不在在一起的两人 \(x,y\)，在并查集里加入这两人不在一个监狱的指令，合并 \(x,y+n\) 与 \(x+n,y\)。
代码：
const int M=1e5+5;
int n,m;
int fa[M];
struct N{
int a,b,x;
};N p[M];
inline bool cmp(N a,N b)
{
return a.x>b.x;
}//按影响力从大到小排序
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void merge(int a,int b)
{
int x=find(a),y=find(b);
fa[x]=y;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++) cin>>p[i].a>>p[i].b>>p[i].x;
for(int i=1;i<=2*n;i++) fa[i]=i;//初始化2倍
sort(p+1,p+m+1,cmp);
for(int i=1;i<=m;i++)
{
int x=find(p[i].a),y=find(p[i].b);
if(x==y)//如果此时两人已经在同一个监狱了
{
cout<<p[i].x<<"\n";
return 0;
}
merge(p[i].a+n,p[i].b),merge(p[i].b+n,p[i].a);//否则这两个人不在同一个监狱
}
cout<<"0\n";
return 0;
}
P8710 [蓝桥杯 2020 省 AB1] 网络分析
\(n\) 个节点，\(m\) 个操作，共有两种操作：一种操作是表示将节点 \(a\) 和节点 \(b\) 通过连接起来，还有一种表示在节点 \(p\) 上发送一条大小为 \(t\) 的信息，此时所有与 \(p\) 相连的点都会收到这条信息，询问最后每个点接收到的信息大小总量。
考虑朴素的做法，对于操作 1 直接使用并查集合并即可，对于操作 2 ，暴力遍历一遍每个点，将所有与 \(p\) 祖先相同的点（同一集合）的权值加上 \(t\) 。
这样做时间复杂度肯定会爆，考虑优化，我们可以将权值 \(t\) 加在 \(p\) 的根上面，但是存在合并操作，每个点的根在变化。那么我们就在变化的时候——合并操作的时候将每个根节点上记录的权值下传即可，这样时间复杂度是 \(O(n^2)\) 级别的，因为最多只会合并 \(n\) 次。
代码：
const int M=1e5+5;
int n,q;
int fa[M],res[M],ans[M],siz[M];//ans记录的是第i个点的权值，res记录的是做为根当前还没有下传的权值
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;++i) fa[i]=i,siz[i]=1;
int opt,x,y,fx,fy;
while(q--)
{
cin>>opt>>x>>y;
if(opt==1)
{
fx=find(x),fy=find(y);
if(fx==fy) continue;
for(int i=1;i<=n;i++) ans[i]+=res[find(i)];//每次合并就把res下传下去
for(int i=1;i<=n;i++) res[i]=0;//清空res
if(siz[fx]>siz[fy]) swap(fx,fy);
fa[fx]=fy,siz[fy]+=siz[fx];
}
else res[find(x)]+=y;//x的根+y的待下传权值
}
for(int i=1;i<=n;++i) cout<<ans[i]+res[find(i)]<<" ";//最后答案是根节点上没有下传的权值+本点的权值
return 0;
}
P5836 [USACO19DEC] Milk Visits S
有点巧妙啊，这题做法其实挺多的，这里就介绍并查集的做法了。对于一条边相连的两个点，如果两端连接的颜色相同，那么就把它们合并。
那么判断的时候怎么判断？如果对于给定的图是一棵树，如果给定的路径 \(u \to v\) 上的点奶牛种类全部相同的话，那么 \(u,v\) 一定在同一个集合内，这个时候判断这个点代表的奶牛是否为客人喜欢的。那么如果这两点不在同一个集合内，就说明路径上有多种奶牛，那么一定能满足客人的需求，
代码：
const int M=1e5+5;
int n,m;
int fa[M];
char s[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>s[i],fa[i]=i;
int a,b,x,y;char opt;
for(int i=1,a,b,x,y;i<n;i++)
{
cin>>a>>b;
if(s[a]==s[b])//如果两点相同就合并
{
x=find(a),y=find(b);
fa[x]=y;
}
}
for(int i=1;i<=n;i++) find(i);
for(int i=1;i<=m;i++)
{
cin>>a>>b>>opt;
if(fa[a]==fa[b]&&s[fa[a]]!=opt) cout<<"0";//如果路径两端是在一个集合内（路径上全是一种奶牛&不和客人口味）
else cout<<"1";
}
return 0;
}
P5937 [CEOI1999] Parity Game
转化一下就是拓展域并查集，考虑对于每一个点 \(i\) 设其表示的是前 \(i\) 个数总共有奇数个 1 还是偶数个 1。
那么对于它的操作就比较显然了（先不考虑与前面是否矛盾），如果给定的区间 \(x \sim y\) 存在偶数个 1，那么 \(x\) 与 \(y\) 的奇偶性相同，反之存在奇数个 1 ，那么 \(x\) 与 \(y\) 的奇偶性不同。
于是用 \(i\) 表示与 \(i\) 奇偶性相同的点，\(i+n\) 表示与 \(i\) 奇偶性不同的点。但是这题和上面的板子题有一点不一样的是，与 \(z\) 奇偶性不相同的点 \(x\)，与 \(x\) 奇偶性相同的点 \(y\) ，\(z\) 一定也与 \(y\) 奇偶性不同（相当于给定了敌人的朋友也是敌人），所以在给定 \(x\) 与 \(y\) 奇偶性相同的条件时，还需要连接 \(x+n\) 与 \(y+n\) （成为朋友了之后一起对付彼此的敌人）。
那么判断矛盾也比较简单，如果 \(x\) 和 \(y\) 奇偶性相同，结果 \(x\) 和 \(y+n\) 在一起或者 \(y+n\) 与 \(x\) 在一起，另一种操作同理。
给定的下标大小过大，需要使用离散化处理（毕竟这题不在意序列下标的绝对大小）。
代码：
const int M=1e5+5;
int n,m,cnt=0;
int fa[M],c[M];
struct N{
int a,b,opt;
};N p[M];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void merge(int a,int b)
{
int x=find(a),y=find(b);
fa[x]=y;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;char opt[5];
for(int i=1;i<=m;i++)
{
cin>>p[i].a>>p[i].b>>opt;
p[i].a--;
if(opt[0]=='e') p[i].opt=0;
else p[i].opt=1;
c[++cnt]=p[i].a,c[++cnt]=p[i].b;
}
sort(c+1,c+cnt+1);
int len=unique(c+1,c+cnt+1)-c-1;
for(int i=1;i<=m;i++)
{
p[i].a=lower_bound(c+1,c+len+1,p[i].a)-c;
p[i].b=lower_bound(c+1,c+len+1,p[i].b)-c;
}//以上是离散化
for(int i=1;i<=2*m;i++) fa[i]=i;//预处理
for(int i=1;i<=m;i++)
{
if(!p[i].opt)//偶数个 奇偶相同
{
if(find(p[i].a)==find(p[i].b+m))
{
cout<<i-1<<"\n";return 0;
}
merge(p[i].a,p[i].b),merge(p[i].a+m,p[i].b+m);//a&b a+n&b+n
}
else//奇数个 奇偶相反
{
if(find(p[i].a)==find(p[i].b))
{
cout<<i-1<<"\n";return 0;
}
merge(p[i].a+m,p[i].b),merge(p[i].b+m,p[i].a);//a+n&b a&b+n
}
}
cout<<m<<"\n";
return 0;
}
P6121 [USACO16OPEN] Closing the Farm G
第三题的加强版，但是并查集都过得去，双倍经验了
P1197 [JSOI2008] 星球大战
上一题的多倍经验，只是点从 0 开始，输出的时候要求输出连通块的数量。
P1196 [NOI2002] 银河英雄传说
带权并查集的板子题，一开始有 30000 列，每列有一个战舰，现在有 2 种操作：
-
M i j：将 \(i\) 战舰所在的列拼到 \(j\) 战舰所在列的后面。 -
C i j：询问 \(i\) 与 \(j\) 号战舰是否在同一列，如果在同一列输出它们之间还有多少个战舰，否则输出 '-1' 。
考虑对于普通的并查集我们显然可以维护第一种操作和判断战舰是否在同一列。但是这里多了一种操作：询问两个战舰之间还有多少个战舰，这里显然普通的并查集没法解决。但是我们可以思考可以从朴素的并查集得到什么消息？显然我们可以得知每个点当前的根节点，那么我们可以对于每一个战舰维护其到根节点战舰的距离，由于战舰在同一列中是从前到后一个一个排的，对于两个点 \(x,y\)，设其到根节点的距离分别是 \(dis_x,dis_y\)，那么其中间的战舰数就是 \(abs(dis_x-dis_y)-1\) 了。
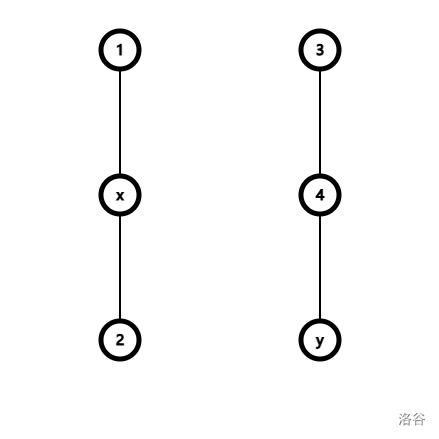
但是 \(dis\) 数组应该怎么维护，首先初始化的时候 \(dis_i=0\)，毕竟一开始每个点都是以自己为根的。要求是每一列的战舰从前到后一个一个排成一列（明显是没有路径压缩嘛），那我们也先不路径压缩，考虑最朴素的合并（如图），将两个点 \(x\) 与 \(y\) 所在的两列接在一起，\(x\) 所在集合放在 \(y\) 所在集合后面，那么一开始 \(dis_1=0,dis_x=1,dis_2=2,dis_3=0,dis_4=1,dis_y=2\)，合并之后变成了 \(dis_3=0,dis_4=1,dis_y=2,dis_1=3,dis_x=4,dis_2=5\)，发现 \(x\) 所在集合的每一个点的 \(dis\) 值加上了 \(y\) 所在集合的大小，所以对于每一个集合还需要维护集合的大小 \(siz\)，初始化 \(siz_i=1\) 。
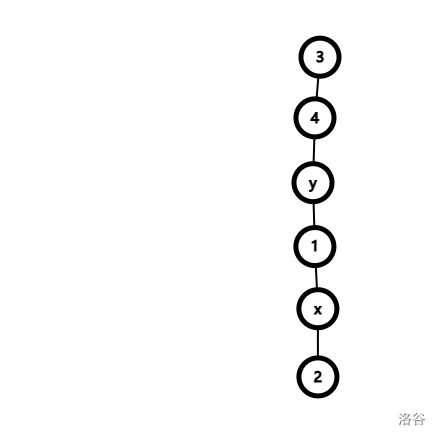
看样子差不多已经做完了，但是这是没有路径压缩的情况下，如果带权并查集也想要路径压缩应该怎么做？此时 \(dis_1=0,dis_x=1,dis_2=2,dis_3=0,dis_4=1,dis_y=2\)，我们已知路径压缩的时候肯定会经过自己头上的点，如点 \(x\) 想要路径压缩肯定会经过点 \(1\)。由于 \(x\) 集合内的每一个点 \(dis\) 值都加上了 \(siz_y\)，那么我们可以将这个值先存在点 1 的头上，下面的点路径压缩的时候一定会经过点 1，于是这个权值就加上了。
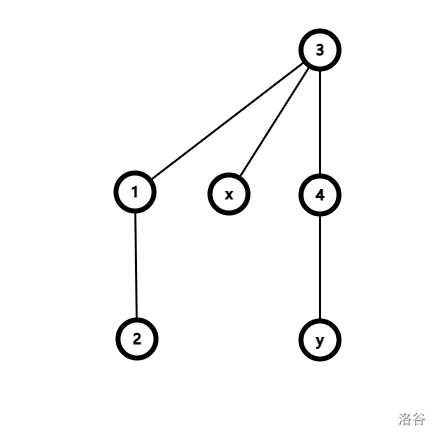
如图（当然了，这个图要是用了路径压缩应该不可能成这个样子，我们假设之前用的都是朴素的合并），我们现在直接像普通并查集那样将 \(1\) 直接连在 \(3\) 的下面，并赋 \(dis_1=3\)，然后查询点 \(x\) 的时候路径压缩。由于 \(dis_x=1,dis_1=3\)，\(x\) 向上跳的时候就加上其经过的点的权值，于是 \(dis_x=4\)，直接连向点 3，完成了路径压缩。
可以这么看，每一个点当前的权值实际上是到它原老板的距离，但是原老板现在又认了一个老板，原老板和现老板有一个距离，于是自己到现老板的距离就是自己到原老板的距离+原老板和现老板的距离，原老板和现老板的距离在向上跳的时候全部都被加上了，于是自己就可以成为现老板的直接下属了。
（讲的不是很好啊，qwq，看不懂再去搜搜其他的博客吧）。
代码：
const int M=3e4+5;
int q;
int fa[M],dis[M],siz[M];
inline int find(int x)
{
if(x==fa[x]) return fa[x];
else
{
int fax=fa[x];
fa[x]=find(fa[x]);
dis[x]+=dis[fax];
return fa[x];//加上各个老板之间的距离
}
}
inline int query(int a,int b)
{
int x=find(a),y=find(b);
if(x!=y) return -1;
return max(0,abs(dis[a]-dis[b])-1);
}
inline void merge(int a,int b)
{
int x=find(a),y=find(b);
if(x==y) return ;
fa[x]=y;//当前x直接挂在y后面
dis[x]=siz[y];//但是y这列现在已经有siz[y]个战舰了，于是x就是这列的siz[y]+1个战舰，到y的距离是siz[y]
siz[y]+=siz[x];//维护siz数组
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>q;
char opt;int a,b;
for(int i=1;i<M;i++) dis[i]=0,siz[i]=1,fa[i]=i;
while(q--)
{
cin>>opt>>a>>b;
if(opt=='M') merge(a,b);
else
{
cout<<query(a,b)<<"\n";
}
}
return 0;
}
P2024 [NOI2001] 食物链
由于有三类点，共有三种关系，不是很多，可以使用扩展域并查集。
对于一个点 \(i\)，点 \(i\) 相连的都是和自己一类的，\(i+n\) 相连的就是自己吃的，\(i+2*n\) 相连的是吃自己的。
那么对于操作一，对于两个点 \(x,y\) 是同类，如果 \(x,y\) 根据之前的条件不存在吃与被吃的关系，那么这句话就是真的，真的就将 \(x,y\)，\(x+n,y+n\)，\(x+2n,y+2n\) 相连，因为是一个种类了，两个点的猎物和天敌肯定就是共享的了。
对于操作二，对于两个点 \(x,y\)，存在 \(x\) 吃 \(y\) 的关系，只要不是有 \(y\) 吃 \(x\) 的关系或 \(x,y\) 是同一类，那么这句话是真的，是真的那么就把 \(x+n,b\) 相连，因为 \(i+n\) 连的是自己吃的。然后还要连接 \(x+2n,y+n\)，因为环形关系，自己吃另一类，那么另一类吃的一定就是吃自己的，再连接 \(x,y+2*n\)，因为 \(y\) 的天敌就是 \(x\) 了嘛。
连边要连完，还有自己是不吃自己的。
代码：
const int M=2e5+5;
int n,q,ans;
int fa[M];//一倍是自己，两倍是食物，三倍是天敌
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void merge(int a,int b)
{
int x=find(a),y=find(b);
fa[x]=y;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<=3*n;i++) fa[i]=i;
int opt,a,b;
for(int i=1;i<=q;i++)
{
cin>>opt>>a>>b;
if(a>n||b>n)
{
ans++;continue;
}
if(a==b&&opt==2)//自己不吃自己
{
ans++;continue;
}
if(opt==1)//两个是同类，所以不存在吃与被吃的关系
{
if(find(a)==find(b+n)||find(b)==find(a+n))
{
ans++;continue;
}
merge(a,b),merge(a+n,b+n),merge(a+2*n,b+2*n);
}
else
{
if(find(a)==find(b+n)||find(a)==find(b))//发现x吃y，所以xy不是同类&y不吃x
{
ans++;continue;
}
merge(a+n,b);//a吃的就是b
merge(a+2*n,b+n);//吃a的就是被b吃的，环形关系
merge(a,b+2*n);//b的天敌是a
}
}
cout<<ans<<"\n";
return 0;
}
P9869 [NOIP2023] 三值逻辑
扩展域并查集，就当练习题了（为啥我去年做不来啊┭┮﹏┭┮）。
P8074 [COCI2009-2010#7] SVEMIR
最小生成树的好题，考察一定的性质，观察题目，每个点有三个坐标 \((x_i,y_i,z_i)\)，在两点 \(A,B\) 之间连边的代价是 \(\min\{|x_A-x_B|,|y_A-y_B|,|z_A-z_B|\}\) 。考虑贪心，由于代价是每一维坐标差值的最小值，那么我们按照 \(x\) 排序，将相邻的两个星球连边一定能保证 \(|x_A-x_B|\) 最小，同理，按照 \(y\) 与 \(z\) 排序之后，跑一遍最小生成树即可。
代码：
int n;
int fa[100010];
long long ans=0;
int min(int x,int y) {return x>y?y:x;}
struct N{
int x,y,z,id;
};N a[100010];
int cnt=0;
struct M{
int u,v,w;
};M p[1000010];
bool cmpx(N a,N b){return a.x<b.x;}
bool cmpy(N a,N b){return a.y<b.y;}
bool cmpz(N a,N b){return a.z<b.z;}
bool cmp(M a,M b){return a.w<b.w;}
int find(int x)
{
if(x!=fa[x])
{
fa[x]=find(fa[x]);
}
return fa[x];
}
void kls()
{
sort(p+1,p+1+cnt,cmp);
int sum=0;
for(int i=1;i<=cnt;i++)
{
int fx=find(p[i].u),fy=find(p[i].v);
if(fx==fy) continue;
sum++;
ans+=p[i].w;
fa[fx]=fy;
if(sum+1==n) return ;
}
return ;
}
signed main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
a[i].id=i,fa[i]=i;
}
sort(a+1,a+n+1,cmpx);
for(int i=1;i<n;i++)
{
++cnt;
p[cnt].u=a[i].id,p[cnt].v=a[i+1].id;
p[cnt].w=min(abs(a[i].x-a[i+1].x),min(abs(a[i].y-a[i+1].y),abs(a[i].z-a[i+1].z)));
}
sort(a+1,a+n+1,cmpy);
for(int i=1;i<n;i++)
{
++cnt;
p[cnt].u=a[i].id,p[cnt].v=a[i+1].id;
p[cnt].w=min(abs(a[i].x-a[i+1].x),min(abs(a[i].y-a[i+1].y),abs(a[i].z-a[i+1].z)));
}
sort(a+1,a+n+1,cmpz);
for(int i=1;i<n;i++)
{
++cnt;
p[cnt].u=a[i].id,p[cnt].v=a[i+1].id;
p[cnt].w=min(abs(a[i].x-a[i+1].x),min(abs(a[i].y-a[i+1].y),abs(a[i].z-a[i+1].z)));
}
kls();
cout<<ans<<endl;
return 0;
}
P4255 公主の#18文明游戏
非常好的一道题，同时也是并查集启发式合并的板子题。
首先对于断边的操作，并查集几乎没法维护，所以考虑经典的转化，正难则反，将时间轴颠倒，变成一条一条向图中加边。那么有一个问题，由于一个城市中可能会有多个信仰的人，而且还需要将它们全部合并起来（应对询问对于 \(x\) 出发能到达的点选择 \(n\) 个人他们的信仰全是 \(c\) 的概率）。
由于路径压缩并查集只能知晓自己的根，那么肯定每一个在根下的城市将自己城市内所有的信仰者全部统计到根才能查询。观察到信仰的值域很大啊，你可以离线下来然后离散化一下，也可以用 map 直接做，对于每一个点 \(i\)，\(mapp_{i,j}\) 就是这个点信仰 \(j\) 的人数。
那么合并的时候也比较简单，对于两个根 \(x,y\)，将其合并为一个集合，那么只需要将 \(mapp_{x,i}\) 加到 \(mapp_{y,i}\) 中就可以了。此时就会出现一个问题，如果 \(x\) 中有很多种信仰，而 \(y\) 中只有一种信仰，那么每次合并的时候时间复杂度会爆。所以我们每次合并的时候考虑将信仰种类少的根加到信仰种类多的根（实际上就是 \(mapp[i].size()\)），这就是并查集的启发式合并（有点蠢啊，但跑起来真的快）。
至于最后概率的计算这个后面可能会讲，但不是这里的重点ing。
注：'map' 是一种非常方便的 STL，不会可以搜一下，能节省很多代码完成很多操作。
代码：
const int M=4e5+5,mod=19260817;
int n,m,k;
int fa[M],siz[M],num[M],f[M*10],ans[M];//num是总人数，计算概率时会用
map<int,int> mapp[M];
struct query{
int opt,x,y,z;
};query q[M];
struct node{
int x,y,vis;
};node p[M];
inline int quick(int a,int n)
{
int res=1;
while(n)
{
if(n&1) res=1ll*res*a%mod;
n>>=1,a=1ll*a*a%mod;
}
return res%mod;
}
inline int inv(int x){return quick(x,mod-2);}
inline int C(int n,int m){return 1ll*f[m]*inv(f[n])%mod*inv(f[m-n])%mod;}
//m里面选择n个
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void merge(int x,int y)
{
int fx=find(x),fy=find(y);
if(fx==fy) return ;
if(siz[fx]>siz[fy]) swap(fx,fy);
num[fy]+=num[fx],fa[fx]=fy;
for(auto it:mapp[fx]) mapp[fy][it.first]+=it.second;//map强大，此时相当于就是将fx中每个信仰的人数加到fy中了
siz[fy]=mapp[fy].size();
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k;
f[0]=1;
for(int i=1;i<=4e6;++i) f[i]=1ll*f[i-1]*i%mod;
for(int i=1;i<=n;++i) siz[i]=1,fa[i]=i;
for(int i=1,x,y;i<=n;++i) cin>>x>>y,mapp[i][y]+=x,num[i]=x;//初始化每个城市内的信仰
for(int i=1;i<=m;++i) cin>>p[i].x>>p[i].y;
for(int i=1;i<=k;++i)
{
cin>>q[i].opt;
if(q[i].opt==1)
{
cin>>q[i].x>>q[i].y>>q[i].z;
mapp[q[i].x][q[i].z]+=q[i].y;
siz[q[i].x]=mapp[q[i].x].size(),num[q[i].x]+=q[i].y;//离线下来，由于最后的时候都增加完了，所以现在需要将增加的操作都做了
}
else if(q[i].opt==2) cin>>q[i].x,p[q[i].x].vis=1;
else cin>>q[i].x>>q[i].y>>q[i].z;
}
for(int i=1;i<=m;++i) if(!p[i].vis) merge(p[i].x,p[i].y);
for(int i=k,tot,res;i>=1;--i)
{
if(q[i].opt==1) mapp[find(q[i].x)][q[i].z]-=q[i].y,num[find(q[i].x)]-=q[i].y;//由于时间倒流，原本加的操作现在变成减
else if(q[i].opt==2) merge(p[q[i].x].x,p[q[i].x].y);//删边也变成加边
else
{
tot=num[find(q[i].x)],res=mapp[find(q[i].x)][q[i].z];
if(res<q[i].y) {ans[i]=0;continue;}
//现在是要求选择q[i].y个捏
ans[i]=1ll*C(q[i].y,res)*inv(C(q[i].y,tot))%mod;//计算概率
}
}
for(int i=1;i<=k;++i)
{
if(q[i].opt==3) cout<<ans[i]<<"\n";
}
return 0;
}
P4185 [USACO18JAN] MooTube G
由于任意一对视频的相关性定义为沿此路径的任何连接的最小相关性。那么对于一个给定的 \(k\) 值，我们只能加入边权大于等于 \(k\) 的边。但是题目并不要求强制在线，我们可以将询问按 \(k\) 的值降序排序后离线解决本题。
由于 \(k\) 值降序，将边按边权从大到小排序之后，每次将当前询问允许的边添加进图中，每条边就只会被添加一次。那么对于询问的 点 \(x\)，其被推荐的点就是当前图中 \(x\) 所在的连通块大小 -1（因为不包含自己）。
代码：
const int M=1e5+5;
int n,q;
int fa[M],siz[M],ans[M];
struct N{
int u,v,w;
};N p[M];
struct P{
int id,x,w;
};P a[M];
inline bool cmp1(N a,N b)
{
return a.w>b.w;
}
inline bool cmp2(P a,P b)
{
return a.w>b.w;
}
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<n;i++) cin>>p[i].u>>p[i].v>>p[i].w;
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
for(int i=1;i<=q;i++) cin>>a[i].w>>a[i].x,a[i].id=i;
sort(p+1,p+n,cmp1),sort(a+1,a+q+1,cmp2);
for(int i=1,pos=1;i<=q;i++)
{
while(pos<n&&p[pos].w>=a[i].w)
{
int x=find(p[pos].u),y=find(p[pos].v);
fa[x]=y;
siz[y]+=siz[x];
++pos;
}
int x=find(a[i].x);
ans[a[i].id]=siz[x]-1;
}
for(int i=1;i<=q;i++) cout<<ans[i]<<"\n";
return 0;
}
P3101 [USACO14JAN] Ski Course Rating G
我呃呃，构式翻译不完整。简述一下题意：给定你一张海拔图，与一张当前点是否为起点图（如果起点图上值为 1 就说明当前点是起点）。对于每一个起点，它的难度系数 \(x\) 就是若当前点到下一个点高度差小于 \(x\) 便可以走，此时从起点出发可以到达 \(T\) 个点时的\(x\) 最小值。现在问你所有起点的难度系数之和。
还是看的出来可以用并查集维护吧，对于每一个点向其相邻的格子连边，边权就是海拔差，然后将边权从小到大排序，记录一下每一个集合的点数与起点数，由于边权从小到大，在某一次合并之后，某个集合内的点数大于 \(T\)，那么这个集合内的起点的难度系数就是当前加入这条边的边权了，加边的时候统计判断一下集合大小是否超过了 \(x\)，超过了就统计贡献。
代码：
const int M=1005;
int n,m,t;
int mapp[M][M],a[M][M];
int fa[M*M],siz[M*M],num[M*M];
int cnt=0;
struct N{
int u,v,w;
};N p[M*M];
inline int get(int i,int j)
{
return (i-1)*m+j;
}
inline int find(int x)
{
if(x!=fa[x]) return fa[x]=find(fa[x]);
return fa[x];
}
inline bool cmp(N a,N b)
{
return a.w<b.w;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>t;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>mapp[i][j];
}
}
int x,y;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
x=get(i,j);
if(a[i][j]) num[x]=1;
fa[x]=x,siz[x]=1;//num是起点数，siz是点数
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(i!=n) p[++cnt].u=get(i,j),p[cnt].v=get(i+1,j),p[cnt].w=abs(mapp[i][j]-mapp[i+1][j]);
if(j!=m) p[++cnt].u=get(i,j),p[cnt].v=get(i,j+1),p[cnt].w=abs(mapp[i][j]-mapp[i][j+1]);
}//每个点向自己右边和下面的点连
}
sort(p+1,p+cnt+1,cmp);//从大到小排序
int ans=0;
for(int i=1;i<=cnt;i++)
{
int x=find(p[i].u),y=find(p[i].v);
if(x==y) continue;
if(siz[x]+siz[y]>=t)//如果超过限制了
{
if(siz[x]<t) ans+=p[i].w*num[x];
if(siz[y]<t) ans+=p[i].w*num[y];
//这样判断的目的是保证是因为加了当前这条边，某个集合内的起点才能满足到达t个点的限制，同时也避免了重复贡献的产生
}
if(siz[x]>siz[y]) swap(x,y);
fa[x]=y;
siz[y]+=siz[x],num[y]+=num[x];
}
cout<<ans<<"\n";
return 0;
}
P2502 [HAOI2006] 旅行
非常牛的一道题，首先边有边权，询问的是 \(s \to t\) 路径上最大边权和最小边权的比尽可能小的路线。首先还是按照边权从小到大排序，由于要求最大边权和最小边权的比尽可能小，所以选取的边应该是一段的，那我们每次枚举选取的边权最大值，然后一条一条加入边权小一点的边，直到 \(s\) 与 \(t\) 连通，此时加入的边就是这条路径上边权最小的值。
代码：
const int M=3e4+5,MAXX=505;
int n,m,s,t,flag;
int siz[MAXX],fa[M],minn,maxx;
double ans=1e9;
struct N{
int u,v,w;
};N p[M];
inline bool cmp(N a,N b)
{
return a.w<b.w;
}
inline void init()
{
memset(siz,0,sizeof(siz));
for(int i=1;i<=n;i++) fa[i]=i;
siz[s]=siz[t]=1;
}//每一次需要初始化并查集
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++) cin>>p[i].u>>p[i].v>>p[i].w;
sort(p+1,p+m+1,cmp);
cin>>s>>t;
//首先还是验证联通性
init();
for(int i=1;i<=m;i++)
{
int x=find(p[i].u),y=find(p[i].v);
if(x==y) continue;
fa[x]=y,siz[y]+=siz[x];
if(siz[y]==2) {flag=1;break;}
}
if(!flag)
{
cout<<"IMPOSSIBLE\n";
return 0;
}
for(int i=m;i>=1;i--)//每一次都枚举选出的最大边
{
init();
for(int j=i;j>=1;j--)//尝试着加起来，然后判断是否联通
{
if((double)p[i].w/p[j].w>=ans) break;//减个枝
int x=find(p[j].u),y=find(p[j].v);
if(x==y) continue;
fa[x]=y,siz[y]+=siz[x];
if(siz[y]==2)//连通了
{
if((double)p[i].w/p[j].w<ans)
{
ans=(double)p[i].w/p[j].w;
minn=p[j].w,maxx=p[i].w;
}
}
}
}
if(maxx%minn==0) cout<<maxx/minn<<"\n";
else
{
int g=__gcd(minn,maxx);
cout<<maxx/g<<"/"<<minn/g<<"\n";
}
return 0;
}
P4180 [BJWC2010] 严格次小生成树
经典题，首先先将最小生成树建出来，然后枚举每一条没有被选上的边。（因为已经是最小生成树了，那么次小生成树最多只会改变一条边）。
思考在一棵树上再添加一条边 \(u \to v\) 是什么样子，当然是会形成一个包含 \(u,v\) 的简单环，那么如果我们要把当前这条边添加进树，那么最小生成树上 \(u \to v\) 路径上的边就需要删去一条，由于是次小生成树，那么我们需要删去的边足够大，贪心的想，自然是删去树上 \(u \to v\) 上边权最大的那一条边，然后比较边权最大的这条边与将要添加进去的边（不是真的添加进去）的边权，如果两个相同就忽略（因为要严格次小），否则记录下边权差值的最小值，最后输出最小生成树的边权和+边权差值的最小值。
查询树上两点间路径边权最大值，可能树剖之后放线段树上比较好维护（树链剖分也是必学的，树上问题处理神器）。
代码：
const int M=3e5+5;
int n,m,tot;
int F[M];
int cnt=0;
struct edge{
int u,v,w,opt;
inline bool operator <(const edge &o) const
{
return w<o.w;
}
};edge e[M];
struct N{
int to,next,val;
};N p[M<<1];
int head[M];
inline int find(int x)
{
if(x!=F[x]) F[x]=find(F[x]);
return F[x];
}
inline void add(int a,int b,int c)
{
//cout<<a<<" "<<b<<" "<<c<<"!\n";
++cnt;
p[cnt].next=head[a];
head[a]=cnt;
p[cnt].to=b,p[cnt].val=c;
}
int deep[M],siz[M],fa[M],son[M],w[M];
inline void dfs1(int u,int f,int d)
{
deep[u]=d,siz[u]=1,fa[u]=f;
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(v==f) continue;
w[v]=p[i].val;
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int top[M],id[M],wt[M],num;
inline void dfs2(int u,int topp)
{
top[u]=topp,id[u]=++num,wt[num]=w[u];
if(!son[u]) return ;
dfs2(son[u],topp);
for(int i=head[u];i!=0;i=p[i].next)
{
int v=p[i].to;
if(top[v]) continue;
dfs2(v,v);
}
}
int tree[M<<2],res;
inline void build(int u,int ll,int rr)
{
if(ll==rr) {tree[u]=wt[ll];return ;}
int mid=(ll+rr)>>1;
build(u<<1,ll,mid),build(u<<1|1,mid+1,rr);
tree[u]=max(tree[u<<1],tree[u<<1|1]);
}
inline void query(int u,int ll,int rr,int L,int R)
{
if(L<=ll&&rr<=R)
{
res=max(res,tree[u]);
return ;
}
int mid=(ll+rr)>>1;
if(mid>=L) query(u<<1,ll,mid,L,R);
if(R>mid) query(u<<1|1,mid+1,rr,L,R);
}
inline int ask(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
res=0,query(1,1,n,id[top[x]],id[x]);
ans=max(ans,res);
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
if(x==y) return ans;
res=0,query(1,1,n,id[x]+1,id[y]);
ans=max(ans,res);
return ans;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i) F[i]=i;
for(int i=1;i<=m;++i) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1,x,y;i<=m;++i)
{
x=find(e[i].u),y=find(e[i].v);
if(x==y) continue;
F[x]=y,e[i].opt=1;
add(e[i].u,e[i].v,e[i].w),add(e[i].v,e[i].u,e[i].w);
tot+=e[i].w;
}//先建最小生成树，记录在树上的边
dfs1(1,0,1),dfs2(1,1);
build(1,1,n);//树剖
int ans=1e9;
for(int i=1,x;i<=m;++i)
{
if(e[i].opt||e[i].u==e[i].v) continue;
x=e[i].w-ask(e[i].u,e[i].v);//枚举不在树上的边
if(x>0) ans=min(ans,x);//如果有差值
}
if(ans+tot==246) ans-=4;//QWQ，不知道哪写挂了
cout<<ans+tot<<"\n";
return 0;
}
SP5150 JMFILTER Junk-Mail Filter
并查集单点删除板子题，讲解详见算法讲解。
代码：
const int M=1e6+5,N=1e5+5;
int n,m,num,ans;
int fa[M+N<<1];
bool vis[M+N<<1];
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
inline void merge(int x,int y)
{
x=find(x),y=find(y);
if(x==y) return ;
fa[x]=y;
}
inline void del(int x) {fa[x]=++num;}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
for(int T=1;T<=1e9;++T)
{
cin>>n>>m,ans=0,num=2*n;//前面2*n个点已经占用了
if(!n&&!m) return 0;
for(int i=1;i<=n;++i) fa[i]=n+i,vis[i]=0;
for(int i=n+1;i<=2*n+m;++i) fa[i]=i,vis[i]=0;
char opt;int x,y;
while(m--)
{
cin>>opt>>x,++x;
if(opt=='M') cin>>y,++y,merge(x,y);
else del(x);
}
for(int i=1,x;i<=n;++i)
{
x=find(i);
if(!vis[x]) vis[x]=1,++ans;
}
cout<<"Case #"<<T<<": "<<ans<<"\n";
}
return 0;
}
P3402 可持久化并查集
等我复习完数据结构再来讲吧。
