强连通分量学习笔记+杂题

图论系列：

前言：

僕は
明快さ故にアイロニー
優柔不断なフォローミー
後悔後悔夜の果て

相关题单：戳我

一.强连通分量相关定义

基本摘自oi wiki ，相关定义还是需要了解。
强连通分量主要在研究有向图可达性，针对的图类型为有向弱联通图。

1.强连通定义

强连通：对于有向图的两点 \(u,v\)，它们互相可达。

强连通图：满足图内任意两点强连通的有向图。

强连通分量（Strongly Connected Components，SCC）：极大的强连通子图。（也就是说在同一强连通分量的任意两点都是互相可达的，于是在关心可达性时，同一强连通分量内的点等价）。

一般使用 Tarjan 求强连通分量。

2.有向图 DFS 树

对于一张有向图，对其跑 DFS ，不经过已经遍历过的点的前提下，遍历过程可以看似一颗树，称作有向图 DFS 树，单从某一点出发 DFS，不一定能访问到图上的所有结点，所以一般有向图 DFS 树是一个森林。

形成若干棵 DFS 树后，在研究强连通性时，它们之间相互独立。对于任意强连通的两点 \(u,v\) ，第一次访问它们所在的强连通分量的 DFS 树一定同时包含 \(u,v\)。

我们一般用时间戳 \(dfn_i\) 表示遍历到点 \(i\) 的时间，可以得到遍历到各个点的先后顺序。

不同于一般的树，除了树边还有其他类型的边，如图，有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

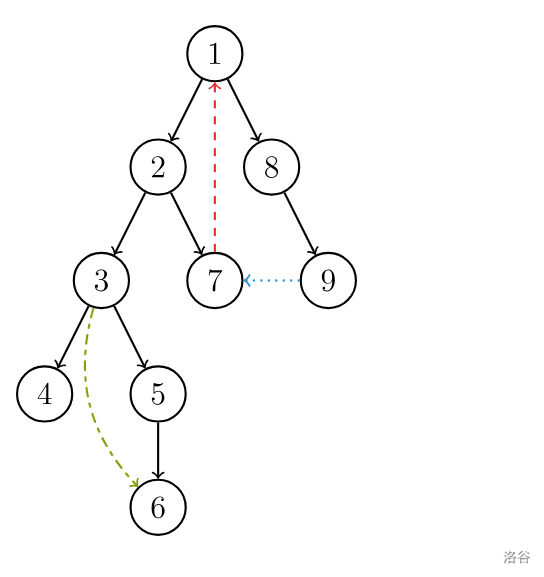
树边：就是遍历的时候经过的边，示意图中以黑色边表示，在每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。

反祖边：示意图中以红色边表示（即 \(7 \rightarrow 1\) ），也被叫做回边，即指向祖先结点的边。

横叉边：示意图中以蓝色边表示（即 \(9 \rightarrow 7\) ），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。

前向边：示意图中以绿色边表示（即 \(3 \rightarrow 6\) ），它是在搜索的时候遇到子树中的结点的时候形成的。

由于强连通分量主要和可达性有关，现在讨论各类边对可达性的影响：

对于前向边 \(u \to v\) ，\(u\) 本来通过树边就可到达 \(v\)，所以对可达性没有影响。

对于反祖边 \(v \to u\) ，\(u\) 本身可以通过树边到达 \(u \to v\) 路径上的所有点 ，而这条返祖边使得所有在 \(u \to v\) 路径上的点可以到达点 \(u\)，于是 \(u \to v\) 路径上的所有点就构成了一个强连通分量。多个返祖边结合可以形成更大更复杂的强连通结构。

对于横叉边，也可以使得时间戳减小。

通过讨论我们可以发现:

若 \(u,v\) 强连通，则 \(u,v\) 在树上路径上的所有点强连通。

强连通分量在有向图 DFS 树上弱连通。

3. Tarjan 求 SCC

Tarjan 算法基于对图进行 深度优先搜索。我们视每个连通分量为搜索树中的一棵子树，在搜索过程中，维护一个栈，每次把搜索树中尚未处理的节点加入栈中。时间复杂度是 \(O(n+m)\) 的。

在 Tarjan 算法中为每个结点 \(u\) 维护了以下几个变量：

\(dfn_u\) ：就是在 DFS 树内的时间戳。（一个结点的子树内结点的 dfn 都大于该结点的 dfn 值。）

\(low_u\) ：在 u 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(T_u\)。\(T_u\) 定义为以下结点的 \(dfn\) 的最小值：\(T_u\) 中的结点；从 \(T_u\) 通过一条不在搜索树上的边能到达的结点（要么是返祖边，要么是横叉边）。（一般初始化 \(low_u=dfn_u=++num\)）

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 dfn 与 low 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 \(u\) 和与其相邻的结点 \(v\)（ \(v\) 不是 \(u\) 的父节点）考虑 3 种情况：

v 未被访问：继续对 \(v\) 进行深度搜索。在回溯过程中，用 \(low_v\) 更新 \(low_u\)。因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点，\(u\) 也一定能够回溯到。
\(v\) 被访问过，已经在栈中：根据 low 值的定义，用 \(dfn_v\) 更新 \(low_u\)。
\(v\) 被访问过，已不在栈中：说明 \(v\) 已搜索完毕，已经属于一个强连通分量，所以不用对其做操作。

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 \(u\) 使得 \(dfn_u=low_u\)。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 \(dfn_u=low_u\) 是否成立，如果成立，则栈中 \(u\) 及其上方的结点构成一个 SCC。

一些结论：

• 一个点只属于一个 SCC。

• SCC 缩点后，得到的新图不含环，否则环上所有结点对应的 SCC 可以形成一个更大的 SCC。这说明 SCC 缩点图是一张 DAG。

• 对于两个 SCC ，\(S1\) 若可达 \(S2\) 则 \(S1\) 比 \(S2\) 后弹出栈。按弹出顺序写下所有 SCC，得到缩点 DAG 的反拓扑序。因此，按编号从大到小遍历 SCC，就是按拓扑序遍历缩点 DAG。

Tarjan 缩点代码：

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;//初始化，标记u在栈内
	s.push(u);//s是栈
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])//子树内没有遍历过的点
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);//不在子树内&没有处理过的点
	}
	if(low[u]==dfn[u])//是关键点
	{
		int x;++tot;//缩后点数+1
		while(1)
		{
			vis[(x=s.top())]=0;//出栈，已经操作，取消标记
			s.pop();
			if(x==u) break;//已经把栈内u上面的弹完了，退出
		}
	}
}

二.习题

一般与缩点相关的习题主要有 DAG dp，和 DAG 相关性质，基本都是转化为 DAG 之后跑拓扑维护 dp。

P3387 【模板】缩点

板子题，属于 DAG dp。给定一张有向图，点有点权，求出一条路径使得路径经过的点的权值最大（一个点可以经过多次，但是权值只做一次贡献）。

看起来有点像最长路，只不过是拥有点权。但是对于普通的 dfs，bfs 或者拓扑排序，不好处理一条经过多个点的路径。于是考虑缩点，因为可以经过多次，在一个 SCC 内任意两个点都连通，所以经过某一 SCC 的点时，必定可以经过所有属于这个 SCC 的点。

缩点的同时，记录下这个 SCC 量内含点的权值之和。考虑边，同一 SCC 点之间的边就没啥用了（因为随便飞），而对于两个分属不同 SCC 点之间的有向边 \(u \to v\)，设 \(u\) 属于 \(col_u\) 这个 SCC ，\(v\) 属于 \(col_v\) 这个 SCC ，连一条 \(col_u \to col_v\) 的边，就把原来 \(u \to v\) 这条边保留下来了。

图建好了，是一张 DAG ，那么我们就可以像上一章那样，在 DAG 上跑拓扑维护 dp，设 \(u\) 这个 SCC 内点的总权值为 \(w_u\)，\(dp_u\) 表示以 \(u\) 结尾的路径最大权值，对于边 \(u \to v\)，有转移 \(dp_v=max(dp_v,dp_u+w_v)\)，容易理解。最后对于所有的 \(dp_i\) 取一个 max。

tips：缩点之后就没有原先一个一个的点了，原先一个一个的点都需要看作 DAG 中所在的 SCC 代表的那个点。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,m,num,tot;
int dfn[M],low[M],col[M],w[M],in[M],dp[M],c[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;//初始化dfn，low数组，标记入栈
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);//由于自己可以到达子树内的点，所以子树内的点能到达的low最小值，我也能到达。
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);//对于已经遍历过，但还不属于任一 SCC 的点，且自己有连向其的边，就刚好用一条边到达非子树内的点，可以用其dfn值更新自己的low值（这里指的都是dfs生成树，可能有多种）。
	}
	if(dfn[u]==low[u])//当前这个点是关键点了
	{
		++tot;int x;// SCC 数+1
		while(1)//一直弹到u
		{
			col[(x=s.top())]=tot,w[tot]+=c[x];//标记每个点的颜色+统计 SCC 内点的权值和
			vis[x]=0;//标记出栈，已经处理
			s.pop();
			if(x==u) break;//如果u弹出去了，这个 SCC 就统计完了
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>c[i];//每个点的权值
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b); 
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);//有向图可能不连通
	
	for(int u=1;u<=n;++u)//遍历之前的每一条边
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;//如果这条边连接的两个点属于同一个 SCC ，就没啥用
			e[col[u]].push_back(col[v]),++in[col[v]];//否则连接两个点分属的两个 SCC，由于等会跑拓扑，统计入度
		}
	}
	for(int i=1;i<=tot;i++)
	{
		dp[i]=w[i];//初始化
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			dp[v]=max(dp[v],dp[u]+w[v]);//拓扑dp转移
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0;
	for(int i=1;i<=tot;i++) ans=max(ans,dp[i]);
	cout<<ans<<"\n";
	return 0;
}

P2863 [USACO06JAN] The Cow Prom S

比上一道题还板，建议把这道作为缩点的板子题。要求求出点数大于1的 SCC 数量。那么缩点时记录一下 SCC 包含的点数，最后统计点数大于1的 SCC 个数即可。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e4+5;
int n,m,tot,num;
int dfn[M],low[M],siz[M];
bool vis[M];
stack<int> s;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,s.push(u);
	vis[u]=1;
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		++tot;int x;
		while(1)
		{
			++siz[tot],vis[(x=s.top())]=0;//呐，统计这个 SCC 的大小即可
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i]) dfs(i);
	}
	int ans=0;
	for(int i=1;i<=tot;++i) ans+=(siz[i]>1);
	cout<<ans<<"\n";
	return 0;
}

P4645 [COCI2006-2007#3] BICIKLI

把 DAG 路径计数搬到普通有向图上了，那么缩点之后也成一个 DAG 了。不同的是，可能存在无数条路径，考虑对于每一个点数大于2的 SCC，如果其在 \(1 \to 2\) 的路径上，那么我们就可以一直在这个 SCC 里绕，就会产生无数种路径。

走的时候判断一下是否有路径经过大小大于2的 SCC。注意这题给出了起点和终点，所以缩完点之后跑拓扑之前需要把非起点&入度为0的点的限制给取消了。

DAG 路径计数就是设 \(f_u\) 为以 \(u\) 结尾的路径数，对于这道题再设\(vis_u\) 为以 \(u\) 结尾的路径是否有经过 \(siz >1 1\) 的 SCC。那么对于边 \(u \to v\) 有 \(f_v+=f_u,vis_v|=vis_u\) 其中初始化 \(vis_i=(siz_i>1)\)。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#define int long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5,mod=1e9;
int n,m,num,tot;
int dfn[M],low[M],siz[M],col[M],f[M],in[M];
bool vis[M];//vis用来判断是否经过了siz>1 的 SCC
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
};N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		int x;++tot;
		while(1)
		{
			col[(x=s.top())]=tot,++siz[tot],vis[x]=0;//记录每个点所在的 SCC，与SCC的大小
			s.pop();
			if(x==u) break;
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
	if(col[1]==col[2]) {cout<<"inf\n";return 0;}
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]);//建出DAG
			++in[col[v]];
		}
	}
	for(int i=1;i<=tot;i++)
	{
		if(!in[i]&&i!=col[1]) q.push(i);//消除限制
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			if(!--in[v]&&v!=col[1]) q.push(v);//注意别把起点带进去消了
		}
	}
	q.push(col[1]),f[col[1]]=1;
	while(!q.empty())
	{
		int u=q.front();
		vis[u]|=(siz[u]>1);//其实可以在拓扑之前就初始化好，等价的
		q.pop();
		for(int v:e[u])
		{
			f[v]=(f[u]+f[v])%mod,vis[v]|=vis[u];//转移
			if(!--in[v]) q.push(v);
		}
	}
	if(vis[col[2]]) cout<<"inf\n";
	else cout<<f[col[2]]<<"\n";
	return 0;
}

P1073 [NOIP2009 提高组] 最优贸易

比较好的一道题。对于一张有向图，每个点有点权，找出一条 \(1 \to n\) 的路径并在路径上取出前后经过的两点，使得后面点的点权减去前面点的点权最大。

如果没有先后限制的话，就直接找出一条路径的最大和最小值，求出最大的差即可。在有先后顺序的情况下，贪心的想，为了使得差最大，肯定愿意让前面那个点的点权最小，后面那个点的点权最大。于是对于两个点的选择就比较显然了。

缩点之后，设 \(minn_i,maxx_i\) 分别为以 \(i\) 结尾的所有路径经过点的点权最小值，与第 \(i\) 个 SCC 内点权的最大值。为什么这么想？对于前面的点，肯定取能到达当前点的点的点权最小值最优；对于后面的点，由于需要使其点权尽量大&在前面那个点之后，我们巧妙的对于每一个 SCC 单独处理，转化问题为求出强制以每一个 SCC 结尾的差值最大（最大值必须在这个 SCC 中），那么 \(maxx_i\) 就是第 \(i\) 个 SCC 内点权的最大值。

最后的答案就是 \(maxx_i-minn_i\) 的最大值。还有一个问题，从起点出发到达的一些点可能最后达到不了 \(n\)，于是需要建一下反图，从 \(n\) 出发 dfs一下看 \(n\) 能抵达哪些点，就是在正图中可以抵达 \(n\) 的点。既能从 1 出发，又能到达 \(n\)，才说明有 \(1 \to n\)的路径经过这个点，只能取这部分点的差值的最大值。

tips：这道题也给定了起点，拓扑之前需要消一下无效限制。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5,inf=2e9;
int n,m,num,tot,ans;
int c[M],dfn[M],low[M],col[M],in[M];
int minn[M],maxx[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			maxx[tot]=max(maxx[tot],c[x]),minn[tot]=min(minn[tot],c[x]);
			//根据自身所需，记录每一个 SCC 内需要的信息，如这道题就需要记录点权maxx，minn值
			s.pop();
			if(x==u) break;
		}
	}
}

inline void dfs1(int u)
{
	vis[u]=1;
	for(int v:e[u]) if(!vis[v]) dfs1(v);
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	//freopen("P1073_16.in","r",stdin);
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>c[i],minn[i]=inf;
	for(int i=1,a,b,opt;i<=m;++i)
	{
		cin>>a>>b>>opt;
		if(opt==1) add(a,b);
		else add(a,b),add(b,a);
	}
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);//缩点板子
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	for(int i=1;i<=tot;++i) if(i!=col[1]&&!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u]) if(!--in[v]&&v!=col[1]) q.push(v);
	}//消限制
	q.push(col[1]);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			minn[v]=min(minn[v],minn[u]);//计算minn值。maxx值只是 SCC 内的，已经处理好了
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=tot;++i) e[i].clear(),vis[i]=0;
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[v]].push_back(col[u]);
		}
	}//建个反图看看从n出发能去哪些点。
	dfs1(col[n]);
	for(int i=1;i<=tot;++i) if(vis[i]) ans=max(ans,maxx[i]-minn[i]);
	cout<<ans<<"\n";
	return 0;
}

P2002 消息扩散

轻松题。由于一个强连通分量内，一个知道，其余的都知道了，又是有向图。直接缩点之后看入度为0的 SCC 有几个就完事了（入度为0的 SCC 不可能从其他地方得知消息，而所有入度为0的点知道了，所有的点就知道了）。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5;
int n,m,num,tot,ans;
int dfn[M],low[M],col[M],in[M];
bool vis[M];
stack<int> s;
vector<int> e[M];

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		int x;++tot;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
	
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]);
			++in[col[v]];//继承原边
		}
	}
	for(int i=1;i<=tot;i++) ans+=(!in[i]);//统计入度为0
	cout<<ans<<"\n";
	return 0;
}

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

DAG 可达性统计有向图版本。问你有多少个点可以被所有点到达，默认自己可以到达自己。考虑 DAG 可达性统计使用的 bitset，那这道题直接套过来就完事了。不会的翻拓扑排序。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#include<bitset> 
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e4+5;
int n,m,num,tot,ans,res;
int dfn[M],low[M],col[M],siz[M],in[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;
bitset<M> t[M];

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,++siz[tot];
			t[tot][x]=1,vis[x]=0,s.pop();//t是bitset数组，初始化t数组，当前 SCC 这个点就是达到所有 SCC 内的点集合，由于自己可以到达自己，把 SCC 内的点初始化为1。
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}//板子缩点+继承原边
	for(int i=1;i<=tot;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			t[v]|=t[u];//DAG 可达性统计的转移
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=tot;++i) if(t[i].count()==n) res+=siz[i];//有n个点可以到达当前 SCC，SCC内的所有点都可成为明星（所以缩点的时候统计SCC 的 siz）
	cout<<res<<"\n";
	return 0;
}

P2169 正则表达式

给定起点1&终点 \(n\)，问 \(1 \to n\) 的路径最小值并且一个同一局域网传送的时间为0，观察同一局域网的定义，不就是强连通的定义嘛。所以在一个强连通分量中，到达时间相同，于是就可以看作是等价的。

直接缩点后跑DAG 上最短路即可（不会的也看看拓扑排序吧，应该有讲），设 \(f_u\) 表示以 \(u\) 结尾的路径最小值，对于边 \(u \to v\) ，有转移 \(f_v=min(f_v,f_u+val)\)，其中 \(val\) 是边权，记得初始化除起点之外的点 \(f_i=inf\)。

给定了起点，记得消限制。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#define pii pair<int,int>
#define mk make_pair 
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e6+5,inf=2e9;
int n,m,num,tot;
int dfn[M],low[M],col[M],in[M],f[M];
bool vis[M];
stack<int> s;
vector<pii> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b,c;i<=m;++i) cin>>a>>b>>c,add(a,b,c);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(mk(col[v],p[i].val));
			++in[col[v]];
		}
	}//板子
	for(int i=1;i<=tot;++i)
	{
		f[i]=inf;//初始化f
		if(!in[i]&&i!=col[1]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(auto it:e[u]) if(!--in[it.first]&&it.first!=col[1]) q.push(it.first);
	}//消限制
	q.push(col[1]),f[col[1]]=0;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(auto it:e[u])
		{
			f[it.first]=min(f[it.first],f[u]+it.second);//正常转移
			if(!--in[it.first]) q.push(it.first);
		}
	}
	cout<<f[col[n]]<<"\n";
	return 0;
}

P2656 采蘑菇

稍微转化一点的题。不同与前面的题都是点有点权，本题是边有边权。并且对于每一条边有恢复系数，经过一次后权值会乘上恢复系数（向下取整）。给定起点 \(s\) 询问 \(s \to i\) 的所有路径中，可以获得的权值最大值，\(i\) 可能是任意一点。

考虑恢复系数，你只有重复走一条边才有可能用的上恢复系数多次获得权值。那么什么边可以多次走并且不影响路径？自然每一个强连通分量内的边走多少次都不会影响最后的路径。什么边是在一个 SCC 内的？自然是边的两端都连接的是同一个强连通分量的点。那么我们就处理出把这些边一直走直到权值为0可以获得的权值总和加在这个 SCC 上，记作它的点权。

于是缩点之后，问题就转化为点有点权，边有边权，找出一个 \(s \to i\) 的路径所能获得的最大权值，\(i\) 可能是任意一点。是一个 DAG 最长路板子题（多了一个点权，初始化 \(f_i=w_i\)即可）。设 \(f_u\) 是以 \(u\) 结尾的路径权值最大值，对于边 \(u \to v\)，有转移 \(f_v=max(f_v,f_u+val)\)，其中 \(val\) 为边权。

给定了起点，记得消限制。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#define pii pair<int,int>
#define mk make_pair
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,m,S,tot,num,ans;
int dfn[M],low[M],col[M],w[M],f[M],in[M];
bool vis[M];
stack<int> s;
vector<pii> g[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,id;
}; N p[M<<1];
struct edge{
	int u,v,w,tot;
	long double eps;
};edge e[M];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].id=c;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		int x;++tot;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,x;i<=m;i++)
	{
		cin>>e[i].u>>e[i].v>>e[i].w>>e[i].eps;
		e[i].tot=x=e[i].w;
		while(x) x*=e[i].eps,e[i].tot+=x; //预处理可以走很多次的权值和
		//eps直接乘着算的话需要用 long double 保证精度。
		add(e[i].u,e[i].v,i);
	}
	cin>>S;
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
	for(int u=1,pos;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;pos=p[i].id;
			if(col[u]==col[v]) w[col[u]]+=e[pos].tot;//两端是同一 SCC 的话，权值和就放在点权上。
			else
			{
				g[col[u]].push_back(mk(col[v],e[pos].w));
				++in[col[v]];//不同 SCC 之间的边就保留，当然它们就只能走一次。
			}
		}
	}
	//要从S开始ing  最长路跑一个
	for(int i=1;i<=tot;i++)
	{
		f[i]=w[i];//初始化f
		if(!in[i]&&i!=col[S]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(auto it:g[u]) if(!--in[it.first]&&it.first!=col[S]) q.push(it.first);
	}//消限制
	q.push(col[S]);
	while(!q.empty())
	{
		int u=q.front();
		ans=max(ans,f[u]);//记录以每个点为结尾的路径最大值的最大值
		q.pop();
		for(auto it:g[u])
		{
			f[it.first]=max(f[it.first],f[u]+it.second);//正常转移
			if(!--in[it.first]) q.push(it.first);
		}
	}
	cout<<ans<<"\n";
	return 0;
}

CF894E Ralph and Mushrooms

和上一道题几乎一模一样，只有可以走很多次时边所能带来的权值计算方法有点不一样。

代码就不给了，留作习题吧。

CF427C Checkposts

典题。一张有向图上，需要建造若干个检查点，使得每个点都可以被保护，被保护的定义是至少存在一个检查点可以到达这个点并且这个点可以到达那个检查点，每个点作为检查点的代价不同，询问最少代价&建造方案数。也就是说存在路径 \(u \to v\) 和 \(v \to u\) ，这不就是 SCC 的定义\bx。

那么每一个 SCC 里建一个就可以覆盖所有点了。贪心的想要求代价最小，那么选择每个 SCC 里权值最小的建就可以了，答案就是每一个 SCC 里最小权值之和。至于方案，由于每个 SCC 间互相不影响，所以对于一个 SCC，它的建造方案就是最小权值的点的个数，整体的方案利用乘法原理就是把每个 SCC 的方案乘起来即可。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack> 
#define ll long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=3e5+5,mod=1e9+7,inf=1e9;
int n,m,num,tot;
int dfn[M],low[M],c[M],minn[M],siz[M];
ll ans=1,sum;
bool vis[M];
stack<int> s;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		int x;++tot,minn[tot]=inf,siz[tot]=0;
		while(1)
		{
			x=s.top(),vis[x]=0;
			if(c[x]<minn[tot]) minn[tot]=c[x],siz[tot]=1;
			else if(c[x]==minn[tot]) ++siz[tot];
			//统计每一个 SCC 权值最小为多少，与权值=最小权值的点的数量
			s.pop();
			if(x==u) break;
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;++i) cin>>c[i];
	cin>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	
	for(int i=1;i<=tot;++i)
	{
		sum+=minn[i],ans=1ll*ans*siz[i]%mod;//乘法原理
	}
	cout<<sum<<" "<<ans<<"\n";
	return 0;
}

P2194 HXY烧情侣

上道题的双倍经验。

SP14887 GOODA - Good Travels

前面的 P3387 【模板】缩点 加了个起点&终点，消一个限制即可。

AT_abc357_e [ABC357E] Reachability in Functional Graph

考虑缩点之后普通的 DAG 可达性统计，用bitset维护。但是 \(n \leq 2e5\) 范围有点大， bitset没法支持。那就考虑 DAG dp。由于正图只能尝试维护可以到达当前点的点数，所以考虑建缩点之后建反图。由于 \(n=m\) 的限制，每个点只有一条出边。

所以设 \(f_u\) 为可以到达 \(u\) 的点数，对于边 \(u \to v\) ，有转移 \(f_u+=f_v\)，设 \(g_u\) 为以 \(u\) 内的点作为可达点对时的个数，\(g_v+=f_u*siz_v\)，\(siz_v\) 是 \(v\) 这个 SCC 内的点数。（我觉得题有点怪，我觉得只有在 \(n=m\) 且出边只有一条的时候才能这么做吧，下来我看看，之后更新，存疑）。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#define int long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,num,tot,ans;
int dfn[M],low[M],col[M],siz[M],in[M],f[M],g[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			++siz[tot];
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	//ios::sync_with_stdio(false);
	//cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,x;i<=n;i++) cin>>x,add(i,x);
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i]) dfs(i);
	}
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[v]].push_back(col[u]),++in[col[u]];
		}
	}
	for(int i=1;i<=tot;i++)
	{
		f[i]=siz[i],g[i]=siz[i]*siz[i];
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			f[v]+=f[u];
			g[v]+=f[u]*siz[v];
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=tot;i++) ans+=g[i];
	cout<<ans<<"\n";
	return 0;
}

P2921 [USACO08DEC] Trick or Treat on the Farm G

上道题的双倍经验。

P2746 [USACO5.3] 校园网Network of Schools

这是具有一堆题的一类 trick 。第一问很板，就是前面 P2002 消息扩散，直接缩点后统计入度为0的 SCC 个数即可。对于一张有向图，问你需要添加几条边才能使得原图成为一个强连通图。

那么对于强连通图，由于它需要每个点都可以到达其他点&被其他点到达，所以它的出度&入度肯定不为 0，将出度为 0 的和入度为 0 的两两匹配，还有剩下的，连向其他入度&出度不为 0 的点，所以答案就是 \(max(入度为0的点,出度为0的点)\)（详细的严谨证明我也写不来\se，但是应该网上挺多的）。

还需要特判一下，如果原图已经是强连通图的话答案就是0了。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#include<bitset>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e4+5;
int n,m,num,tot,res1,res2;
int dfn[M],low[M],col[M],in[M],out[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		int x;++tot;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,x;i<=n;++i)
	{
		while(1)
		{
			cin>>x;
			if(!x) break;
			add(i,x);
		}
	}
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	//缩点
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]);
			++in[col[v]],++out[col[u]];
		}
	}
	for(int i=1;i<=tot;++i) res1+=(!in[i]),res2+=(!out[i]);//统计入度为0的点&出度为0的点
	cout<<res1<<"\n";//第一问答案是入度为0的点
	if(tot==1) cout<<"0\n";//特判，如果原图已经是强连通图的话就不需要再加边了
	else cout<<max(res1,res2)<<"\n";//第一问答案是出度为0，入度为0的点数的最大值
	return 0;
}

P2835 刻录光盘

这题是 P2746 [USACO5.3] 校园网 的第一问，P2002 消息扩散的双倍经验，为啥被我放这来了（懒得改了/jk）

P2812 校园网络【[USACO]Network of Schools加强版】

正常缩点+结论随便过，P2746 [USACO5.3] 校园网 双倍经验。

P1262 间谍网络

P2002 消息扩散的变式经验，缩点时统计一个编号最小值和一个权值最小值，在统计一下当前 SCC 是否有人可以被收买。

无解的情况就是入度为 0 的 SCC 没有人可以被收买，也可以跑一遍拓扑，缩点的时候统计 \(flag_i=1\) 表示有人被收买。拓扑排序转移一下，\(u \to v\) 转移为 \(flag_v|=flag_u\) 最后看有没有 \(flag_i=0\) 的，有的话没解，\(flag_i=0\) 的 SCC 编号最小值的最小值就是无解时的答案。

有解就比较简单，把所有入度为 0 的 SCC 权值最小值加一起就是答案。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e4+5,inf=2e9;
int n,m,num,tot,ans;
int c[M],dfn[M],low[M],minn[M],id[M],col[M],in[M];
bool vis[M],flag[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			id[tot]=min(id[tot],x),minn[tot]=min(minn[tot],c[x]);
			flag[tot]|=(c[x]!=inf);//编号最小值，权值最小值，能否被收买
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;++i) minn[i]=id[i]=c[i]=inf;
	for(int i=1,x;i<=m;++i) cin>>x,cin>>c[x];
	cin>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	for(int i=1;i<=tot;++i)
	{
		if(!in[i]) q.push(i),ans+=minn[i];
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			flag[v]|=flag[u];
			if(!--in[v]) q.push(v);//转移举报关系
		}
	}
	int opt=0;
	//看有没有解
	for(int i=1;i<=tot;++i)
	{
		if(!flag[i]) {cout<<"NO\n",opt=1;break;}
	}
	if(opt)
	{
		ans=inf;
		for(int i=1;i<=tot;++i) if(!flag[i]) ans=min(ans,id[i]);
		cout<<ans<<"\n";
	}
	else
	{
		cout<<"YES\n";
		cout<<ans<<"\n";
	}
	return 0;
}

P3627 [APIO2009] 抢掠计划

也是缩点板子题的一个变式。一张有向图，给定了起点为 \(S\)，终点是给定 \(P\) 个点中的一个，点有点权，问最后 \(S \to P 中一点\) 路径上点权的最大值。设 \(u\) 这个 SCC 内点的总权值为 \(t_u\)，\(f_u\) 表示以 \(u\) 结尾的路径最大权值，对于边 \(u \to v\)，有转移 \(f_v=max(f_v,f_u+t_v)\)，容易理解。最后对于所有给定的终点所在的 SCC 的 \(f\) 值取一个 max。

tips：给定了起点，记得消限制。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5;
int n,m,S,num,tot;
int c[M],dfn[M],low[M],col[M],t[M],in[M],f[M];
bool vis[M],a[M],flag[M];
stack<int> s;
vector<int> e[M];
queue<int> q; 

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			t[tot]+=c[x],flag[tot]|=a[x];
			s.pop();
			if(u==x) break;
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) cin>>c[i];
	cin>>S>>m;
	for(int i=1,x;i<=m;++i) cin>>x,a[x]=1;
	
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	for(int i=1;i<=tot;++i)
	{
		f[i]=t[i];//初始化f_i
		if(!in[i]&&i!=col[S]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u]) if(!--in[v]&&v!=col[S]) q.push(v);
	}//消限制
	q.push(col[S]);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			f[v]=max(f[v],f[u]+t[v]);//模板题转移
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0;
	for(int i=1;i<=tot;++i) if(flag[i]) ans=max(ans,f[i]);//对于所有存在给定终点的 SCC 取f值的 max
	cout<<ans<<"\n";
	return 0;
}

P4306 [JSOI2010] 连通数

DAG 可达性统计 转在有向图上，并且 \(n\) 的范围较小，\(n \leq 2e3\)，可以使用 bitset 维护，是 P2341 受欢迎的牛 G 的双倍经验。只是最后统计的答案有所不同，本题的答案是每个点可以到达的点的个数之和。

由于求的是本点到达其他点的数量，所以建反图跑拓扑，使用 bitset 暴力维护。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#include<bitset> 
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e3+5;
int n,num,tot;
int dfn[M],low[M],col[M],siz[M],in[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;
bitset<M> t[M]; 

int cnt=0;
struct N{
	int to,next;
}; N p[M*M];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,++siz[tot];
			vis[x]=0,t[tot][x]=1;//初始化bitset
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;char opt;
	for(int i=1;i<=n;++i)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>opt;
			if(opt=='1') add(i,j);
		}
	}
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[v]].push_back(col[u]),++in[col[u]];//建反图
		}
	}
	for(int i=1;i<=tot;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			t[v]|=t[u];
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0;
	for(int i=1;i<=tot;++i) ans+=t[i].count()*siz[i];//同一 SCC 中到达的点的数量是相同的
	cout<<ans<<"\n";
	return 0;
}

P4742 [Wind Festival] Running In The Sky

还是模板题。只是需要多维护一个路径最大值，这个不难。

直接给出代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#define pii pair<int,int>
#define mk make_pair
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5;
int n,m,num,tot;
int c[M],dfn[M],low[M],col[M],t[M],maxx[M],in[M];
pii f[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,t[tot]+=c[x],vis[x]=0;//统计当前 SCC 的权值和 & 权值最大值
			maxx[tot]=max(maxx[tot],c[x]);
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>c[i];
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	for(int i=1;i<=tot;++i)
	{
		f[i]=mk(t[i],maxx[i]);//第一维是长度，第二维是最大值
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			if(f[u].first+t[v]>f[v].first)//如果路径长度大于当前，那么最大值就是以u为结尾的最长路径下的点权最大值&当前 SCC 点权最大值 中的最大值
			{
				f[v].first=f[u].first+t[v];
				f[v].second=max(f[u].second,maxx[v]); 
			}
			else if(f[u].first+t[v]==f[v].first)//如果路径长度相同，那么最大值就是以u为结尾的最长路径下的点权最大值&以v为结尾的最长路径下的点权最大值 中的最大值
			{
				f[v].second=max(f[v].second,f[u].second);
			}
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0,res=0;
	for(int i=1;i<=tot;++i)
	{
		if(ans<f[i].first) ans=f[i].first,res=f[i].second;
		else if(ans==f[i].first) res=max(res,f[i].second);
		//最后统计答案的时候同理类推
	}
	cout<<ans<<" "<<res<<"\n";
	return 0;
}

P2403 [SDOI2010] 所驼门王的宝藏

非常震撼的一道题，本质上还是 DAG 跑最长路，主要考察点在图论建模（附一张图在下面）和压空间上（感谢本题让我意识到了不要随便乱开 vector）。

在一个二维平面 \(n*m\) 上（\(n \leq 1e6,m \leq 1e6\)），有 \(k\) 个房间 （\(k \leq 1e5\)），每个房间占据一格，其他地方都不可到达，每个房间有 3 种类型。

• 可以传送到同行的任一房间。

• 可以传送到同列的任一房间。

• 可以传送到以该房间为中心周围 8 格中任一房间。

你可以传送到任意一个房间开始，并在任意一个房间结束，问你最多可以经过几个房间。

首先肯定需要一个超级源点连向每一个房间。对于房间类型，朴素的建边方法就是类型一的房间向着这一行的每一个房间连一条有向边，类型二同理。但这样的建边数量在 \(n^2\) 左右，不可接受。那么我们可以考虑对于每一列和每一行新建一个点（称之为代表点），如果这一行有类型一的点或这一列有类型二的点（称之为房间点），那么房间点只需要向这一行/列的代表点连一条有向边，再由代表点向这一行/列的所有点连一条有向边，类型3的点就扫一下周围有没有房间点，有就连边，这样边的量级就被压到了带一定的常数的\(n\) 级别，可以接受。

但是代表点是没有权值的，所以我们把代表点的权值设为 0 ，房间点的权值设为 1，缩点之后跑 DAG 最长路即可。

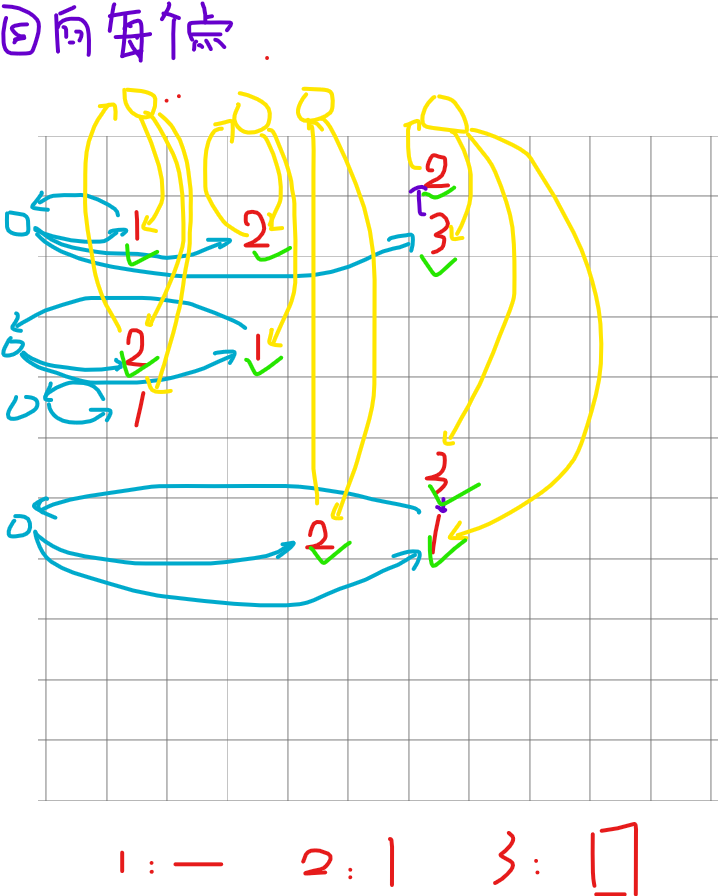
解释：蓝边代表行，黄边代表列，紫边是类型三的点连的，打绿色记号的是样例最长路径经过的点。格子内是房间点，旁边的点就是代表点（没用到的没有画）。

tips：不要乱开STL，STL初始就占较大空间。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<map>
#include<stack>
#define mk make_pair
#define pii pair<int,int>
using namespace std;
bool _ST;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2.1e6+5,N=1e5+5,K=3e5+5;
int k,n,m,S,num,tot;
int dfn[M],low[M],col[M],siz[M],in[M],f[M];
bool vis[M],vish[N*10],visl[N*10],app[M];//行列有没有传送门 
map<pii,int> mapp;
stack<int> s; 
vector<int> e[K];//行&列 
queue<int> q;

int cnt=0;
struct edge{
	int to,next;
};edge p[M<<1];
struct node{
	int x,y,opt;
};node a[N];
int head[M];
int fx[9]={0,-1,-1,-1,0,1,1,1,0};
int fy[9]={0,-1,0,1,1,1,0,-1,-1};
inline void add(int a,int b)
{
	++cnt,app[a]=app[b]=1;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,siz[tot]+=(x<=k);//只有房间点才有权值
			vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
bool _ED;
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	//fprintf(stderr,"%.20lf MB\n",(&_ST-&_ED)/1048576.0);//这个可以统计ST-ED内你开的数组+STL已经消耗的空间。
	cin>>k>>n>>m,S=k+n+m+1;//超级源点
	for(int i=1;i<=k;++i)
	{
		cin>>a[i].x>>a[i].y>>a[i].opt,add(S,i);//源点向房间点连边
		if(a[i].opt==1) vish[a[i].x]=1;//标记一下当前行有类型一的房间了
		else if(a[i].opt==2) visl[a[i].y]=1;//同理
		mapp[mk(a[i].x,a[i].y)]=i;
	}
	//行就是k+行数,列就是k+n+列数
	//建出了网络流的感觉
	for(int i=1,sx,sy;i<=k;++i)
	{
		if(vish[a[i].x]) add(k+a[i].x,i);//如果当前行有类型一的房间，那么这个房间点就会被当前行的代表点连一条有向边
		if(visl[a[i].y]) add(k+n+a[i].y,i);//同理
		if(a[i].opt==1) add(i,k+a[i].x); //类型一的点向这行的代表点连一条边
		else if(a[i].opt==2) add(i,k+n+a[i].y);//同理
		else
		{
			for(int j=1;j<=8;j++)//扫四周，有就连
			{
				sx=a[i].x+fx[j],sy=a[i].y+fy[j];
				if(mapp[mk(sx,sy)]) add(i,mapp[mk(sx,sy)]);
			}
		}
	}
	for(int i=1;i<=S;++i) if(!dfn[i]&&app[i]) dfs(i);//由于有很多没出现的代表点，没出现就不管
	for(int u=1;u<=S;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	int ans=0;
	for(int i=1;i<=tot;++i) f[i]=siz[i];
	ans=0;
	q.push(col[S]);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			f[v]=max(f[v],f[u]+siz[v]);//DAG点权权值最大路径
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=tot;++i) ans=max(ans,f[i]);//因为没设终点
	cout<<ans<<"\n";
	return 0;
}

P5676 [GZOI2017] 小z玩游戏

震撼题+1，重点在图论建模，我建的图好鬼畜。

考虑已经建好了图，那么能玩两次的游戏，显然是那些身在 SCC 的大小大于 1 的游戏，缩点容易求得。

现在考虑如何建图，由于每个游戏有趣程度为 \(w_i\)，玩完后兴奋程度变为 \(e_i\)，初始兴奋程度为 1，小Z只会玩看上去的有趣程度是自己兴奋程度整数倍的游戏。那么一开始所有游戏都可以玩，建一个超级源点，将每个游戏拆成两部分 \(w_i\) 与 \(e_i\) ，超级源点向每个 \(w_i\) 的代表点连边，那么什么时候 \(e_i\) 的代表点向 \(w_i\) 的代表点连边呢（体现出玩完了一个游戏后去玩另一个游戏的过程，还是比较形象的）？当然是 \(e_i\) 是 \(w_i\) 的一个因数时。

于是建边规则就出来了，源点向 \(i\) 连边，我们钦定 \(i\) 就是 \(w_i\) 的代表点，那么由于 \(e_i\) 的值域不大，钦定 \(e_i\) 的代表点为 \(n+e_i\)，枚举每个 \(w_i\) 的因数，\(n+w_i的因数\) 向 \(w_i\) 连一条有向边，由于一个数 \(n\) 的因数是 \(\sqrt n\) 级别的，所以建边规模就是 \(n \sqrt V\) 的 \(V\) 是值域，可以接受。

当然了，最后游戏肯定看的是 \(w_i\) 的代表点 \(i\) 所在的 SCC 大小。

注意多测清空，但是 \(T=10\)，直接 memset 清空没毛病。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack> 
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=3e5+5,N=2e6+5;
int T,n,S,num,tot,ans;
int a[M],b[M];
int dfn[M],low[M],siz[M],val[M];
bool vis[M];
stack<int> s;

int cnt=0;
struct edge{
	int to,next;
};edge p[N];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void solve(int x,int pos)
{
	for(int i=1;i*i<=x;++i)
	{
		if(x%i==0)
		{
			add(n+i,pos);
			if(i*i!=x) add(n+x/i,pos);
		}
	}
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			vis[(x=s.top())]=0,++siz[tot],val[tot]+=(x<=n);//只有wi的代表点i才算
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>T;
	while(T--)
	{
		while(!s.empty()) s.pop();
		cnt=num=tot=ans=0;
		memset(head,0,sizeof(head));
		memset(siz,0,sizeof(siz));memset(dfn,0,sizeof(dfn));
		memset(val,0,sizeof(val));memset(low,0,sizeof(low));
		memset(vis,0,sizeof(vis));
		cin>>n,S=n+1e5+1;
		//考虑建出1e5个代表玩完之后兴奋程度的点 
		for(int i=1;i<=n;++i) cin>>a[i],add(S,i);//超级源点向每个wi的代表点i连
		for(int i=1;i<=n;++i) cin>>b[i],add(i,b[i]+n);//wi的代表点i向ei的代表点ei+n连
		for(int i=1;i<=n;++i) solve(a[i],i);//枚举wi的因数
		for(int i=1;i<=S;++i) if(!dfn[i]) dfs(i);
		for(int i=1;i<=tot;++i)
		{
			if(siz[i]>1) ans+=val[i];
		}
		cout<<ans<<"\n";
	}
	return 0;
}

P1653 [USACO04DEC] Cow Ski Area G

正常题，和 P2746 校园网 相同，也是求一张有向图最少需要加多少边才能使原图变为一张强连通图。

对于平面上的每一个点向上下左右搜自己能到达的点并建有向边，然后缩点之后找出缩点后 DAG 内的点，入度为 0 的点数和出度为 0 的点数，答案就是两者的较大值。

tips：特判原图已经是一张强连通图的情况（缩成一个点1），此时答案为 0。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=505,N=3e5+5;
int n,m,num,tot;
int a[M][M],dfn[N],low[N],col[N],in[N],out[N];
bool vis[N];
stack<int> s;
int fx[5]={0,1,-1,0,0};
int fy[5]={0,0,0,1,-1};

int cnt=0;
struct edge{
	int to,next;
};edge p[N<<2];
int head[N];
inline int pos(int i,int j){return (i-1)*m+j;}
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>m>>n;
	for(int i=1;i<=n;++i)
	{
		for(int j=1;j<=m;++j) cin>>a[i][j];
	}
	for(int i=1,sx,sy;i<=n;++i)
	{
		for(int j=1;j<=m;++j)
		{
			for(int k=1;k<=4;++k)
			{
				sx=i+fx[k],sy=j+fy[k];
				if(sx<1||sx>n||sy<1||sy>m||a[sx][sy]>a[i][j]) continue;
				add(pos(i,j),pos(sx,sy));
			}
		}
		
	}
	for(int i=1;i<=n*m;++i) if(!dfn[i]) dfs(i);
	if(tot==1) {cout<<"0\n";return 0;}//特判
	for(int u=1;u<=n*m;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			++in[col[v]],++out[col[u]];
		}
	}
	int res1=0,res2=0;
	for(int i=1;i<=tot;++i) res1+=(!in[i]),res2+=(!out[i]);
	cout<<max(res1,res2)<<"\n";
	return 0;
}

P7251 [JSOI2014] 强连通图

真是经典的trick，可以拿出来考一辈子。

第一问说明的就是一个 SCC 的性质，那么要求找出最大的点的集合，明显就是找出原图中最大的 SCC 大小。

第二问就和上道题一模一样，添加最少的边使得原图化作一个强连通图，找缩点之后 SCC 出度为 0 的点数和入度为 0 的点数最大值。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#include<bitset>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=3e5+5;
int n,m,num,tot,res1,res2,ans;
int dfn[M],low[M],col[M],in[M],out[M],siz[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		int x;++tot;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0,++siz[tot];
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]);
			++in[col[v]],++out[col[u]];
		}
	}
	for(int i=1;i<=tot;++i)
	{
		ans=max(ans,siz[i]);//第一问找强连通分量最大值
		res1+=(!in[i]),res2+=(!out[i]);
	}
	cout<<ans<<"\n";
	if(tot==1) cout<<"0\n";//特判原图为强连通分量
	else cout<<max(res1,res2)<<"\n";
	return 0;
}

P2272 [ZJOI2007] 最大半连通子图

批话题。一张有向图上，我们定义半连通子图为对于这个子图内的任意两点 \(u,v\)，至少存在一条路径 \(u \to v\) 或 \(v \to u\)，问你这张有向图的极大半连通子图大小。

看得出来，半连通的定义比强连通要宽松许多，强连通的定义应该是半连通的一个子集，双方是包含关系。于是缩点之后的每一个 SCC 肯定都是原图中的一个半连通子图。思考两者差别，显然强连通需要两个点互相到达，而半连通只需要其中一个点到达另一个点即可。

那么是不是我们从任一一个点出发，到达任一一个点结束，路径上经过的所有点+它们所在的 SCC 的所有点就应该也是原图的一个半连通子图。所以问题就转化为点有点权（实质上就是这个 SCC 的大小），找一条路径使得路径上所有点的点权和最大，成功转化为板子题。

而第二问自然就是最大权值路径数，这个可以跟着转移，设 \(f_u,x_u\) 分别为以 \(u\) 为结尾的路径点权最大值与点权最大值的路径数，对于边 \(u \to v\)，就有转移 \(f_v=max(f_v,f_u+siz_v)\) ，\(siz_v\) 是 \(v\) 这个 SCC 的大小。在 \(f_u+siz_v>f_v\) 时 \(x_v=x_u\)，在 \(f_u+siz_v=f_v\) 时，\(x_v+=x_u\)。初始化 \(f_i=siz_i,x_i=1\)。理解起来就是当前从 \(u\) 过来的路径权值最大，那么 \(v\) 最大权值路径数就是到达 \(u\) 最大权值路径数；而如果相等，那么 \(v\) 之前最大权值路径数保留，再加上到达 \(u\) 最大权值路径数。

由于这道题对于边敏感，如果你有重边的话，\(x_v\) 不就可能加上很多次 \(x_u\) 了？所以需要去掉重边。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
#include<map>
#define pii pair<int,int>
#define mk make_pair
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m,mod,tot,num;
int dfn[M],low[M],col[M],siz[M],in[M],f[M],x[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;
map<pii,int> mapp;

int cnt=0;
struct N{
	int to,next;
}; N p[M*10];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,++siz[tot];
			vis[x]=0;
			s.pop();
			if(u==x) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>mod;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]||mapp[mk(col[u],col[v])]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
			mapp[mk(col[u],col[v])]=1;//对已经出现的边做标记，方便判断。
		}
	}
	for(int i=1;i<=tot;++i)
	{
		f[i]=siz[i],x[i]=1;
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			if(f[v]<f[u]+siz[v])
			{
				f[v]=f[u]+siz[v],x[v]=x[u];
			}
			else if(f[v]==f[u]+siz[v])
			{
				f[v]=f[u]+siz[v],x[v]=(x[u]+x[v])%mod;
			}
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0,sum=0;
	for(int i=1;i<=n;++i)
	{
		if(ans<f[i]) ans=f[i],sum=x[i];
		else if(ans==f[i]) sum+=x[i];//答案统计同转移逻辑
	}
	cout<<ans<<"\n"<<sum%mod<<"\n";//注意取模
	return 0;
}

CF1027D Mouse Hunt

偏向考察 DAG 图性质的问题。一张有向图，有一个点可以随意移动，你可以选择一些点使其成为终点，但是选择每个点都是由代价的。问你最少需要耗费多大的代价才能使得这个点从任意位置开始移动都有可能到达终点。

首先考虑一个点能去那些地方，由于图是一张 DAG，所以从任意一个点 \(u\) 开始，它只能到达它所在的 SCC 内的点，和缩点之后 SCC 所能到达的 SCC 内的所有点。于是对于每一个 SCC ，只需要在里面有一个点被确立为终点，那么从这个 SCC 内的点出发都有可能到达终点。再要求代价最小的情况下显然选择 SCC 内点权最小的最优。

但是 \(u\) 还能到达缩点后 SCC 所能到达的 SCC 内的所有点，没有必要对每一个 SCC 内都设一个终点。那么我们需要选出一个点集使得每个点都可以到达这个点集内的点，什么时候点集最优？自然是选择所有出度为 0 的点。在出度为 0 的 SCC 选择其权值最小的点作为终点就是答案。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,num,tot,ans;
int dfn[M],low[M],col[M],minn[M],in[M],c[M];
bool vis[M];
stack<int> s;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v]) dfs(v),low[u]=min(low[u],low[v]);
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			minn[tot]=min(minn[tot],c[x]);// SCC 内权值最小点
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>c[i],minn[i]=2e9;
	for(int i=1,x;i<=n;i++) cin>>x,add(i,x);
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			++in[col[u]];//这里相当于统计的就是出度了
		}
	}
	for(int i=1;i<=tot;i++) if(!in[i]) ans+=minn[i];
	cout<<ans<<"\n";
	return 0;
}

CF999E Reachability from the Capital

考察 DAG 的性质。对于一张有向图，给定一个点 \(s\) 为首都，你可以在任意两个点间连无向边，问从首都可以到达所有城市所需的最少新修边数。

首先 SCC 内的点肯定都可以互相到达，所以缩点后考虑 DAG 应该怎么做。肯定从 \(s\) 所在的 SCC 出发能到达的 SCC 就不用个考虑了，这些一开始就能被到达。

那么对于没有被标记的 SCC 明显每个只要连一条边就可以和 \(s\) 连通了，但是没有被标记的 SCC 之间也可能存在有向边。问题转化为对于一张 DAG ，选择尽量少的点作为起点，可以到达任意一个点，经典套路，只需要选择入度为 0 的点即可。

所以本题答案就是出去能被起点到达的其余 SCC 入度为 0 的点的个数（话说都能被起点到达了 SCC 入度肯定就不为0了，应该是除开 \(s\) 所在的 SCC，其余入度为 0 的SCC 个数）。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e3+5;
int n,m,S,num,tot,ans;
int dfn[M],low[M],col[M],in[M];
bool vis[M];
stack<int> s;
vector<int> e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v]) dfs(v),low[u]=min(low[u],low[v]);
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,vis[x]=0;
			s.pop();
			if(x==u) break;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>S;
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[u]].push_back(col[v]),++in[col[v]];
		}
	}
	//cout<<col[S]<<"!\n";
	q.push(col[S]),vis[col[S]]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			if(!vis[v]) q.push(v),vis[v]=1;
		}
	}
	for(int i=1;i<=tot;i++) ans+=(!vis[i]&&!in[i]);//一开始没法被到达&&入度为0（我是脑瘫，不用建图也可以做，见上面讲解的最后一句）
	cout<<ans<<"\n";
	return 0;
}

P3436 [POI2006] PRO-Professor Szu

除了坑点多，早该降蓝了，和 P4645 [COCI2006-2007#3] BICIKLI 挺像的。一张有向图上给定终点，询问每个点到终点的路径数。

这很模板，显然在一个 \(siz>1\) 的 SCC 里可以绕一辈子，那么缩点后做 DAG 路径计数的同时，统计一下到达终点的路径上是否可能出现 \(siz>1\) 的 SCC。由于求到达到达终点的路径上的信息，所以建反图。

有一些细节注意一下。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e6+5;
int n,m,num,tot,ans;
int dfn[M],low[M],col[M],in[M],f[M],flag[M];
bool vis[M];
stack<int> s;
vector<int> e[M],bel[M],t;
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void tarjan(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		col[u]=++tot;
		while(s.top()!=u)
		{
			bel[tot].push_back(s.top());//由于后门询问需要针对每个点，那就把每个 SCC 内的点统计下来
			col[s.top()]=tot,vis[s.top()]=0;
			s.pop();
		}
		bel[tot].push_back(u),flag[tot]=(bel[tot].size()>1);
		s.pop(),vis[u]=0;
		for(int i=head[u];i!=0;i=p[i].next)//还有一种可以走很多次的可能是出现自环，当然可以在一开始判
		{
			int v=p[i].to;
			if(v==u) {flag[tot]=1;break;}
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n+1;i++) if(!dfn[i]) tarjan(i);
	for(int u=1;u<=n+1;u++)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			e[col[v]].push_back(col[u]);
			++in[col[u]];
		}
	}
	f[col[n+1]]=1,vis[col[n+1]]=1;
	for(int i=tot;i>=1;--i)
	{
		if(flag[i]) f[i]=36501;
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int v:e[u])
		{
			if(vis[u])
			{
				f[v]+=f[u],f[v]=min(f[v],36501);
				vis[v]|=vis[u];
			}
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=tot;i++)
	{
		if(!vis[i]) continue;
		if(f[i]>ans)
		{
			t.clear(),ans=f[i];
			for(int it:bel[i]) if(it!=n+1) t.push_back(it);
		}
		else if(f[i]==ans)
		{
			for(int it:bel[i]) if(it!=n+1) t.push_back(it);
		}
	}
	sort(t.begin(),t.end());
	if(ans>36500) cout<<"zawsze\n";
	else cout<<ans<<"\n";
	cout<<t.size()<<"\n";
	for(int it:t) cout<<it<<" ";
	return 0;
}

P5008 [yLOI2018] 锦鲤抄

也是较水的一道题，好评在简化版题意看着很爽。简化版题意：给你一张有向图，每个点有一个点权。任意时刻你可以任意选择一个有入度的点，获得它的点权并把它和它的出边从图上删去。最多能选择 \(k\) 个点，求最多能获得多少点权。

先不考虑 \(k\) 的限制，判断每个点是否能删。只能删有入度的点，那么考虑强连通的性质，两两之间都连通，那么对于一个 SCC，一定存在一种方案使得 SCC 被删的只剩下一个点；再思考有入度的 SCC，那么这个 SCC 内的点一定能全部被删完；最后如果一个 SCC 拥有自环的话，那么这个 SCC 内的点也一定能被删完。

相当于一个点可能不被删，当且仅当其所在的 SCC 没有入度&&没有自环。对于这样的 SCC，贪心的想，由于想要使得最后删去的点的点权和最大，那么钦定这个 SCC 内点权最小的一个点不被删。

那么题目做法就清晰了，对原图缩点建 DAG 之后，对于有入度或自环的 SCC，把 SCC 内的所有点拿出来，两个都没有的 SCC，把除去 SCC 其中点权最小的一个点，其余的点全部拿出来。排序后取出前 \(k\) 大的点就是要删的点了。

代码实现也比较简单：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack> 
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+15,N=2e6+15;
int n,m,k,num,tot,ans;
int dfn[M],low[M],in[M],col[M],w[M];
bool vis[M],c[M],flag[M];
stack<int> s;
vector<int> t[M],res;

int cnt=0;
struct edge{
	int to,next;
};edge p[N];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline bool cmp(int x,int y){return x>y;}
inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		++tot;int x;
		while(1)
		{
			col[(x=s.top())]=tot,t[tot].push_back(w[x]);
			vis[x]=0,flag[tot]|=c[x];
			s.pop();
			if(u==x) break;
		}
		sort(t[tot].begin(),t[tot].end(),cmp);//t是每一个 SCC 内的点的点权集合，可以先处理出来。
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>k;
	if(k==0) {cout<<"0\n";return 0;}
	for(int i=1;i<=n;++i) cin>>w[i];
	for(int i=1,a,b;i<=m;++i)
	{
		cin>>a>>b;
		if(a==b) c[a]=1;
		else add(a,b);
	}
	for(int i=1;i<=n;++i) if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(col[u]==col[v]) continue;
			++in[col[v]];
		}
	}
	for(int i=1;i<=tot;++i)
	{
		if(in[i]||flag[i])
		{
			for(auto it:t[i]) res.push_back(it);//全部加进去
		}
		else
		{
			for(int it=0;it<t[i].size()-1;++it) res.push_back(t[i][it]);//除了最小的那个其他的加进去
		}
	}
	sort(res.begin(),res.end(),cmp);
	for(int i=0;i<res.size();++i)//取前k个，当然也有可能能去的不足k个，但不影响
	{
		ans+=res[i],--k;
		if(!k) break;
	}
	cout<<ans<<"\n";
	return 0;
}