拓扑排序学习笔记

图论系列：

前言：

ぽつり夕立を食らった
此処に帰る傘はないんだ
ふたりで嵐を待った
どこへ行こうか 探してんだ

相关题单：戳我

一.图论基本定义

其实可以查oi wiki 的。

1.图

图：图是一个二元组 \(G=(V(G),E(G))\) ，其中 \(V(G)\) 是非空点集，由图的各个顶点组成，\(E(G)\) 是各点之间的边组成的边集。可以记 \(G=(V,E)\) 。

有向图：\(E\) 中每条边 \(e\) 都是有方向的。

无向图：\(E\) 中每条边 \(e\) 都是没有方向的。

混合图：\(E\) 中既有有方向的边，也有没有方向的边。

阶：图 \(G\) 的点数 \(V\) 称为阶，记作 \(|G|\)。

2.相邻

相邻：在无向图中，称 \(u,v\) 相邻当且仅当存在 \(e=(u,v)\)。

领域：在无向图中，所有与 \(u\) 相邻的点的集合，记作 \(N(u)\)。

3.简单图

自环：对于 \(E\) 中的边 \(e(u,v)\)，若 \(u=v\)，那么 \(e\) 被称作一个自环。

重边：若 \(E\) 中存在两个完全相同的元素 \(e1,e2\) ，则他们被称作重边。

简单图：图中不存在自环或重边。

4.度数

出边 / 入边：在有向图中，从 \(u\) 出发的边 \(u \to v\) 称为 \(u\) 的出边，到达u的边 \(v \to u\) 称为 \(u\) 的入边。

度数：一个点的度数就是与之关联的边的数量，记作 \(d(u)\) 。点的自环对其度数产生2的贡献。

出度 / 入度：从 \(u\) 出发的边的个数称作 \(u\) 的出度，到达 \(u\) 的边的个数称作 \(u\) 的入度。

5.路径

途径：途径是连接一连串顶点的边的序列，可以为有限或无限长度。一条有限途径 \(w\) 是一个边的序列 \(e_1,e_2,e_3......e_k\)，并且连接了一串点的序列 \(v_0,v_1,v_2.....v_k\)。

迹：对于一条途径 \(w\) 若 \(e_1,e_2,e_3......e_k\) 两两不相同，那么 \(w\) 是一条迹。

路径：对于一条迹，其连接的点的序列两两不相同，则称 \(w\) 是一条路径。

回路：对于一条迹，若 \(v_0=v_k\)，则称 \(w\) 是一条回路。

环/圈：对于一条回路 \(w\) ，若 \(v_0=v_k\) 是点序列中唯一重复出现的点对，那么 \(w\) 是一个环。

6.子图

实际上就是一个图的子集，只要对于两个图，\(G1=(E1,V1),G2=(E2,V2)\)，有 \(E2 \subseteq E1,V2 \subseteq V1\)，那么就称 \(G2\) 是 \(G1\) 的一个子图。

7.连通

连通：对于无向图的两点 \(u,v\)，若存在途径使得 \(v_0=u,v_k=v\)，则称 \(u,v\) 连通。

弱连通：对于有向图的两点 \(u,v\)，将有向边改为无向边后两点连通，则称 \(u,v\) 弱连通。

连通图：任意两点连通的无向图称为连通图。

弱连通图：任意两点弱连通的有向图称为弱连通图。

可达：有向图中的连通，存在一条途径使得 \(u\) 可以到达 \(v\)。

8.特殊图

简单图：图中不存在自环或重边。

有点无环图：简称DAG，不含环的有向图。

完全图：任意两点间都存在一条边。

树：\(|V|=|E|+1\)，并且保证所有点连通。

二.拓扑排序二.拓扑排序

1.操作流程

拓扑排序是对DAG（有向无环图）上的节点进行排序，使得对于每一条有向边 \(u \to v\)，\(u\) 都在 \(v\) 之前出现。简单地说，是在不破坏节点先后顺序的前提下，把DAG拉成一条链，使得排在前面的节点不能依赖于排在后面的节点。

操作也非常简单，一开始将所有点的入度统计出来，然后将入度为0的点存入队列中（使用队列是因为方便，一开始入度为0说明这些点都没有前置节点）。不断将点 \(u\) 从队列中取出来，消除自己出边的限制，然后判断当前出边到达的点 \(v\)，是否在这个出边消除之后入度就为0了，如果为0就也加入队列。

这样每个点都会进入和弹出队列一次，每一条边也只会被遍历一次，时间复杂度 \(O(n+m)\)。

随便造一张图来说明。

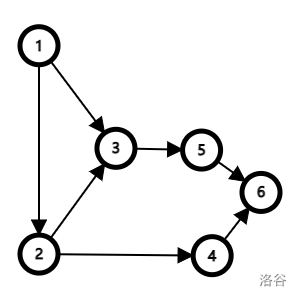
一开始统计各个点的入度，得到in数组应该是 \([0,1,2,1,1,2]\)。然后发现只有节点1的入度为0。

那么将点1放入队列，当前队头也就是1了，取出后弹出。发现其有两条出边 \((1,2)\) 与 \((1,3)\) ，消除限制之后，点2的入度变为0，点3的入度变为1。

将2放入队列，两条出边 \((2,3)\) 与 \((2,4)\)，消除限制之后，点3与点4的入度都变为0，然后3，4都放入队列。

从3消除，5入度归为0，放入5，从4消除，6入度变为1，最后消除5，6入读变为0，放入6后无法继续拓展了，排序过程结束。

整个图的拓扑排序实际上就是队列中点取出来的顺序，即 \([1,2,3,4,5,6]\)。（当然了，一张有向图的拓扑排序不唯一，这张图的拓扑排序还有可能是 \([1,2,4,3,5,6]\)）。

模板题代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=105;
int n;
int in[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
};N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];//统计入度
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,x;i<=n;i++)
	{
		while(1)
		{
			cin>>x;
			if(!x) break;
			add(i,x);
		}
	}
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);//加入入度为0的点
	while(!q.empty())
	{
		int u=q.front();
		cout<<u<<" ";
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v);//消除当前边的限制，如果消除后入度为0，加入队列
		}
	}
	return 0;
}

2.常见用法：

多见于各类建图题或图论类型的构造题

（1）拓扑序上DP

• DAG最长路：设 \(f_i\) 表示以 \(i\) 结尾的最长路径长度，\(f_v=max(f_v,f_u+1)\)。

• DAG 路径计数：设 \(f_i\) 表示以 \(i\) 结尾的路径数，\(f_v+=f_u\)。

• 点对可达性统计：设 \(f_{i,j}\) 表示 \(i\) 是否可以到达 \(j\) ，用bitset优化。

（2）最小 / 最大字典序拓扑序：

• 把queue换成大根堆/小根堆即可。

（3）结合强连通分量缩点

解决某些图上问题。（实际上大半还是跑DP）

3.习题

B3644 【模板】拓扑排序 / 家谱树

板子题，代码已经给出了。

P3074 [USACO13FEB] Milk Scheduling S

拓扑排序常见题型，根据题目给出的限制条件，需要在给奶牛B挤奶前结束给奶牛A的挤奶，设 \(f_i\) 是编号为 \(i\) 的奶牛最快完成挤奶的时间，\(t_i\)是 \(i\) 号奶牛需要挤奶的时间，那么转化为限制，\(f_b \geq f_a + t_b\)。

对于不存在限制的奶牛 \(f_i\) 自然等于 \(t_i\)，而对于存在限制的奶牛 \(u\)，就是所有指向自己的点的 \(f\) 数组最大值 + \(t_u\)，转移在拓扑的时候同时进行就可以了。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m;
int a[M],in[M],dis[M];
queue<int> q;
int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1,u,v;i<=m;i++) cin>>u>>v,add(u,v),++in[v];
	for(int i=1;i<=n;i++) if(!in[i]) dis[i]=a[i],q.push(i); //塞入入度为0的点，同时初始化这些点的f数组（dis数组）
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v],dis[v]=max(dis[v],dis[u]+a[v]);//要满足所有的限制，那么就只能取所有限制的max
			if(!in[v]) q.push(v);
		}
	}
	int maxx=0;
	for(int i=1;i<=n;i++) maxx=max(maxx,dis[i]);
	cout<<maxx<<"\n";
	return 0;
}

双倍经验： P1113 杂务

P4017 最大食物链计数

这个就是 DAG 路径计数板子题，建图时被吃者向吃者连边，设 \(f_i\) 表示以i结尾的路径数，初始化所有入度为0的点 \(u\) 使 \(f_u=1\)。

需要注意的是，题目要求的是最大食物链的数量，最左端生产者就是入度为0的点，那么最右端消费者就是出度为0的点，统计出度为0的点就是答案了。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#define int long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5,mod=80112002;
int n,m,ans;
int in[M],out[M],t[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++)
	{
		cin>>a>>b;
		add(b,a),++out[b],++in[a];//最后统计答案的时候需要用到出度
	}
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i),t[i]=1;//初始化f数组（也就是这里的t数组）
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			t[v]=(t[v]+t[u])%mod,--in[v];//按式子转移即可
			if(!in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++) if(!out[i]) ans=(ans+t[i])%mod;//统计答案
	cout<<ans<<"\n"; 
	return 0;
}

P6145 [USACO20FEB] Timeline G

实际上可以用差分约束求解（后面可能会写吧），使用拓扑的话实际上和第二题没有本质上的去别，他已经限制了所有点开始的最早&最晚时间，但最晚时间没有任何用（他给定了最后是存在一组解的）。

那么一开始初始化 \(f_i\) 为它限定的最早值 \(a_i\)，不一样的是这道题拥有边权，不像第二题这边刚结束另一边就可以开始，所以在建边的时候记录边权，最后转移的时候统计的就是 \(f_u+p_{i}.val\) 的最大值了。（但是我没这样写，我新建了一个点 \(S\)，作为一个超级源点，钦定 \(f_S=0\)，然后从 \(S\) 向每个点连一条边权为 \(a_i\) 的边，实际上作用是一样的）。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m,s,c;
int in[M],dis[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>c,s=n+1;//超级源点
	for(int i=1,x;i<=n;i++) cin>>x,add(s,i,x);
	for(int i=1,a,b,x;i<=c;i++) cin>>a>>b>>x,add(a,b,x);
	q.push(s);//一开始只用扔源点进去就可以力
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v],dis[v]=max(dis[u]+p[i].val,dis[v]);//这里转移的就是加上边权的最大值了
			if(!in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++) cout<<dis[i]<<"\n";
	return 0;
}

P1807 最长路

求DAG最长路的板子题，设 \(f_i\) 表示以 \(i\) 结尾的最长路径长度，对于每一个有边连向 \(v\) 的点 \(u\) 有 \(f_v=max(f_v,f_u+p_i.val)\)。直接跑就可以了。

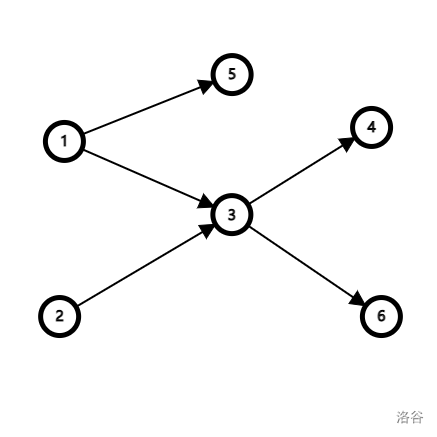
这里其实还有一个坑点，有些时候给定了起点，那么我们很有可能没法将所有入度为0的点放入队列中，这个时候一开始就要将非起点的入度为0的点的限制消掉，否则有些点的入度一直不为0，影响转移和最后的答案。

例如下列图中，我们指定1为起点，那么2的入度实际上也为0，但它已经没有可能进入队列了，于是它所限制的点3入度不可能消成0，接着点4和点6也会被影响。所以我们先将非起点的入度为0的点加入队列中先跑一遍拓扑排序，然后再加入起点跑拓扑就不会受到影响了，这种情况在很多限制起点的拓扑排序题会用到。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#define int long long  
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5,inf=1e18;
int n,m;
int in[M],dis[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	memset(dis,-0x3f,sizeof(dis));
	cin>>n>>m;
	for(int i=1,a,b,c;i<=m;i++)
	{
		cin>>a>>b>>c;
		add(a,b,c);
	}
	for(int i=2;i<=n;i++) if(!in[i]) q.push(i);//由于1是起点嘛，所以找其他的入度为0的点
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v];
			if(!in[v]&&v!=1) q.push(v);//差点就要祸害后人了，这里消除其他入度为0的点的影响的时候，不能把起点的影响消了
		}
	}
	q.push(1),dis[1]=0;//然后单独加入起点就可以了
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			dis[v]=max(dis[v],dis[u]+p[i].val),--in[v];
			if(!in[v]) q.push(v);
		}
	}
	if(dis[n]<-inf) cout<<"-1\n";
	else cout<<dis[n]<<"\n";
	return 0;
}

P2712 摄像头

挺板的，照着输入要求建出有向图后跑拓扑排序，看那些点的入度可以被消成0，入度最后可以消成0的那么就有办法砸了。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e4+5;
int n,res;
int in[M];
vector<int> pos[M],e[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,x,m;i<=n;i++)
	{
		cin>>x>>m;
		pos[x].push_back(i);
		for(int j=1;j<=m;j++) cin>>x,e[i].push_back(x);
	}
	for(int i=1;i<=n;i++)
	{
		for(int it:e[i]) for(int v:pos[it]) add(i,v);
	}
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();++res;//统计入度为0的点数
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v];
			if(!in[v]) q.push(v);
		}
	}
	if(res==n) {cout<<"YES\n";}
	else cout<<n-res<<"\n";
	return 0;
}

P8893 「UOI-R1」智能推荐

稍微具有转化的题，对于第 \(i\) 道题，当且仅当你把 \(s_i\) 中每一道题都做出来并且其中有一道题是当天做的，第二天就可以被推荐，其实是废话，有向图建出来后，你肯定要把前面所有的限制全部消除，并且对于一道题，设其能最早做完的时间为 \(f_i\) 就又转化为第二题了。把第一天推荐的题压入队列后，跑拓扑排序即可。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e6+5;
int n,k,m,q,maxx;
int in[M],dis[M],t[M];
queue<int> que;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>k>>m;
	for(int i=1,x;i<=m;i++) cin>>x,que.push(x),dis[x]=1;
	cin>>q;
	for(int i=1,x,siz,y;i<=q;i++)
	{
		cin>>x>>siz;
		for(int j=1;j<=siz;j++) cin>>y,add(y,x);
	}
	while(!que.empty())
	{
		int u=que.front();
		que.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			dis[v]=max(dis[u]+1,dis[v]),--in[v];
			if(!in[v]) que.push(v); 
		}
	}
	if(!dis[k]) cout<<"-1\n";
	else cout<<dis[k]-1<<"\n";//由于开始时间是第0天，我初始化的第1天（方便判断题目有无可能北座），所以-1
	return 0;
}

P10287 [GESP样题 七级] 最长不下降子序列

拓扑上DP，注意到 \(a_i\) 的值很小 \([1,10]\) 所以我们可以设 \(f_{i,j}\) 为对于点 \(i\) ，结尾为 \(j\) 的最长路径长度（注意题目并不需要连续路径，所以直接一维转移是错的┭┮﹏┭┮），那么初始化 \(f_{i,c_i}=1\) 跑拓扑排序。

还是设当前由点 \(u\) 转移到点 \(v\)。在\(1 \leq j \leq c_v\) 时，由于最长不下降嘛，\(f_{v,c_v}=max(f{u,j}+1,f_{v,c_v})\)，再从\(1 \leq j \leq 10\)，转移上一个点的最大值，\(f_{v,j}=max(f{u,j},f_{v,j})\) 。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m,ans;
int c[M],in[M],f[M][15];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>c[i];
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;i++)
	{
		if(!in[i]) q.push(i),f[i][c[i]]=1;//初始化
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			for(int j=1;j<=c[v];j++) f[v][c[v]]=max(f[u][j]+1,f[v][c[v]]);
			for(int j=1;j<=10;j++) f[v][j]=max(f[u][j],f[v][j]);//转移式见上
			--in[v];
			if(!in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=c[i];j++) ans=max(ans,f[i][j]);//找出最大值
	}
	cout<<ans<<"\n"; 
	return 0;
}

P10480 可达性统计

点对可达性统计板子题，设 \(f_{i,j}\) 表示 \(i\) 是否可以到达 \(j\) ，对于一条 \((u,v)\) 的有向边，有 \(f_{v,j}=f{v,j}|f_{u,j}\)。使用bitset硬性 \(O(n*m/w)\) 转移即可。

贴一个bitset的使用方法 https://www.cnblogs.com/magisk/p/8809922.html

好像还有一个问题，由于统计的时当前点可以到达的点的个数，不是这个点能被多少个点到达。所以我们建反图就可以了，对于一条边 \((u,v)\) ，建边时建成 \((v,u)\) 此时反图中跑出来的每个点被到达的点数不就是正图中可到达的点数力。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<bitset>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=3e4+5;
int n,m;
int in[M];
bitset<M> f[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) f[i][i]=1;//初始化
	for(int i=1,a,b;i<=m;i++) cin>>a>>b,add(b,a);//建反图，很多题都有这个trick
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			f[v]|=f[u];//bitset支持两个bitset类型快速各位操作
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++) cout<<f[i].count()<<"\n";//统计1的数量，就是可达点数
	return 0;
}

P1137 旅行计划

拓扑排序DP转移板子题，就是求以每个点结尾的最长路。

代码

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int n,m;
int in[100005],a[100005];
queue<int> q;
int cnt=0;
struct N{
	int to,next;
};N p[200010];
int head[100005];

inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

int main()
{
	cin>>n>>m;
	int x,y;
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y;
		add(x,y),in[y]++;
	}
	for(int i=1;i<=n;i++)
	{
		a[i]=1;
		if(!in[i]) q.push(i);
	}
	while(q.size()>0)
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			a[v]=max(a[u]+1,a[v]);
			in[v]--;
			if(!in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++) cout<<a[i]<<endl;
	return 0;
}//古早代码\se

AT_abc315_e [ABC315E] Prerequisites

有点意思，每一本书都有自己的前置书目，现在求读编号为1的书之前必须要读的书。

分享一些错误思路：

每本书前置书目向本书连边，直到1入度为0时前面所有的点都是要读的（明显有点问题啦，如果5是1的前置，2是3的前置，那么遍历到1之前可能2，3都遍历到了，发生错误）。

每一本书向自己的前置书目连边，遍历到1之后做一个标记，后面的那一串都是必须要读的。（也有一点问题，后面的某些书可能并不节制点1，画画图就看的出来）。

每一本书向自己的前置书目连边，那么为了不去节制点1的点都不被统计，我们可以拿一个大根堆来替代队列，这时候但凡有一个比1大的节点可以继续拓展那么1就一定不会被选出来，最后轮到1去拓展的点那么一定都是可以节制1的点，在1拿出来之后做一个标记，后面一串都是要读的。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,flag;
int in[M];
priority_queue<int> q;//大根堆
vector<int> res;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,k,x;i<=n;++i)
	{
		cin>>k;
		for(int j=1;j<=k;++j) cin>>x,add(i,x);//向前置书籍连边
	}
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.top();
		if(flag) res.push_back(u);//这些都是取出1之后取出来的，那么肯定节制1
		if(u==1) flag=1;//遍历到1就做标记
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=res.size()-1;i>=0;--i) cout<<res[i]<<" "; 
	return 0;
}

AT_abc291_e [ABC291E] Find Permutation

限制有点太宽松了，建边后跑一边拓扑排序，按照每个点的拓扑排序先后顺序进行赋权就可以了。

对于限制要求序列要唯一（也就是拓扑序唯一），肯定一开始要满足入度为0的点只有1个，并且每个点进行消除限制的时候，同时解封（入度变为0的点）一定小于等于1个。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,m,num;
int in[M],ans[M];
queue<int> q;
vector<int> res;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	if(q.size()>1) {cout<<"No\n";return 0;}//入度点为0的点超过1，pass
	while(!q.empty())
	{
		int u=q.front();num=0;
		res.push_back(u);//记录每一个点在拓扑序出现的先后顺序
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v),++num;
		}
		if(num>1) {cout<<"No\n";return 0;}//同时解封的超过1个，就不止1种拓扑序了
	}
	cout<<"Yes\n";
	for(int i=0;i<res.size();++i) ans[res[i]]=i+1;
	for(int i=1;i<=n;++i) cout<<ans[i]<<" ";
	return 0;
}

CF919D Substring

和前面 P10287 [GESP样题 七级] 最长不下降子序列 挺像的，那道题的权值就是这道题的字符集，把 \(f_{i,j}\) 设为 在点 \(i\)，所有到达其的路径中，出现字符为 \(j+'a'\) 的最大值。转移挺像的，见代码。（有自环输出-1）

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=3e5+5;
int n,m,ans;
int in[M],dp[M][27];
string s;
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>s,s=' '+s;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i)
	{
		if(!in[i]) q.push(i),++dp[i][s[i]-'a'];
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			for(int j=0;j<26;++j)
			{
				if(j==s[v]-'a') continue;
				dp[v][j]=max(dp[v][j],dp[u][j]);//转移上一个字符的最大值
			}
			dp[v][s[v]-'a']=max(dp[u][s[v]-'a']+1,dp[v][s[v]-'a']);//当前这个点代表字符就是上一个点这种字符出现次数最大值+1
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i) if(in[i]) {cout<<"-1\n";return 0;}//最后还有入度，说明有自环了，当然也可以一开始判
	for(int i=1;i<=n;++i)
	{
		for(int j=0;j<26;++j) ans=max(ans,dp[i][j]);//统计答案
	}
	cout<<ans<<"\n";
	return 0;
}

AT_abc223_d [ABC223D] Restricted Permutation

最小字典序拓扑序板子题，正常拓扑排序，将队列替换为小根堆，保证每一次进行转移的都是当前可以进行转移的编号最小的点。这样就保证了最后求出来的拓扑序的字典序最小。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,m;
int in[M];
priority_queue<int,vector<int>,greater<int>> q;//小根堆
vector<int> res;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.top();
		res.push_back(u);
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i)
	{
		if(in[i]) {cout<<"-1\n";return 0;}
	}
	for(int it:res) cout<<it<<" ";
	return 0;
}

P7113 [NOIP2020] 排水系统

属于是数学题了，有一张DAG，前面有若干个接受点会产生1吨废水，并且对于某个点 \(u\) 涌进来 \(x\) 吨废水，\(u\) 有 \(y\) 条出边，那么每条出边就会流 \(x/y\) 吨废水至下一个点，给定若干个排水点，废水流经排水点就没了，保证接受点的入度为0，排水点的出度为0。

还是比较好做的，一开始将所有接受点的权值赋为1，预处理每个点的出度 \(out_u\)，设 \(f_u\) 是流经 \(u\) 点的污水，那么对于边 \((u,v)\)，有 \(f_v=f_v+f_u/out_u\)，最后输出每个排水点的 \(f_i\)。

但是这题要求的是分数形式，所以我们可以使用 pair 类型来记录一个点的污水（可以记录下分子和分母），最后运算的时候使用分数加法就可以了，有一些小的细节。（最后分母可能太大，所以需要使用__int128类型才存的下）。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#define int __int128
#define pii pair<int,int>
#define mk make_pair
using namespace std;
inline void read(int &n){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    n=x*f;
}
inline void print(int n){
    if(n<0){
        putchar('-');
        n*=-1;
    }
    if(n>9) print(n/10);
    putchar(n % 10 + '0');
}//__in128没法使用常规的输入输出，需要手写快读快输
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5;
int n,m,g,s;
int in[M],out[M];
pii d[M];

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
queue<int> q;
inline void add(int a,int b)
{
	++cnt,++in[b],++out[a];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline pii solve(pii a,pii b)//分数加法
{
	g=__gcd(a.second,b.second),s=a.second*b.second/g;
	a.first*=s/a.second,b.first*=s/b.second;
	pii res=mk(a.first+b.first,s);
	g=__gcd(res.first,res.second);
	res.first/=g,res.second/=g;
	return res;
}
inline pii divide(pii a,int x)//分数除法
{
	g=__gcd(a.first,x);
	a.first/=g,x/=g,a.second*=x;
	return a;
}
signed main()
{
	
	read(n),read(m);
	for(int i=1;i<=m;++i) d[i]=mk(1,1);
	for(int i=m+1;i<=n;++i) d[i]=mk(0,1);//预处理，否则分母为0的话做除法和求gcd的时候会爆
	for(int i=1,k,x;i<=n;++i)
	{
		read(k);
		for(int j=1;j<=k;j++) read(x),add(i,x);
	}
	for(int i=1;i<=m;++i) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		pii res=divide(d[u],out[u]);
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v],d[v]=solve(d[v],res);
			if(!in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i)
	{
		if(!out[i])
		{
			print(d[i].first),cout<<" ",print(d[i].second),cout<<"\n";
		}
	}
	return 0;
}

P7860 [COCI2015-2016#2] ARTUR

由于 $ n \leq 5000$，所以我们可以 \(O(n^2)\) 的判断两个线段之间是否能互相影响，可以的话，就连一条有向边，最后跑拓扑排序就可以了，留作本章习题吧（写起来可能会有一点恼火）。

P4316 绿豆蛙的归宿

很牛的一道题，对于一张有边权的DAG，和 P7113 [NOIP2020] 排水系统 相似，每一个点有 \(x\) 条出边时有 \(1/x\) 的概率选择某一条边，给定起点 \(1\)，求最后到达终点 \(n\) 的期望路径长度。还是设 \(f_i\) 为点 \(i\) 到终点的期望路径长度，答案就是 \(f_1\)。

一般来说，对于DP初始状态确定时可用顺推，终止状态确定时可用逆推，正向进行拓扑后面的点根本没法影响到 \(f_1\)，那么考虑建反图，这时候就非常显然了，对于边 \((u,v)\)，\(f_v+=(f_u+p_i.val)/out_v\)，因为是逆推的，实际上是 \((v,u)\)，从 \(v\) 走到 \(u\) 的概率为 \(1/out_v\)，而 \(v\) 走到 \(u\) 之后期望路径长度是 \(f_u\) 加上 \(v \to u\) 这条边的长度，所以产生的贡献就是 \((f_u+p_i.val)/out_v\)，最后得到 \(f_1\)。（注意这里的出度指的是正图中的出度）

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m;
double ans,t[M];
int in[M],out[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
	double val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,double c)
{
	++cnt,++in[b],++out[b];//反图的入度=正图的出度
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	double c;for(int i=1,a,b;i<=m;i++) cin>>a>>b>>c,add(b,a,c);//建反图
	q.push(n);//实际上这里应该消除非起点的入度为0的点的限制
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v];
			t[v]+=(t[u]+p[i].val)/out[v];
			if(!in[v]) q.push(v);
		}
	}
	printf("%.2lf\n",t[1]);
	return 0;
}

P6154 游走

启发性很大啊，和上一道题类似，但是它问的是所有路径的期望长度，起点与终点都任意。

已知所有路径的期望长度=所有路径的总长度/路径总数，前面已经提过路径总数的求法，现在需要求的就是所有路径的总长度，对于每一个点 \(i\)，设 \(f_i\) 为以 \(i\) 为终点的所有路径长度，\(t_i\) 为 \(i\) 为终点的路径数。

对于边 \((u,v)\) 有转移 \(t_v=t_v+t_u\)，\(f_v=f_v+f_u+t_u\)，路径数转移显然，路径总长度加上的是每一个可以到达 \(v\) 的 \(u\)，以 \(u\) 为终点的路径总长度+路径数（边权为1，每一种路径都可以延申1，总共就是 \(f_u+t_u\) ）之和。

由于没有规定起点和终点，总路径数就是 \(t_i\) 之和，路径总长度就是 \(f_i\) 之和。最后费马小定理求个逆元，转移的同时记得取模。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#define int long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e6+5,mod=998244353;
int n,m,ans,res;
int in[M],t[M],dis[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}

inline int quick(int a,int n)
{
	int res=1;
	while(n)
	{
		if(n&1) res=res*a%mod;
		a=a*a%mod,n>>=1;
	}
	return res;
}
inline int inv(int x){return quick(x,mod-2);}//费马小定理求逆元
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i)
	{
		t[i]=1;
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			t[v]=(t[v]+t[u])%mod,dis[v]=(dis[v]+dis[u]+t[u])%mod;//转移方程
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i) res=(res+t[i])%mod,ans=(ans+dis[i])%mod;//求和
	cout<<ans*inv(res)%mod<<"\n";
	return 0;
}

P1685 游览

和上面两道题相似，只不过给定了起点，加上了边权还有一个坐船需要时间，直接放代码了。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e4+5,mod=1e4;
int n,m,s,t,k;
int in[M],num[M],sum[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>s>>t>>k;
	for(int i=1,a,b,c;i<=m;i++) cin>>a>>b>>c,add(a,b,c);
	q.push(s),num[s]=1;//严谨一点，需要消除非1的入度为0的点的限制
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			--in[v],num[v]=(num[u]+num[v])%mod;//路径数转移
			sum[v]=(sum[v]+sum[u]+p[i].val*num[u])%mod;//总路径长度转移，有边权
			if(!in[v]) q.push(v);
		}
	}
	cout<<(sum[t]+(num[t]-1)*k)%mod<<"\n";//加的是坐船所需要的时间
	return 0;
}

P1038 [NOIP2003 提高组] 神经网络

说些批话不知道想表达啥，实际上就是在一个DAG中，边有边权每一个点有一个初始权值和一个给定的限制，并且给定了一些起点与终点，只有在点的权值超过限制的时候才会激活并对自己出边到达的点产生权值上的贡献，起点没有限制已经被激活，并且保证起点没有入边，终点没有出边，询问最后终点是否被激活。

挺板的，难点在理解题意了，直接根据题意建边，跑拓扑的时候判断当前点是否被激活，被激活就转移自己的贡献，嘴和按题意输出。

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#define int long long
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m,flag;
int c[M],in[M],out[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt,++in[b],++out[a];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,x;i<=n;++i)
	{
		cin>>c[i]>>x;
		if(c[i]) q.push(i);
		else c[i]-=x;//先减去限制，这样权值>0的时候说明这个点被激活了
	}
	for(int i=1,a,b,c;i<=m;++i) cin>>a>>b>>c,add(a,b,c);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(c[u]>0) c[v]+=p[i].val*c[u]; //被激活了就转移贡献
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i)
	{
		if(out[i]||c[i]<=0) continue;
		cout<<i<<" "<<c[i]<<"\n",flag=1;
	}
	if(!flag) cout<<"NULL\n";
	return 0;
}

P1347 排序

给定你 \(m\) 个条件 形如 \(a \leq b\) ，问你在给定多少个条件之后可以确定这 \(n\) 个元素的唯一顺序或存在矛盾，抑或是最后都没法判断。

注意到实际上 \(n,m\) 的范围很小，那么我们可以暴力的枚举当前拥有前 \(i\) 个条件时，是否可以判断唯一顺序或存在矛盾。

判断唯一顺序参照 [ABC291E] Find Permutation ，有矛盾嘛就是 \(in\)数组有没归0的

代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e3+5;
int n,m,num,flag;
int in[M];
bool vis[M];
string str[M];
queue<int> q;
vector<int> ans;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b],vis[a]=vis[b]=1;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline int check(int x)//暴力枚举前x个条件看有没有结果
{
	while(!q.empty()) q.pop();cnt=flag=0,ans.clear();//记得清空
	for(int i=1;i<=n;++i) head[i]=in[i]=vis[i]=0;
	for(int i=1;i<=x;++i) add(str[i][0]-'A'+1,str[i][2]-'A'+1);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();num=0;
		q.pop();
		ans.push_back(u);
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) ++num,q.push(v);
		}
		flag|=(num>1);
	}
	for(int i=1;i<=n;++i) if(vis[i]&&in[i]) return 0;//矛盾
	if(flag) return 1;//不唯一，不能判断
	for(int i=1;i<=n;++i) if(!vis[i]) return 1;//有没有出现的点
	return 2;//确定了顺序
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;++i) cin>>str[i];
	for(int i=1,opt;i<=m;++i)
	{
		opt=check(i);
		if(!opt)
		{
			cout<<"Inconsistency found after "<<i<<" relations.\n";
			return 0;
		}
		else if(opt==1) continue;
		else
		{
			cout<<"Sorted sequence determined after "<<i<<" relations: ";
			for(int it:ans) cout<<(char)(it+'A'-1);
			cout<<".\n";
			return 0;
		}
	}
	cout<<"Sorted sequence cannot be determined.\n";
	return 0;
}

CF510C Fox And Names

拓扑排序结合字典序，由于打乱了字典序之后给定了一车字典序由小到大的字符串，并且 \(n\) 很小，那么正常字典序判断就是一个一个的比直到发现第一个不一样的。借鉴这样的思路，我们就可以 \(O(n^2)\) 的枚举任意两个字符串，比较他们第一个不一样的地方，然后连边跑拓扑就可以了。最后跑出来的拓扑序就是字典序。

留作习题吧。（其实是我没写啦\ke）。

AT_nikkei2019_qual_d Restore the Tree

题目给定有向图中的所有边都是原树的一个节点连上了自己的后代节点，让我们输出一种原树结构。
建出图之后，考虑树的性质，每一个点一定只有一个父亲节点，那么为了方便，我们钦定将当前点入度消为0的那个点就是当前点的父亲，这样保证每个点只会拥有一个父亲，跑一遍拓扑。对于一开始入度为0的点，自然就是树的根了。（题目好像已经给定了一定存在这样的树，就不用判无解了）

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m;
int in[M],pre[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<n+m;++i) cin>>a>>b,add(a,b);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v),pre[v]=u;
		}
	}
	for(int i=1;i<=n;++i) cout<<pre[i]<<"\n";
	return 0;
}

AT_abc245_f [ABC245F] Endless Walk

板子题，在有向图中想一直走就只能是在环上，于是就变成了一道拓扑排序判环上的点，跑一边拓扑之后入度还没有消成0的就一定在环上了。统计有多少个这样的点即可。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e5+5;
int n,m;
int in[M];
queue<int> q;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(b,a);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v);
		}
	}
	int ans=0;
	for(int i=1;i<=n;++i) ans+=(in[i]!=0);
	cout<<ans<<"\n";
	return 0;
}

接下来的几道都有相同的转化方式，正难则反。

P3243 [HNOI2015] 菜肴制作

神题，注意到这道题要求的并不是字典序最小，而是尽快吃到质量高的菜肴。所以整理一下，这道题一共两个限制：

（1）\(m\) 对 形如 \((i,j)\) 的限制，表示在做第 \(j\) 道之前需要先做第 \(i\) 道。

（2）尽快吃到质量高的菜肴（也就是说保证1在最前面的同时2在最前面，以此类推）。

显然正图建出来之后不好去维护，那么我们考虑反图是否可以维护，贪心的想，为了让小的菜肴尽量靠前，那么大的菜肴就要尽量靠后，那么每一个菜肴都找到自己最靠后并且没有被占的地方，最后的1菜肴所处的位置就一定是它所能在的第一个位置。

所以现在就转化为让大的菜肴尽量靠后，那么就相当于在反图上跑一个最大字典序（反图拓扑序的第一个就是正图拓扑序的最后一个），正图中大的菜肴尽量靠后，反图中大的菜肴尽量靠前。就是求一个反图字典序最大的拓扑序，这个维护简单，使用一个大根堆做就可以了。（然后判下环之类的细节就没了）。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int T,n,m,flag;
int in[M];
priority_queue<int> q;
vector<int> res;

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>T;
	while(T--)
	{
		cin>>n>>m,cnt=flag=0,res.clear();
		for(int i=1;i<=n;++i) head[i]=in[i]=0;
		for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(b,a);
		for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
		while(!q.empty())
		{
			int u=q.top();q.pop();
			res.push_back(u);
			for(int i=head[u];i!=0;i=p[i].next)
			{
				int v=p[i].to;
				if(!--in[v]) q.push(v);
			}
		}
		for(int i=1;i<=n;++i)
		{
			if(in[i]) {cout<<"Impossible!\n",flag=1;break;}
		}
		//for(int i=1;i<=n;++i) cout<<in[i]<<" ";cout<<"?\n";
		if(flag) continue;
		for(int i=res.size()-1;i>=0;--i) cout<<res[i]<<" ";
		cout<<"\n";
	}
	return 0;
}

CF1765H Hospital Queue

和上面那道题其实挺像的，也是两个限制。编号为 \(i\) 的病人必须排在前 \(p_i\) 位，编号为 \(a_i\) 的病人必须排在编号为 \(b_i\) 的前面。

问，对于每一位病人，在所有合法的排队方案中，他能排在的最靠前的位置。由于需要求出每一位病人最靠前的位置，跑一遍拓扑似乎并没有什么用，考虑对每一个病人跑一遍拓扑，实际上就是上一道题把优先级最大调成当前求的这个人。

思路平移下来，建出反图之后，其他的点尽量往前放（当然限制1越大的点越早放，所以还需要使用大根堆维护，每次找出限制最大的那个点），直到自己非放不可的时候才放，就能保证自己在正图的拓扑序中出现位置尽量靠前。那么什么时候自己非放不可呢？

1. 已经没有点可填了

2. 不填他后面的就无法满足第一种限制了，取出来的已经是可以填的数限制1最大（宽松）的了，结果它还是不能放在当前枚举位置。

每个点都跑一遍拓扑找出自己反图中最靠后的位置就可以了。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e3+5;
int n,m;
int f[M],pre[M],in[M];
bool vis[M];
priority_queue<pair<int,int>> q;

int cnt=0;
struct N{
	int to,next;
};N p[M<<1];
struct edge{
	int a,b;
};edge e[M];
int head[M];
inline void add(int a,int b)
{
	++cnt,++pre[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void topu(int x)
{
	while(!q.empty()) q.pop();
	for(int i=1;i<=n;++i)
	{
		in[i]=pre[i];
		if(!in[i]&&i!=x) q.push(make_pair(f[i],i));
	}//每一次都需要重建图
	for(int i=n;i>=1;--i)//代表在正图中出现的位置
	{
		if(q.empty()||q.top().first<i) {cout<<i<<" ";break;}//当前位置没有点可以填了 或 当前还不填枚举点，当前将被填的点的限制1就不被满足
		int u=q.top().second;q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]&&v!=x) q.push(make_pair(f[v],v));
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>f[i];
	for(int i=1;i<=m;++i) cin>>e[i].a>>e[i].b,add(e[i].b,e[i].a);//建反图
	for(int i=1;i<=n;++i) topu(i);//每一个点
	return 0;
}

P1954 [NOI2010] 航空管制

上面的多倍经验，随便跑一组合法解就可以了

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e4+5;
int n,m;
int f[M],pre[M],in[M],res[M],a[M];
bool vis[M];

int cnt=0;
struct N{
	int to,next;
};N p[M<<1];
struct edge{
	int a,b;
};edge e[M];
int head[M];
inline bool cmp(int x,int y){return f[x]<f[y];}
inline void add(int a,int b)
{
	++cnt,++pre[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void topu(int x)
{
	priority_queue<pair<int,int>> q;
	for(int i=1;i<=n;++i)
	{
		in[i]=pre[i];
		if(!in[i]&&i!=x) q.push(make_pair(f[i],i));
	}
	for(int i=n;i>=1;--i)
	{
		if(q.empty()||q.top().first<i) {res[x]=i;break;}
		int u=q.top().second;q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]&&v!=x) q.push(make_pair(f[v],v));
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>f[i],a[i]=i;
	for(int i=1;i<=m;++i) cin>>e[i].a>>e[i].b,add(e[i].b,e[i].a);
	queue<int> q;
	for(int i=1;i<=n;++i)
	{
		in[i]=pre[i];
		if(!in[i]) q.push(i);
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			f[v]=min(f[v],f[u]-1);
			if(!--in[v]) q.push(v);
		}
	}//跑一组合法解
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;++i) topu(i);
	for(int i=1;i<=n;i++) cout<<a[i]<<" ";cout<<"\n";
	for(int i=1;i<=n;i++) cout<<res[i]<<" ";cout<<"\n";
	return 0;
}

AT_abc304_h [ABC304Ex] Constrained Topological Sort

和上面两道的形式差不多，先使用拓扑排序将每个点真实的 \(l_i,r_i\) 限制求出来，然后贪心的根据 \(r\) 从小到大考虑每个点，使每个点的拓扑序在满足要求的前提下尽可能小。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<set>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=4e5+5;
int n,m;
int in[M],ans[M];
queue<int> q;
vector<int> t[M];
set<int> s;
bool vis[M];

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
struct edge{
	int u,v;
};edge e[M];
struct node{
	int l,r,id;
	inline bool operator <(const node &o) const
	{
		return r<o.r;
	}
};node a[M];
int head[M];
inline void add(int a,int b)
{
	++cnt,++in[b];
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	//freopen("050 (1).txt","r",stdin);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>e[i].u>>e[i].v;
		add(e[i].u,e[i].v);
	}
	for(int i=1;i<=n;++i) cin>>a[i].l>>a[i].r,a[i].id=i;
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop(),vis[u]=1;
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i)
	{
		if(in[i]&&!vis[i]) {cout<<"No\n";return 0;}//判断无解
	}
	for(int i=1;i<=m;++i) ++in[e[i].v];
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			a[v].l=max(a[v].l,a[u].l+1);//真实的l限制
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;++i) head[i]=0;cnt=0;
	for(int i=1;i<=m;++i) add(e[i].v,e[i].u);
	for(int i=1;i<=n;++i) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=p[i].next)
		{
			int v=p[i].to;
			a[v].r=min(a[v].r,a[u].r-1);//真实的r限制
			if(!--in[v]) q.push(v);
		}
	}
	for(int i=1;i<=n;i++) t[a[i].r].push_back(i);
	for(int i=1;i<=n;i++)//贪心
	{
		s.insert(i);
		for(int it:t[i])
		{
			auto pos=s.lower_bound(a[it].l);
			if(pos==s.end()) {cout<<"No\n";return 0;}
			ans[it]=*pos,s.erase(pos);
		}
	}
	cout<<"Yes\n";
	for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
	return 0;
}

P7877 「SWTR-7」Spider Solitaire

大模拟题，有 \(1-n\)共\(n\)个数，从右往左如果是一个顺子的话就可以同时移动，并且需要保证这个顺子的最左边的数是移动到的牌堆最右端数小1（相当于连成了一个更长的顺子），询问将 \(m\) 个牌堆合成一个的最小步数，此外，你还需要对于每个数 \(i\)，输出如果要移动 \(i\) 至少需要多少步。

模拟，首先先把每个牌堆里从右往左的顺子全部合并成一个点（要求最小那肯定同时移动最优），然后在一个牌堆中的顺子每个向自己左边的那个顺子连一条有向边。

例如一个牌堆是 \(3,2,9,8,7,5,4\)，\(3,2\) 合成一个，\(9,8,7\) 合成一个，\(5,4\) 合成一个，\(5,4\)连向 \(9,8,7\) 连向 \(3,2\) ，这就类似于一种限制，你只有移动了 \(5,4\) 之后才有可能移动 \(9,8,7\)。

然后对于 \(1-n\) 相邻的两个数如 \(2,3\)，\(5,6\)，如果它们并没有归在同一个顺子中的话，\(i+1\) 所在的顺子就向 \(i\) 所在的顺子连边，因为你只有可能移动到那去。

有解当且仅当每一个都有可能被遍历到，且建出来的图是一个 DAG，那么拓扑排序盘就是了。

然后第二问要求移动一个数之前需要多少步，那么统计所有限制自己所在顺子的顺子，用一个bitset暴力统计就可以了。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<bitset>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e4+5;
int T,n,m,tot,ans=1;
int siz[M],fa[M],bel[M],pre[M],suf[M],in[M],res[M];
bitset<M> c[M];
vector<int> t[M],e[M],g[M];
bool vis[M],flag[M];

inline void dfs(int u)
{
	c[u][u]=1;
	for(int v:g[u])
	{
		if(!c[v][v]) dfs(v);
		c[u]|=c[v];
	}
}//统计限制自己的点数

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>T;
	cin>>n>>m;
	for(int i=1,x;i<=m;++i)
	{
		cin>>siz[i];
		for(int j=1;j<=siz[i];++j) cin>>x,t[i].push_back(x);
		t[i].push_back(0);
	}
	for(int i=1;i<=m;++i)
	{
		for(int j=siz[i]-1;j>=0;--j)
		{
			if(t[i][j]==1||t[i][j]!=t[i][j+1]+1) ++tot,fa[tot]=bel[t[i][j+1]];//顺子缩在一起
			bel[t[i][j]]=tot;
		}
	}
	for(int i=1;i<=tot;++i) e[fa[i]].push_back(i);//第一种边
	for(int i=1;i<n;++i) if(bel[i]!=bel[i+1]) pre[bel[i+1]]=bel[i],suf[bel[i]]=bel[i+1];//第二种边
	suf[bel[n]]=n+1;
	queue<int> q;
	q.push(0),vis[0]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		if(flag[u]) continue;
		flag[u]=1;
		for(int v:e[u])
		{
			vis[v]=1;
			if(vis[pre[v]]&&v) q.push(pre[v]);
			if(v&&vis[suf[v]]) q.push(v);
		}
	}
	for(int i=1;i<=tot;++i) if(i!=bel[n]) ans&=flag[i];
	if(ans) cout<<"YES\n"<<tot-1<<"\n"; 
	else cout<<"NO\n";
	for(int i=1;i<=tot;++i)
	{
		if(fa[i]) g[i].push_back(fa[i]),++in[fa[i]];
		if(fa[suf[i]]) g[i].push_back(fa[suf[i]]),++in[fa[suf[i]]];
	}
	for(int i=1;i<=tot;++i) if(!in[i]) dfs(i);
	for(int i=1;i<=tot;++i)
	{
		res[i]=(flag[i]?c[i].count():-1);
	}
	for(int i=1;i<=n;++i) cout<<res[bel[i]]<<"\n";
	return 0;
}